8.1.4.2. Вычислительные процедуры метода главных

компонент

Решение задачи методом главных компонент сводится к поэтапному преобразованию матрицы исходных данныхX:

где X – матрица исходных данных размерностью п × т; п – число объектов наблюдения; т – число элементарных аналитических признаков;

Z – матрица стандартизованных значений признаков, элементы матрицы вычисляют по формуле ;

R – матрица парных корреляций: R =1/nZZ'.

Если предварительная стандартизация данных не проводилась, то на данном шаге получают матрицу S=1/n ∙ XX'; элементыматрицы X для расчета S будут центрированными величинами: x_ij=x_ij –.

Λ – диагональная матрица собственных (характеристических) чисел:

_.

Множество значений λ_j находят решением характеристического уравнения |R–λE|= 0. λ_j – это характеристики вариации, точнее показатели дисперсии каждой главной компоненты. Суммарное значение равняется сумме дисперсий элементарных признаковX_j. При условии стандартизации исходных данных, когда D(z_ij)=1, равно числу элементарных признаков т.

Решение характеристического уравнения относительно λ, когда число признаков т достаточно велико и матрица R большой размерности, вызывает трудности при расчете определителя |R|. Они успешно преодолеваются с применением разнообразных математических методов матричной алгебры. Наиболее эффективен и легко поддается алгоритмизации среди них метод, базирующийся на рекуррентных соотношениях Фаддеева. Если А – некоторая симметрическая матрица размерностью т × т, то ее определитель находится по следу матриц, производных из А:

На заключительном этапе расчетов Р_т и есть определитель матрицы А (Р_т =|A|). Для проверки вычислений может использоваться условие В_т= 0. После вычислений рекуррентных соотношений записы-вается характеристический многочлен_.

Значения λ находят после того, как характеристический многочлен приравнивают нулю, получают характеристическое уравнение и решают его относительно характеристических корней λ_j.

V – матрица нормированных собственных (характеристических) векторов. Число векторов V_j первоначально равно т, т.е. j = 1,m.Получают V_j преобразованием ненормированных собственных векторов U:

,

где |U_j| – норма вектора U, т.е

Необходимость повторного, после получения матрицы Z, нормирования пространства теперь уже обобщенных признаков R^F объясняется механическим появлением в ходе предыдущих расчетов результатов, искажающих нормированное пространство.

В свою очередь, собственные векторы U_j находят из матричного уравнения (R–λE)U = 0. Реально это означает решение т систем линейных уравнений для каждого λ _j при .

В общем виде система уравнений имеет вид

Приведенная система объединяет однородные линейные уравнения, и, так как число ее уравнений равняется числу неизвестных, u_mj имеет бесконечное множество решений. Конкретные значения собственных векторов при этом можно найти, задавая произвольно по крайней мере величину одной компоненты каждого вектора, и обычно, чтобы не усложнять расчетов, ее приравнивают единице.

А – матрица факторного отображения, ее элементы а_ri – весовые коэффициенты. Вначале А имеет размерность т × т – по числу элементарных признаков X_j, затем в анализе остается r наиболее значащих компонент, r ≤ т . Вычисляют матрицу А по известным данным матрицы собственных чисел Λ и нормированных собственных векторов V по формуле^.

F – матрица значений главных компонент размерностью rп, или, или.

Матрица F в общем виде записывается:

Пример 8.1. Совокупность из четырех промышленных предприятий оценена по трем характерным признакам: выработке на одного среднегодового работника Х₁, уровню рентабельности Х₂ и уровню фондоотдачи X₃.

В результате предварительных аналитических расчетов по исходным данным X получена матрица парных корреляций

.

Используя алгоритм метода главных компонент, необходимо найти собственные числа и собственные векторы матрицы R и построить матрицы с аналитическими результатами (А и F)

1. По рекуррентным соотношениям Фаддеева вычислим определитель матрицы парных корреляций |R|.

Первый шаг:

R=A и A=A₁, тогда P₁=t_rA₁=1+1+1=3,

.

Второй шаг:

;

,

.

Третий шаг:

=;

.

В итоге |R| = 0,524 и В₃= 0. Обратим внимание, что в ходе расчетов все промежуточные матрицы A_j и B_j – симметрические.

2. Построим характеристическое уравнение

,

откуда

Таким образом, наши исходные элементарные признаки Х₁, Х₂, Х₃ могут быть обобщены значениями трех главных компонент, причем первая главная компонента F₁ объяснит примерно 60 % всей вариации X_j (1,798/3 = 0,599), вторая главная компонента F₂ объяснит 29,2 % – меньшую часть по сравнению с F₁ общей дисперсии (0,875/3 = 0,292), наконец, третья главная компонента F₃ охватывает оставшуюся, еще не объясненную вариацию входных признаков – 10,9 % (0,327/3= 0,109). Все главные компоненты F₁, F₂, F₃ объясняют вариацию Х₁, Х₂, Х₃ полностью, на 100 % (59,9 + 29,2 + 10,9).

Собственные векторы матрицы парных корреляций R найдем решением трех систем линейных уравнений соответственно для λ₁ = 1,798; λ₂ = 0,875 и λ₃= 0,327.

Для определения области решений в каждой системе будем задавать одному из неизвестных признаков и_3j значение, равное единице.

Первая система уравнений для λ₁ = 1,798:

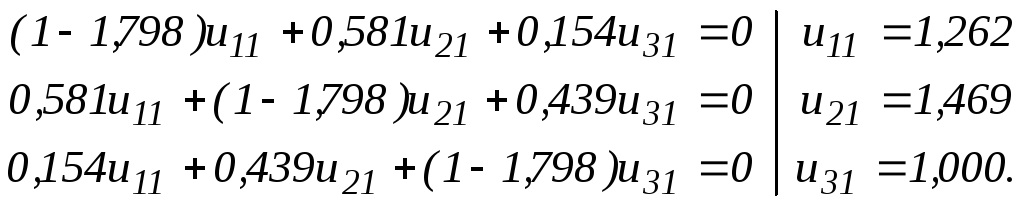
Вторая система уравнений для λ₂ = 0,875:

Третья система уравнений для λ₂ = 0,327:

Матрица собственных векторов принимает вид

.

Пронормируем векторы U_j, т.е. найдем V_j =U_j/|U_j| и получим матрицу нормированных значений собственных векторов

.

Так как V – матрица, отображающая ортонормированное пространство, в общем должно выполняться условие VV' = Е.

Матрицу факторного отображения (А) получим из матричного уравнения А = VΛ^1/2:

Матрица А содержит частные коэффициенты корреляции, представляющие связи исходных признаков X_j и главных компонент F_r. Соответственно все элементы а_ij могут варьировать в пределах от – 1 до +1. Из равенства А'А = Λ следует условие. Проверим,как оно выполняется на вычисленных данных матрицы А:

;

.

Теперь запишем системы линейных уравнений зависимости элементарных признаков Z_j и главных компонент или обобщенных признаков F_r при r =j = 3:

На завершающем шаге алгоритма вычислим значения главных компонент для всех наблюдаемых объектов и построим матрицу

F = A^–1Z', а матрица Z известна из условия задачи.

Более привычной формой записи п × r значений главных компонент является транспонированная матрица F:

Центр распределения значений главных компонентF_r находится в точке (0, 0, ..., 0), как это показано на рис. 8.9. Отсюда следует правило равенства суммы элементов каждого столбца матрицы F нулю. В примере это правило выдерживается.

Далее аналитические выводы по результатам расчетов следуют уже после принятия решения о числе значащих признаков Z_j и главных компонент F_r и определения названий главных компонент.