8.1.3. Общий алгоритм и теоретические

проблемы факторного анализа

Методы факторного анализа при всем их многообразии имеют общий алгоритм решения, представленный на рис.8.5. Начинаясь построением матрицы исходных данных X, этот алгоритм завершается получением матриц факторного отображения и значений факторов А и F. С учетом принятых обозначений, где п – число наблюдений; т – число аналитических признаков X; r – число значимых обобщенных признаков (латентных факторов), на схеме показана размерность матриц данных для каждого алгоритмического шага.

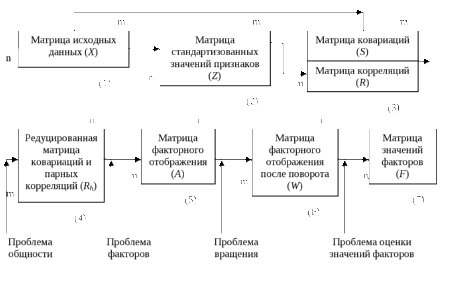
Рис. 8.5. Алгоритмическая схема реализации методов факторного анализа

Первые шаги алгоритма 1–3 не вызывают каких-либо затруднений. Переход от матрицы исходных данных X к матрице стандартизованных данных Z осуществляется после пересчета всех элементов x_ij по формуле z_ij=(x_ij –)ς_j. Как известно, для стандартизованных значений z_ij математическое ожидание (М (z) = 0) и дисперсия D (z) = 1. На следующем шаге простым перемножением скаляра 1/n и матриц Z' и Z получаем матрицу парных корреляций R = 1/nZ’Z. Шаг 2 может быть опущен, и тогда последующее факторное решение находят не по матрице R, а по матрице ковариаций S=1/nXX’, в последнем случае желательно, чтобы анализируемые признаки X имели одни и те же единицы измерения.

Выполнение четвертого шага алгоритма заключается в построении редуцированной матрицы корреляций (ковариаций). Проблема актуальна именно для методов факторного анализа, так как в методе главных компонент принимается, что всю вариацию исходных признаков полностью объясняют латентные факторы, при этом матрица парных корреляций R размерности т × т остается и как редуцированная R_h, в которой все общности

:

.

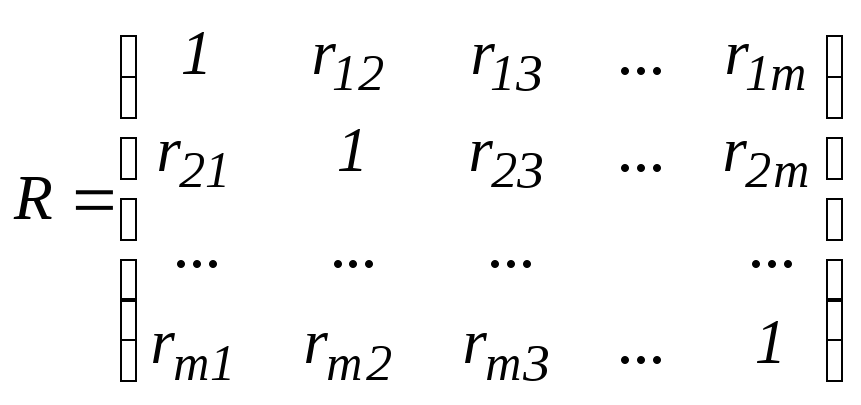В факторном анализе матрица корреляций R преобразуется в

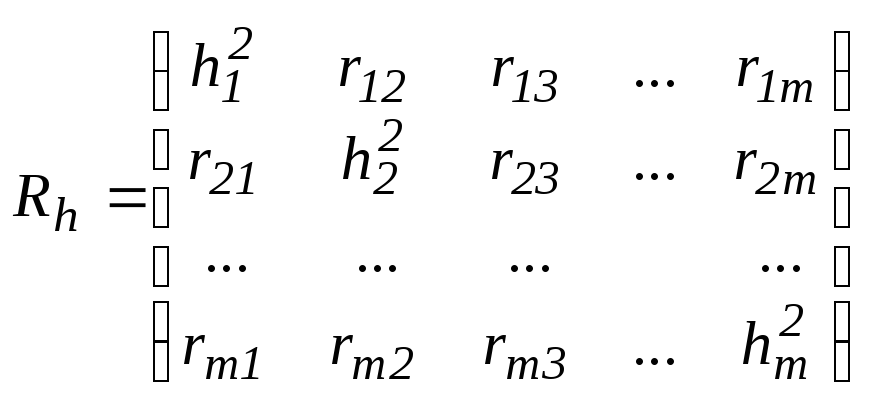
с h²_j<1, т.е. вариация признаков ()может быть объяснена не на 100 %, а несколько меньше, с учетом существования их нераскрываемой характерности.

Существуют достаточно простые методы поиска общностей h²_j:

• метод наибольшей корреляции – на главной диагонали с положительным знаком записывается наибольший по величине коэффициент корреляции;

• метод Барта – по каждому столбцу матрицы R вначале находят среднее значение коэффициентов корреляции , затем, если сравнительно велико, за общность принимается значение, которое несколько выше наибольшего в столбце коэффициента корреляции, и, если– сравнительно малое значение, общность будет несколько меньше наибольшего в столбце коэффициента корреляции;

• метод триад – общности для каждого j-го столбца R вычисляют по формуле , гдеr_ik и r_il – коэффициентыкорреляции, наибольшие в столбце;

метод малого центроида – для каждой переменной j строится корреляционная матрица размерности 4x4; включая саму переменную в эту матрицу, записывают оценки корреляции трех других переменных, особенно тесно связанных с первой; по данным малой матрицы корреляций и рассчитывают общности:

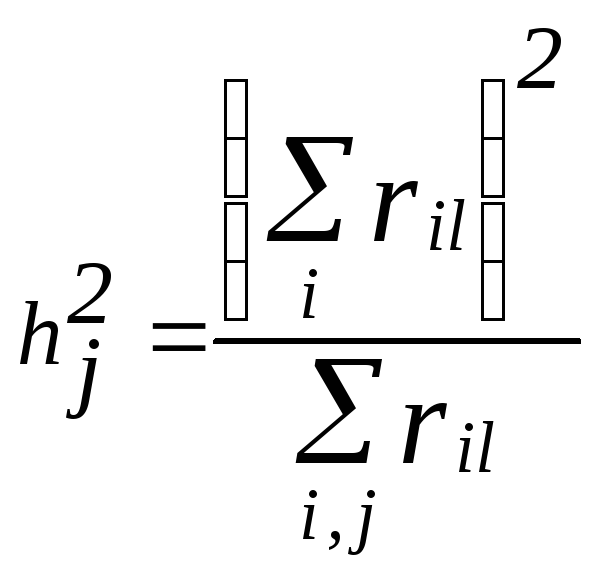, где– сумма элементов первого столбца;– сумма всех элементов матрицы 4×4.

На пятом шаге возникает проблема на этапе построения матрицы отображения А и заключается в выборе оптимального метода для поиска весовых коэффициентов a_ij элементов матрицы А. Напомним, что наилучшие решения обычно находят при помощи современных методов факторного анализа: главных факторов, максимального правдоподобия и др. В общем случае выделенные факторы не обязательно ортогональны (R = АСА'), и тогда векторы (столбцы) матрицы А будут линейно-зависимыми.

Выполнение шага 6 алгоритма и решение проблемы вращения пространства общих факторов необязательно. Потребность в этом возникает, когда пространственное расположение общих факторов F_r нелогично или трудно поддается интерпретации.

Возможность появления нелогичных первых результатов анализа объясняется неопределяемым четко и незадаваемым положением факторных осей в пространстве, отсутствием изначально какой-либо пространственной привязки для осей F_r.

На рис. 8.6 показаны два различных положения в пространстве факторных осей (F₁ и F₂). Легко заметить, что изменение положения F₁, F₂ одновременно приводит к изменению координат исходных признаков X_j. Цель поворота – преобразование координат (факторных нагрузок) таким образом, чтобы факторообразующие признаки имели наибольшие нагрузки, близкие к единице (|a_ir|1), а остальные признаки – минимальные значения, близкие к нулю, т.е. добиваются экономичного описания данных.

Рис. 8.6. Исходные признаки X_j в пространстве общих факторов F₁ и F₂

Повороты осей могут быть ортогональными и косоугольными (рис. 8.7). Предпочтительно, хотя и более трудно выполнимо и интерпретируемо, косоугольное вращение, при этом, как видно из рис. 8.7,б, значительно повышаются возможности оптимального отображения сгущений признаков в пространстве R^F.

На рис. 8.7,а ось F'₁ после поворота F, очевидно, займет более рациональное положение, но из-за жесткости осевой конструкции положение F’₂ удаляется от оптимального; на рис. 8.7,б косоугольным вращением (α ≠90°) приходят к оптимизации положения сразу обеих осей F'₁ и F'₂.

Рис. 8.7. Гипотетические результаты ортогонального (а) и косоугольного (б) вращений пространства общих факторов

Вращение пространства общих факторов F_r не изменяет величин общностей h²_j, и по-прежнему АА' = R⁺ или АСА' = R⁺ приR⁺ →R. На заключительном этапе алгоритма рассчитывают матрицу значений факторов F, ее элементы – это факторные значения f_ir для каждой единицы наблюдения. Тем самым определяем положение п объектов в пространстве R^F с r-числом факторных осей (рис. 8.8).

Р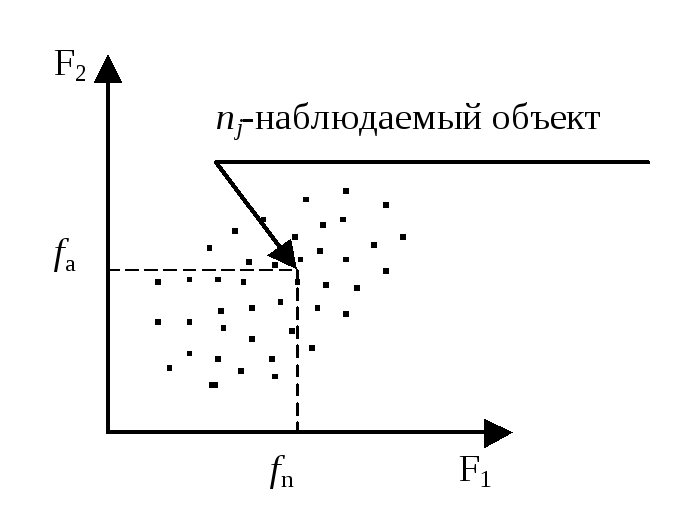ис. 8.8. Расположение объектов в пространстве двух факторных осей

Так как число общих факторов F_r, как правило, значительно меньше числа исходных признаков X_j, матрица F имеет размерность п  r в отличие от исходной матрицы X размерностью п  т. Проблема заключается в выборе методики перехода от матрицы исходных данных Z (или X) по известной матрице факторного отображения A к матрице F, ее решают обычно одним из двух методов: во первых, вращением пространства исходных признаков (R^z), а значит, посредством алгебраического произведения отображающих матриц Z(X) и А, т.е. F=f(Z, А), где f – функция линейной функциональной формы связи; во-вторых, F находят с помощьюмножественного регрессионного анализа: F = (В, Z, R, А) +£ (линейная стохастическая форма связи), где В – матрица коэффициентов регрессии размерностью r  m; ее элементы b_jr – регрессионные коэффициенты каждого из факторов F_r по переменной X_j.

Алгоритмы факторного анализа отличаются, как видим, трудоемкостью, их полное выполнение возможно при условии использования технических средств.