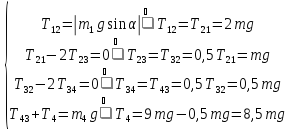- •Расчётно-графическая работа № 3 на тему: «Сложное движение точки»
- •Решение:
- •Получить то же самое дифференциальное уравнение движения системы, используя теорему об изменении кинетической энергии механической системы в дифференциальной форме.
- •Получить дифференциальное уравнение движения механической системы на основании общего уравнения динамики.
-
Получить то же самое дифференциальное уравнение движения системы, используя теорему об изменении кинетической энергии механической системы в дифференциальной форме.
На
систему действуют следующие внешние
силы: силы тяжести
 – катка 1,
– катка 1,
 – блока 2,
– блока 2,
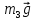 – блока 3 и
– блока 3 и
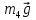 – цилиндра 4,
– цилиндра 4,
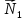 – нормальная реакция груза 1, сила
натяжения троса
– нормальная реакция груза 1, сила
натяжения троса
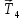 и вращающий момент
и вращающий момент
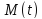 .
.
Применим
теорему об изменении кинетической
энергии механической системы в
дифференциальной форме:
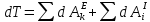 ,
где
,
где
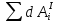 – сумма работ внутренних сил на
элементарном перемещении (для этой
системы, состоящей из абсолютно твердых
тел, соединенных нерастяжимыми нитями:
– сумма работ внутренних сил на
элементарном перемещении (для этой
системы, состоящей из абсолютно твердых
тел, соединенных нерастяжимыми нитями:
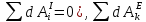 - сумма работ внешних сил на этом же
перемещении, то есть
- сумма работ внешних сил на этом же
перемещении, то есть
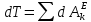 .
.
Кинетическая
энергия системы равна:
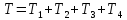 ,
где
,
где
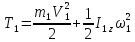 – кинетическая энергия катка 1, движущегося
плоско-параллельно;
– кинетическая энергия катка 1, движущегося
плоско-параллельно;
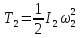 – кинетическая энергия цилиндра 2,
вращающегося вокруг неподвижной оси;
– кинетическая энергия цилиндра 2,
вращающегося вокруг неподвижной оси;
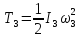 – кинетическая энергия цилиндра 3,
вращающегося вокруг неподвижной оси;
– кинетическая энергия цилиндра 3,
вращающегося вокруг неподвижной оси;
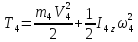 - кинетическая энергия цилиндра 4,
движущегося плоско-параллельно.
- кинетическая энергия цилиндра 4,
движущегося плоско-параллельно.
Таким
образом, получаем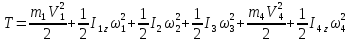 .
.
Выразим
скорости центров масс и угловые скорости
тел системы через линейную скорость
катка 1 (составим уравнения связей).
Мгновенный центр скоростей катка 1
находится в точке
 ,
а мгновенный центр скоростей цилиндра
4 – в точке
,
а мгновенный центр скоростей цилиндра
4 – в точке
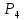 .
Находим
.
Находим
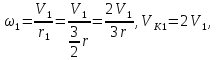
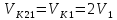 ,
но
,
но
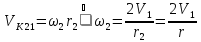
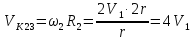 ,
,
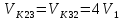 ,
,
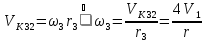
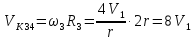
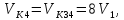 но
но
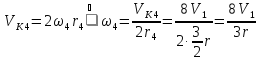 ,
,
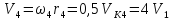 .
.
Учитывая исходные данные, имеем
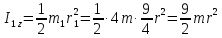 ,
,
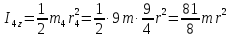 ,
,
Подставляя все в выражение для кинетической энергии, получаем:
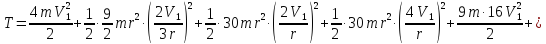

Найдем сумма элементарных работ внешних сил:
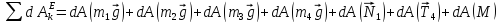 ,
,
где
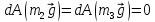 ,
так как точки приложения сил тяжести
цилиндров 2 и 3 – неподвижны;
,
так как точки приложения сил тяжести
цилиндров 2 и 3 – неподвижны;
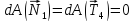 ,
так как эти силы приложены в мгновенных
центрах скоростей соответствующих тел;
,
так как эти силы приложены в мгновенных
центрах скоростей соответствующих тел;
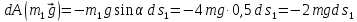 ;
;
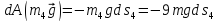
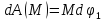
Так
как соотношения между перемещениями,
такие же как и между скоростями, то
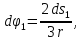
 .
.
В
результате получаем
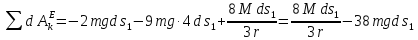 .
.
В итоге имеем следующее уравнение:

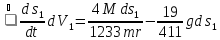
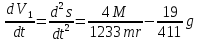 .
.
Получили дифференциальное уравнение второго порядка относительно S.
-
Получить дифференциальное уравнение движения механической системы на основании общего уравнения динамики.
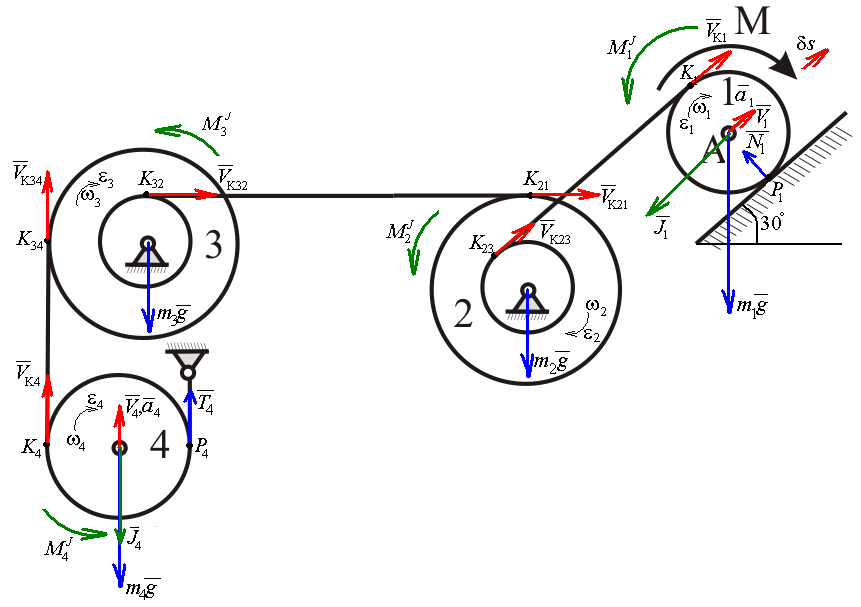
Так как система приходит в движение из состояния покоя, то направления ускорений тел соответствуют направлениям их движения.
Будем считать, что движение системы таково, что каток 1 поднимается.
Покажем
внешние силы: силы тяжести
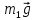 – катка 1,
– катка 1,
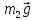 – блока 2,
– блока 2,
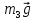 – блока 3 и
– блока 3 и
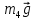 – цилиндра 4,
– цилиндра 4,
 – нормальная реакция груза 1, сила
натяжения троса
– нормальная реакция груза 1, сила
натяжения троса
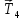 и вращающий момент
и вращающий момент
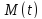 .
.
Приложим
силы инерции. Сила инерции катка 1,
совершающего плоско-параллельное
движение, приводятся к вектору
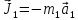 ,
где
,
где
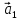 –
ускорение центра масс катка 1 (точка А),
и к паре сил, момент которой
–
ускорение центра масс катка 1 (точка А),
и к паре сил, момент которой
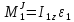 ,
где
,
где
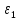 – угловое ускорение катка 1.
– угловое ускорение катка 1.
Силы
инерции цилиндра 2, вращающегося вокруг
неподвижной оси с угловым ускорением
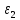 ,
приводятся к паре, момент которой
,
приводятся к паре, момент которой
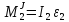 .
.
Силы
инерции цилиндра 3, вращающегося вокруг
неподвижной оси с угловым ускорением
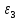 ,
приводятся к паре, момент которой
,
приводятся к паре, момент которой
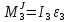 .
.
Сила
инерции цилиндра 4, совершающего
плоско-параллельное движение, приводятся
к вектору
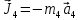 ,
где
,
где
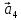 –
ускорение центра масс цилиндра 4 (точка
В), и к паре сил, момент которой
–
ускорение центра масс цилиндра 4 (точка
В), и к паре сил, момент которой
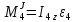 ,
где
,
где
 – угловое ускорение цилиндра 4.
– угловое ускорение цилиндра 4.
Сообщим системе возможное перемещение в направлении ее действительного движения.
Составим общее уравнение динамики:
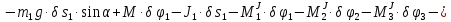
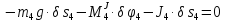
где
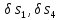 – линейные перемещения центров тяжести
цилиндров 1 и 4,
– линейные перемещения центров тяжести
цилиндров 1 и 4,
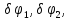
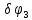 и
и
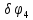 – углы поворотов цилиндров 1, 2, 3, 4.
– углы поворотов цилиндров 1, 2, 3, 4.
Зависимости между возможными перемещениями такие же, как и между соответствующими скоростями. Поэтому выразим скорости центров масс и угловые скорости тел системы через линейную скорость катка 1 (составим уравнения связей).
Мгновенный
центр скоростей катка 1 находится в
точке
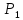 ,
а мгновенный центр скоростей цилиндра
4 – в точке
,
а мгновенный центр скоростей цилиндра
4 – в точке
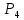 .
.
Находим
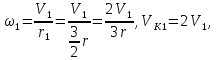
 ,
но
,
но
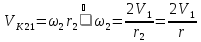
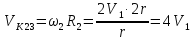 ,
,
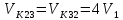 ,
,

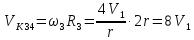
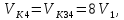 но
но
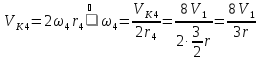 ,
,
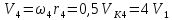 .
.
Такие же зависимости и между возможными перемещениями

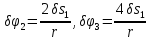 ,
,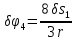 ,
,

и
между ускорениями
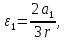
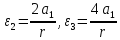 ,
,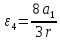 ,
,
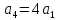 .
.
Таким образом, общее уравнение динамики принимает вид:
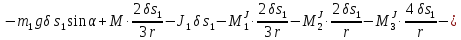
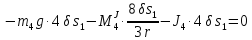
Учитывая исходные данные, имеем
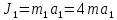 ,
,
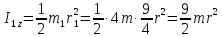 ,
,
 ,
,
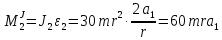 ,
,
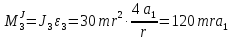 ,
,
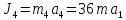 ,
,
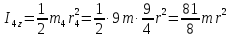 ,
,
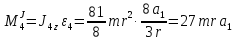
В результате общее уравнение динамики приобретает следующий вид:
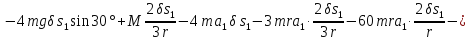
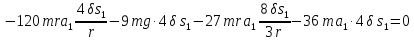
или
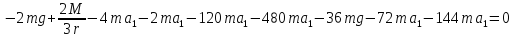
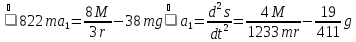
Получили дифференциальное уравнение второго порядка относительно s.
-
Получить то же самое дифференциальное уравнение движения системы, составив для неё уравнения Лагранжа 2-го рода.
Данная
механическая система имеет одну степень
свободы, поэтому в качестве обобщенной
координаты выберем перемещение центра
масс катка 1, то есть
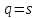 ,
тогда
,
тогда
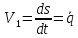 .
Уравнение Лагранжа 2 рода имеет вид:
.
Уравнение Лагранжа 2 рода имеет вид:
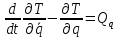 ,
где
,
где
 – кинетическая энергия системы,
– кинетическая энергия системы,
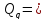
 – обобщенная сила.
– обобщенная сила.
Таким
образом, получаем
 ,
,
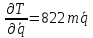 ,
,

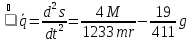
Получили дифференциальное уравнение второго порядка относительно s.
-
Убедившись в совпадении результатов, полученных четырьмя независимыми способами, проинтегрировать дифференциальное уравнение движения системы, получив зависимость
 координаты точки
координаты точки
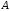 от времени.
от времени.
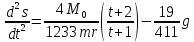
 .
.
Так
как система начинает двигаться из
состояния покоя, то при


То есть


Так
как при
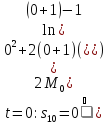
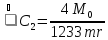 .
.
Таким
образом, получили следующую зависимость
координаты точки
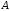 от времени
от времени
-
Построить графики зависимостей
 и
и
 .
.
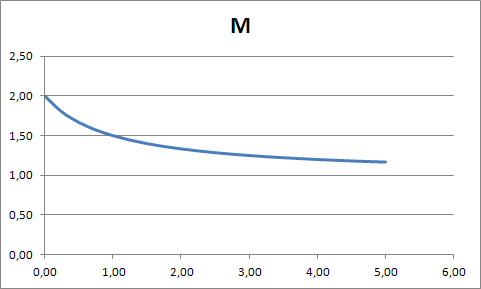
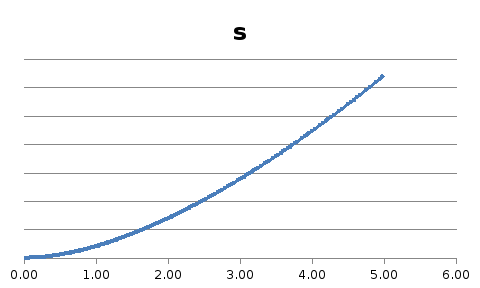
Построим
график зависимости
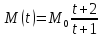 :
:
Построим
график зависимости
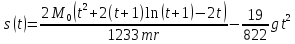 .
.
Данный
график будет разным в зависимости от
отношения
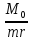 .
.
Если
 ,
то график имеет вид
,
то график имеет вид
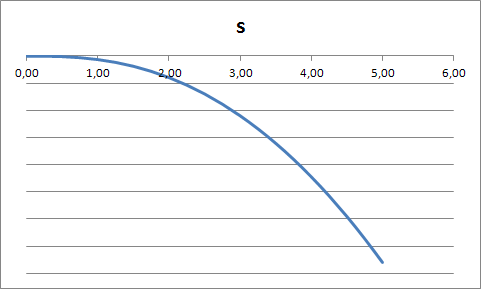
Если
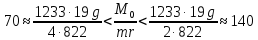 ,
то график имеет вид
,
то график имеет вид
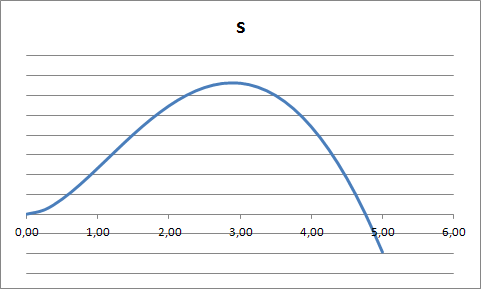
Причем
чем ближе отношение
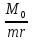 к 70, тем ближе вершина параболы к оси y
и
оси х,
и
тем больше график напоминаете предыдущий,
а чем ближе отношение
к 70, тем ближе вершина параболы к оси y
и
оси х,
и
тем больше график напоминаете предыдущий,
а чем ближе отношение
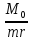 к 140, тем больше график напоминает тот,
что расположен ниже.
к 140, тем больше график напоминает тот,
что расположен ниже.
Если
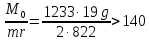 ,
то график имеет вид
,
то график имеет вид
-
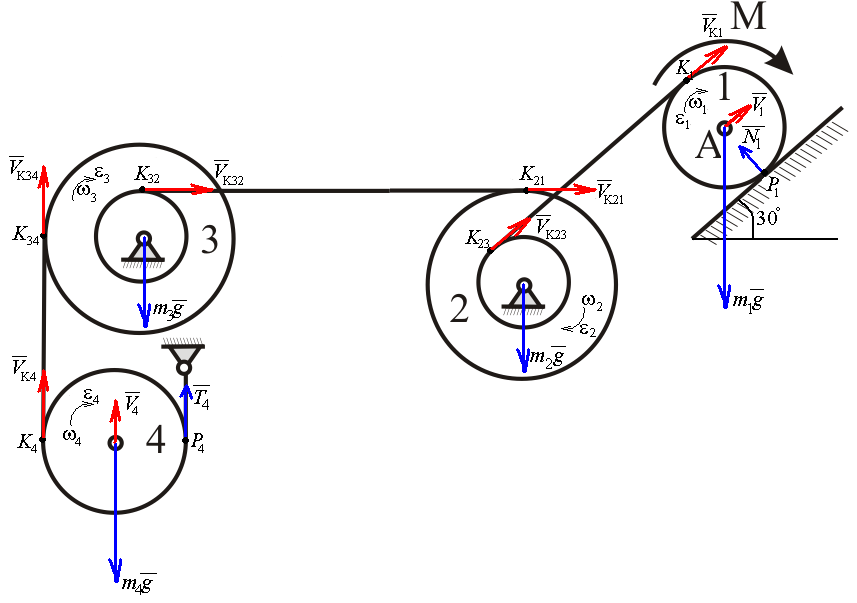
Определить натяжения тросов в начальный момент времени (при
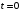 ).
).
При
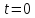 натяжения тросов найдем по формулам:
натяжения тросов найдем по формулам: