
- •Расчётно-графическая работа № 3 на тему: «Сложное движение точки»
- •Решение:
- •Получить то же самое дифференциальное уравнение движения системы, используя теорему об изменении кинетической энергии механической системы в дифференциальной форме.
- •Получить дифференциальное уравнение движения механической системы на основании общего уравнения динамики.
Расчётно-графическая работа № 1 на тему:
«Кинематическое исследование движения точки»
Исходные данные:

 c.
c.
Решение:
-
По заданным уравнениям движения точки определить траекторию и изобразить её на чертеже.
Для определения траектории точки выразим
 и
и
 ,
после чего возведем выражения в квадрат
и затем их сложим:
,
после чего возведем выражения в квадрат
и затем их сложим:
 ,
,


Таким образом, получили, что траектория
точки – это эллипс с центром в точке
 и полуосями
и полуосями
 м,
м,
 м.
м.

-
Определить проекции вектора скорости на координатные оси и модуль вектора скорости.
 ;
;





 .
.
-
Определить проекции вектора ускорения на координатные оси и модуль вектора ускорения.





-
Вычислить и изобразить на чертеже начальное положение точки, вектор начальной скорости и вектор начального ускорения.
Найдем начальное положение точки в
момент времени
 c:
c:
 рад;
рад;
 м;
м;
 м;
м;
Проекции и модуль вектора скорости в
начальный момент времени
 c:
c:

 м/с;
м/с;
 м/с;
м/с;
 м/с.
м/с.
Проекции и модуль вектора ускорения в
начальный момент времени
 c:
c:

 м/с2
м/с2

 м/с2;
м/с2;
 м/с2.
м/с2.

-
Выбрать начало и направление отсчёта дуговой координаты и получить закон изменения дуговой координаты со временем.
В качестве начала отсчёта дуговой
координаты возьмем точку
 ,
направление отсчёта – против хода
часовой стрелки.
,
направление отсчёта – против хода
часовой стрелки.

Изменение дуговой координаты по времени
можно найти следующим образом:
 .
.
Так как начало отчета мы совместили с
точкой
 ,
то при
,
то при
 c:
c:
 .
.
Таким образом,
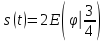 или
или
 ,
где
,
где
 .
.
-
Вычислить касательное и нормальное ускорения точки.
Касательное ускорение точки:



Нормальное ускорение точки:

где
 - радиус кривизны траектории движения
точки выводится из уравнения эллипса
- радиус кривизны траектории движения
точки выводится из уравнения эллипса
 ,
,
 .
.
-
Построить графики зависимости от времени дуговой координаты, проекции вектора скорости на касательную, касательного ускорения и пройденного пути.
График зависимости от времени дуговой координаты
 :
:

График зависимости от времени проекции
вектора скорости на касательную
 :
:

График зависимости от времени касательного
ускорения
 :
:

График зависимости от времени пройденного пути

-
Для заданного момента времени
 определить декартовы и дуговую координаты
точки, вектор скорости, вектор ускорения
и все его проекции. Полученные результаты
изобразить на чертеже.
определить декартовы и дуговую координаты
точки, вектор скорости, вектор ускорения
и все его проекции. Полученные результаты
изобразить на чертеже.
Найдем положение точки в заданный момент
времени
 c:
c:
 рад;
рад;
 м;
м;
 м;
м;
 м.
м.
Проекции и модуль вектора скорости в
заданный момент времени
 c:
c:

 м/с;
м/с;
 м/с;
м/с;
 м/с.
м/с.
Найдем направляющий косинус вектора
скорости
 (угол, который образует вектор скорости
(угол, который образует вектор скорости
 с положительным направлением оси х)
с положительным направлением оси х)

Проекции и модуль вектора ускорения в
заданный момент времени
 c:
c:

 м/с2
м/с2

 м/с2;
м/с2;
 м/с2.
м/с2.
Найдем направляющий косинус вектора
ускорения
 (угол, который образует вектор ускорения
(угол, который образует вектор ускорения
 с положительным направлением оси х):
с положительным направлением оси х):
 .
.
Касательное и нормальное ускорения в
заданный момент времени
 c:
c:
 м/с2;
м/с2;
 м
м
 м/с2.
м/с2.

Расчётно-графическая работа № 3 на тему: «Сложное движение точки»
По ободу диска
радиуса
 движется
точка
движется
точка
 .
Уравнение движения задано в таблице;
там же указано начало отсчёта
.
Уравнение движения задано в таблице;
там же указано начало отсчёта
 дуговой координаты
дуговой координаты
 .
Положительное направление отсчёта –
по ходу часовой стрелки, если смотреть
навстречу оси
.
Положительное направление отсчёта –
по ходу часовой стрелки, если смотреть
навстречу оси
 .
Уравнение вращения диска задано в
таблице. Положительным направлением
вращения считается направление против
хода часовой стрелки, если смотреть с
положительного конца
.
Уравнение вращения диска задано в
таблице. Положительным направлением
вращения считается направление против
хода часовой стрелки, если смотреть с
положительного конца
 оси вращения
оси вращения
 .
Для момента времени
.
Для момента времени
 с
определить абсолютную скорость и
абсолютное ускорение точки
с
определить абсолютную скорость и
абсолютное ускорение точки
 .
.
Исходные данные:
 ,
,
 ,
,
 c.
c.

Найти: абсолютную
скорость
 и абсолютное ускорение
и абсолютное ускорение
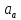 точки М
для момента времени
точки М
для момента времени
 c.
c.
Решение:
Будем считать, что
в заданный момент времени плоскость
чертежа совпадает с плоскостью диска.
Положение точки М
на диске определяется расстоянием
 .
.
При
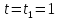 с:
с:
 . Найдем угол, на который повернулся
радиус при движении точки М
по окружности:
. Найдем угол, на который повернулся
радиус при движении точки М
по окружности:
 рад.
рад.

Абсолютную скорость
точки М
найдем как геометрическую сумму
относительной и переносной скоростей:
 .
.
Модуль относительной
скорости
 ,
где
,
где

При
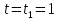 с:
с:
 ;
;
 .
.
Положительный
знак у
 показывает, что вектор
показывает, что вектор
 направлен в сторону положительных
значений
направлен в сторону положительных
значений
 ,
перпендикулярно радиусу окружности,
то есть вертикально вниз.
,
перпендикулярно радиусу окружности,
то есть вертикально вниз.
Модуль переносной
скорости
 ,
где
,
где
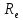 – радиус окружности, описываемой той
точкой тела, с которой в данный момент
совпадает точка М,
– радиус окружности, описываемой той
точкой тела, с которой в данный момент
совпадает точка М,
 ;
;
 - модуль угловой скорости тела:
- модуль угловой скорости тела:
 .
.
При
 с:
с:
 ;
;
 .
.
Положительный
знак у величины
 показывает, что вращение диска происходит
вокруг оси
показывает, что вращение диска происходит
вокруг оси
 в сторону отсчета угла
в сторону отсчета угла
 .
Поэтому вектор
.
Поэтому вектор
 направлен по оси
направлен по оси
 ,
перпендикулярно плоскости рисунка на
нас (параллельно оси z).
,
перпендикулярно плоскости рисунка на
нас (параллельно оси z).
Таким образом,
модуль переносной скорости при
 с равен
с равен
 .
.
Вектор
 направлен перпендикулярно радиусу
направлен перпендикулярно радиусу
 в
сторону вращения.
в
сторону вращения.
Модуль абсолютной скорости точки М находим способом проекций:


 или
или
 .
.

Абсолютное
ускорение точки равно геометрической
сумме относительного, переносного и
кориолисова ускорений:
 ,
или в развернутом виде
,
или в развернутом виде
 .
.
Модуль относительного
касательного ускорения
 ,
где
,
где

 .
.
При
 с:
с:
 ;
;
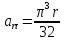 .
.
Отрицательный
знак
 показывает, что вектор
показывает, что вектор
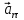 направлен в сторону отрицательных
значений
направлен в сторону отрицательных
значений
 ,
перпендикулярно радиусу окружности,
то есть вертикально вверх. Знаки
,
перпендикулярно радиусу окружности,
то есть вертикально вверх. Знаки
 и
и
 не одинаковы; следовательно, относительное
движение точки М
замедленное.
не одинаковы; следовательно, относительное
движение точки М
замедленное.
Относительное
нормальное ускорение
 ,
то есть при
,
то есть при
 с:
с:
 .
.
Вектор
 направлен к центру диска, то есть
горизонтально влево.
направлен к центру диска, то есть
горизонтально влево.
Модуль
переносного вращательного ускорения
 ,
где
,
где
 – модуль углового ускорения диска:
– модуль углового ускорения диска:
 .
.
При
 с:
с:
 ;
;
 .
.
Таким образом,
получаем
 .
.
Модуль переносного
центростремительного ускорения
 или
или
 .
.
Вектор
 направлен к центру вращения
направлен к центру вращения
 .
.
Кориолисово
ускорение
 .
Модуль кориолисова ускорения
.
Модуль кориолисова ускорения
 ,
где
,
где
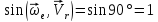 .
.
С учетом найденных
выше значений
 и
и
 получаем при
получаем при
 с:
с:
 .
.
Вектор
 направлен согласно правилу векторного
произведения, то есть перпендикулярно
одновременно векторам
направлен согласно правилу векторного
произведения, то есть перпендикулярно
одновременно векторам
 ,
в ту сторону, откуда поворот от
,
в ту сторону, откуда поворот от
 к
к
 виден против хода часовой стрелки, то
есть вдоль оси x
вправо.
виден против хода часовой стрелки, то
есть вдоль оси x
вправо.
Модуль абсолютного ускорения точки М находим способом проекций:
 ;
;
 ;
;
 ;
;

 .
.

Ответ:
 ,
,
 .
.
Расчётно-графическая работа на тему:
«Динамическое исследование движения механической системы»
Механическая
система состоит из четырёх цилиндров,
связанных между собой нерастяжимыми
тросами. Каток 1 массы
 радиуса
радиуса
 катится без скольжения по неподвижной
плоскости, наклонённой под углом
катится без скольжения по неподвижной
плоскости, наклонённой под углом
 к горизонту. Блоки 2 и 3 – одинаковые
сплошные однородные сдвоенные цилиндры
массы
к горизонту. Блоки 2 и 3 – одинаковые
сплошные однородные сдвоенные цилиндры
массы
 с внутренним радиусом
с внутренним радиусом
 и наружным радиусом
и наружным радиусом
 .
Даны моменты инерции цилиндров:
.
Даны моменты инерции цилиндров:
Система
приводится в движение из состояния
покоя моментом
 ,
приложенным к катку 1.
,
приложенным к катку 1.

Исходные
данные:

При выполнении задания необходимо:
-
Используя общие теоремы динамики, составить систему уравнений, описывающих движение заданной механической системы. Исключая из этой системы уравнений внутренние силы, получить дифференциальное уравнение, служащее для определения зависимости
 координаты точки
координаты точки
 от времени – дифференциальное уравнение
движения системы.
от времени – дифференциальное уравнение
движения системы.
Рассмотрим
каток 1 и составим для него два уравнения,
воспользовавшись двумя теоремами –
теоремой о движении центра масс в
проекции на ось


и
теоремой об изменении кинетического
момента:
 , где
, где
 ,
,
 ,
то есть второе уравнение имеет вид
,
то есть второе уравнение имеет вид
 .
.
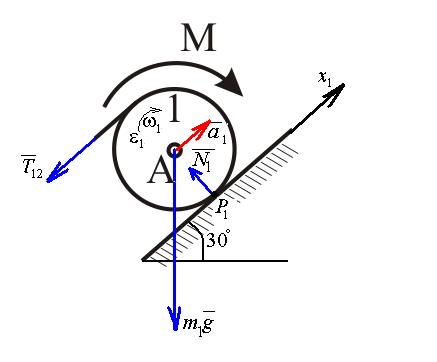
Рассмотрим
цилиндр 2 и составим для него одно
уравнение, используя теорему об изменении
кинетического момента:
 ,
где
,
где
 ,
то есть
,
то есть
 .
.
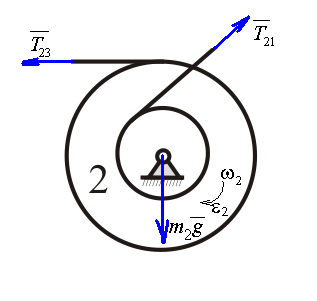
Рассмотрим
цилиндр 3 и составим для него одно
уравнение, используя теорему об изменении
кинетического момента –
 ,
где
,
где
 ,
то есть
,
то есть
 .
.

Рассмотрим
цилиндр 4 и составим для него два
уравнения, воспользовавшись двумя
теоремами – теоремой о движении центра
масс в проекции на ось


и
теоремой об изменении кинетического
момента:
 , где
, где
 ,
,
 ,
то есть второе уравнение имеет вид
,
то есть второе уравнение имеет вид
 .
.

Таким образом, получили систему из 6 уравнений:

Исключим
из этой системы уравнений внутренние
силы и выразим все кинетические
характеристики через ускорение центра
масс катка 1 -
 ,
воспользовавшись равенствами:
,
воспользовавшись равенствами:

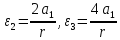 ,
, ,
,
 (подробнее о кинематических зависимостях
написано в п.2 и п.3). При выводе уравнения
использовали, что
(подробнее о кинематических зависимостях
написано в п.2 и п.3). При выводе уравнения
использовали, что
 ,
,
 ,
,
 .
В каждом уравнении выразили силы
натяжения, а затем все уравнения сложили,
в
результате получили
.
В каждом уравнении выразили силы
натяжения, а затем все уравнения сложили,
в
результате получили
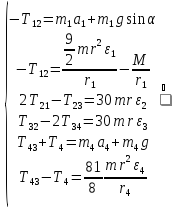


 .
.
Получили дифференциальное уравнение второго порядка относительно S.
