83. Степенные ряды. Ряд Тейлора, ряд Маклорена.

Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

в котором коэффициенты an берутся из некоторого кольца R.

Степенной ряд от n переменных — это формальное алгебраическое выражение вида:

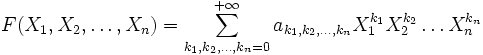
или, в мультииндексных обозначениях,

где X — это вектор , α — мультииндекс , Xα — одночлен . Пространство степенных рядов от n переменных и коэффициентами из R обозначается . В нём определены операции сложения, умножения, дифференцирования по каждой переменной и n-местной суперпозиции.

Сходимость степенных рядов

Из формального степенного ряда с вещественными или комплексными коэффициентами путем приписывания формальной переменной X какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).

Ряд Тейлора Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд называется рядом Тейлора функции f в точке a.

В случае, если a = 0, этот ряд также называется рядом Макло́рена.

Свойства

• Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.

• Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например, Коши предложил такой пример:

(ХЗ нужна ли?)Теорема

Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, U(a,ε)

Пусть

Пусть p — произвольное положительное число,

тогда: точка при x < a или при x > a:

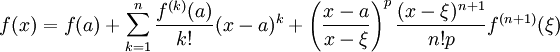
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

85. Классическое определение вероятности. Статистическое понятие вероятности. Геометрический подход к вероятности. Аксиоматическое построение теории вероятностей. Свойства вероятностей.

Классическое определение вероятности.

Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.

Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:

Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.

Статистическое понятие вероятности (частота события)

Частота события x — отношение N(x) / N числа N(x) наступлений этого события в N испытаниях к числу испытаний N.

Очевидно, что 0<=N(x)/N <=1. В случайном эксперименте с равновероятными исходами, в котором из соображений симметрии принимается «классическое определение вероятности», частота N(x) / N события x совпадает с его вероятностью P(x). В общей ситуации, если испытания независимы и априори постулируется существование вероятности P(x) события x, то при любом сколь угодно малом числе e>0 и больших N практически достоверно, что частота N(x) / N удовлетворяет неравенству |N(x)/N – P(x)| <= e

Такая статистическая близость частоты события к его вероятности позволяет в математической статистике при решении задачи оценивания неизвестной вероятности по результатам наблюдений принимать частоту в качестве приближенного значения вероятности, или статистической оценки вероятности.

Геометрический подход к вероятности

Т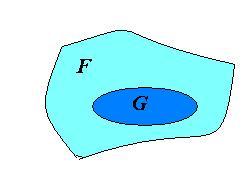очку наудачу бросают в фигуруF на плоскости. Какова вероятность того, что точка попадает в некоторую фигуру G, которая содержится в фигуре F.

Ответ зависит от того, какой смысл мы вкладываем в выражение «бросить точку наудачу».

Обычно это выражение трактуют так:

1. Брошенная точка может попасть в любую часть фигуры F.

2. Вероятность того, что точка попадает в некоторую фигуру G внутри фигуры F, прямо пропорциональна площади фигуры G.

Подведем итог: пусть и- площади фигурF и G . Вероятность события А «точка Х принадлежит фигуре G, которая содержится в фигуре F», равна

.

Заметим, что площадь фигуры G не больше, чем площадь фигуры F, поэтому

Аксиоматическое построение теории вероятностей

Пусть Ω — множество элементов ω, которые называются элементарными событиями, а F — множество подмножеств Ω, называемых случайными событиями (или просто — событиями), а Ω — пространством элементарных событий.

Аксиома I (алгебра событий): F является алгеброй событий.

Аксиома II (существование вероятности событий): Каждому событию x из F поставлено в соответствие неотрицательное действительное число P(x), которое называется вероятностью события x.

Аксиома III (нормировка вероятности): P(Ω) = 1.

Аксиома IV (аддитивность вероятности): Если события x и y не пересекаются, то P(x+y)=P(x)+P(y)

Совокупность объектов (Ω, F, P), удовлетворяющая аксиомам I—IV, называется вероятностным пространством (у Колмогорова: поле вероятностей).

Свойства вероятностей

Нормировка вероятности: 0 ≤ p (A) ≤ 1 для любого события A

Вероятность противоположного события: p(A)+p(­­­­­­­­–A)=1

Для независимых событий A и B: p (A и B) = p(A)*p(B)

p (A или B) = p(A) + p (B)

Условная вероятность: p(AB) = p (B) * p (A|B)

Формула полной вероятности:

p (B) = p (B | A1) p (A1) + p (B | A2) p (A2) + p (B | A3) p (A3) +… + p (B | Ak) p (Ak)