80. Производная функции, ее геометрический смысл. Правила дифференцирования.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Определение производной функции через предел:

Пусть в некоторой окрестности точки определена функция Производной функции f в точке x0 называется предел, если он существует,

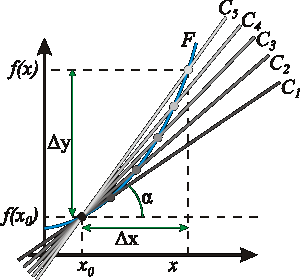
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0.

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

C' = 0

x' = 1

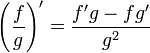
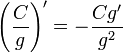
81. Определение и свойства неопределенного интеграла.

Неопределённый интегра́л для функции - это совокупность всех первообразных данной функции.

Если функция определена и непрерывна на промежутке и — ее первообразная, то есть при , то

, где С — произвольная постоянная.

Свойства неопределённого интеграла

Если , то и , где - произвольная функция, имеющая непрерывную производную

81. Определнный интеграл, его геометрический смысл, свойства.

Определённый интеграл — аддитивный монотонный нормированный функционал(???!!!), заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x0 < x1 < x2 < xn = b Тогда говорят, что произведено разбиение RR отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм ΘR при , если он существует независимо от разбиения R и выбора точек ξi, т.е. 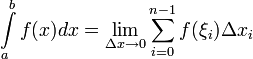(1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

a – нижний предел. b – верхний предел. f(x) – подынтегральная функция. λR - длина частичного отрезка. σR – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R. λR - максимальная длина част. отрезка.

Геометрический смысл

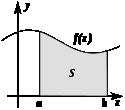Определённый интеграл как площадь фигуры

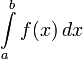Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

СВОЙСТВА(????) наверное такие же как и у неопределенного с небольшой поправкой на [a,b]