Вопрос №8

Вопрос №8.

Расчёт координат места судна аналитическим способом при избыточном числе линий положения. Метод наименьших квадратов, ковариационные матрицы погрешностей измерений и погрешностей координат, понятие геометрического фактора. Априорная и апостериорная оценка точности обсервации.

Основные сведения о методе наименьших квадратов

Число навигационных измерений, используемых для опреде­ления места судна, очень существенно. Если измеряются два навигационных параметра и решается задача определения ∆φ и ∆λ, то говорят, что в задаче отсутствует избыточность, т. е. система линейных уравнений линий положения совместна и практически всегда имеет решение. Исключение составляют па­раллельные линии положения.

С математической точки зрения гарантия решения системы уравнений, несомненно, является положительным качеством, но хорошо ли это с позиций навигации? Конечно, нет. Отсутствие избыточности измерений приводит к неконтролируемости влия­ния различных видов погрешностей на результат, и особенно опасны грубые промахи и систематические погрешности. По­этому в этих целях, а также для повышения точности обсерва­ции используют избыточное число измерений. Так, в случае оценки приращений координат ∆φ и ∆λ на плоскости минималь­но могут быть измерены три навигационных параметра, т. е. n = 3. В этой ситуации избыточность равна единице. Система уравнений линий положения будет иметь вид:

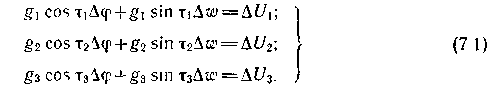
В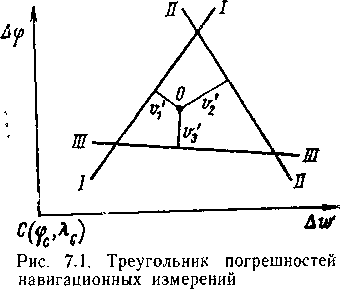озможно ли традиционное решение такой системы? Из-за наличия погрешностей измерений линии положения образуют фигуру погрешностей — треугольник (рис. 7.1), поэтому реше­ние любых двух уравнений из трех даст нам положение вер­шин этого треугольника погрешностей относительно начала ко­ординат. Это означает, что решение любой пары уравнений не обращает в тождество оставшееся уравнение. Такая система несовместна, т. е. решение любой пары несовместно с третьим уравнением. Какова же польза от такой избыточности, если уже на начальном этапе возникают трудности в поиске решения? Анализ размеров фигуры погрешностей и ее поведение в последовательности измерении дают полезные сведения о качестве измерительной на­вигационной информации.

Для того чтобы все же по­лучить согласованное реше­ние, необходимо ввести до­полнительные условия, ко­торые можно получить, если более детально представить систему (7.1). Другими сло­вами, в окрестности фигуры погрешностей необходимо выбрать точку (предпола­гаемое решение), относительно которой и можно было бы сфор­мулировать дополнительное условие.

Рис. 7.1 дает представление о фигуре погрешностей при n = 3. Здесь отрезки v'1, v'2, v'3 называются невязками. В спе­циальной литературе также встречается термин поправка или ошибка линии положения в зависимости от знака. Собственно в такой ситуации именно невязки и определяют решение отно­сительно фигуры погрешностей. Множество возможных сочета­ний невязок определяет множество решений, и задача заклю­чается в подборе наиболее простого и физически интерпрети­руемого условия. Если обозначить ∆Ui=Uo — Uc=—Li, то с учетом невязок систему (7.1) можно записать так:

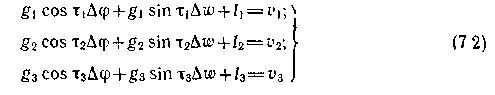
Здесь величины v1, v2, v3 — невязки, выраженные в единицах измерений, что более удобно для дальнейших выкладок. Для согласования системы (7.2) с рис. 7.1 необходимо выразить не­вязки v1 в линейных единицах, т. е. разделить все члены на мо­дули соответствующих градиентов:

Теперь становится очевидным, что избыточная система (7.1) превратилась в системы (7.2) — (7.2а) с недостаточным числом уравнений, так как невязки также неизвестны. Формально наи­более простое решение такой системы можно получить, если принять следующее условие:

Если невязки выражены в линейных единицах, то условие (7.3) запишется таким образом:

При увеличении числа измерений (n>3) возникает более сложная фигура погрешностей с числом вершин C²n = n(n—l)/2, но условие (7.3) дает однозначное решение системы уравнений линий положения при любом значении n. Его суть сводится к поиску «центра тяжести» фигуры погрешностей измерений, т. е. к определению некоторого среднего значения координат из мно­жества координат вершин фигуры.

Для того чтобы почувствовать это среднее, сконструируем из трех линий положения следующую фигуру погрешностей. Пусть две линии положения из трех параллельны (рис. 7.2). Эта конфигурация противоречит хорошей морской практике, но зато удобна для анализа. В такой ситуации естественно счи­тать, что место судна находится где-то на третьей линии поло­жения. Воспользуемся критерием, рассчитанным по формуле (7.3а). В результате получим, что минимуму критерия S соот­ветствует середина отрезка линии положения ///, заключенно­го между прямыми / и //. Решение системы уравнений называ­ется оптимальным в смысле выполнения условия S = min, т. е. при выполнении критерия минимума суммы квадратов невязок. Избыточность позволяет нам получить информацию о некото­рых средних значениях координат, а поэтому важным является утверждение, что оптимальная точка будет всегда находиться внутри фигуры погрешностей, если систематические погрешности δj = 0. Метод наименьших квадратов является наиболее универсальным средством обработки избыточной навигационной инфор­мации. Его основы бы­ли разработаны Лежандром и Гауссом в период с 1795 по 1805 г.

Р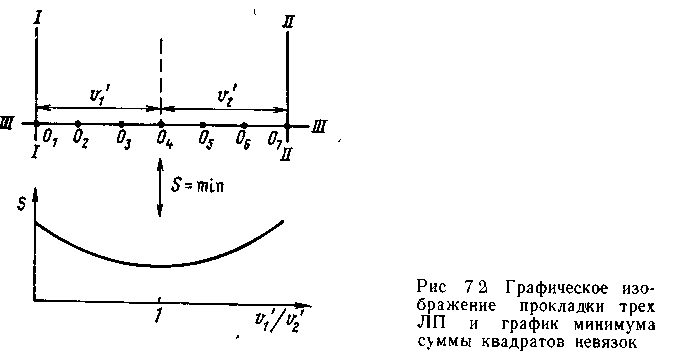азличные модифи­кации метода исполь­зуются в настоящее время для решения многих навигационных задач: -комплексирование навигационной информации -вычисление коэффициентов девиации и радиодевиации -определение коэффициентов дрейфа, точности счисления и т. п.

Для более удобного изложения дальнейшего материала вос­пользуемся методами линейной алгебры, что позволит сокра­тить и унифицировать записи. Обозначим матрицей А таблицу коэффициентов при неизвестных в системе (7.2), не ограничи­ваясь размерностью n.

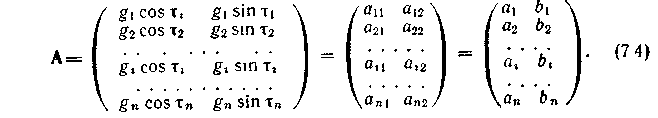
Введем следующие матрицы:

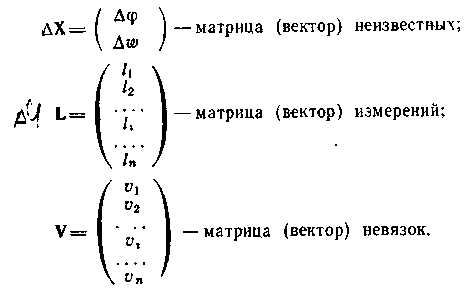
Теперь система (7.2) запишется более компактно:

Запишем в развернутой форме формулу (7.5), выполнив ум­ножение А на ∆Х, и получим знакомую систему (7.2). Размер­ности векторов ∆Х и L, т. е. величины k и n, формально не име­ют значения, и совершенно аналогичная по своей структуре ли­нейная система может быть составлена, если в вектор ∆Х, на пример, включить систематическую погрешность измерения на­вигационного параметра:

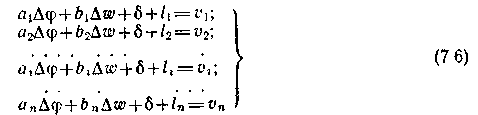
Здесь предполагается, что систематическая погрешность оди­накова для всех n измерений.

Для системы (7.6) матрицы А и ∆Х из системы (7.5) запи­шем так:

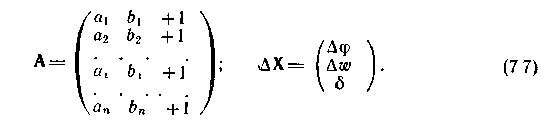
Для удобства записи в плоской задаче примем следующие обозначения: х = ∆φ и y = ∆ω