
- •Сходимость степенного ряда. Интервал сходимости, радиус сходимости и область сходимости
- •Исследование степенного ряда на сходимость
- •1) Подставляем значение в наш степенной ряд :
- •2) Исследуем второй конец интервала сходимости. При
- •1) Если , то получается следующий числовой ряд:
- •2) Что происходит на другом конце интервала? При – сходится.
2) Что происходит на другом конце интервала? При – сходится.
А вот и вознаграждение за мучения в предыдущем пункте! Получился точно такой же числовой ряд, сходимость которого мы только что доказали.
Ответ: область
сходимости исследуемого степенного
ряда: ![]()
Чуть менее сложный пример для самостоятельного решения:
Пример 9
Найти
область сходимости ряда ![]()
Достаточно для начала =)
В
заключение остановлюсь на одном моменте.
Во всех примерах мы использовали признак
Даламбера и составляли предел 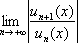 .
Всегда ли при решении заданий такого
типа нужно применять признак Даламбера?
Почти всегда. Однако в редких случаях
невероятно выгодно использовать
радикальный признак Коши и составлять
предел
.
Всегда ли при решении заданий такого
типа нужно применять признак Даламбера?
Почти всегда. Однако в редких случаях
невероятно выгодно использовать
радикальный признак Коши и составлять
предел ![]() ,
при этом техника и алгоритм решения
задачи остаются точно такими же! Что
это за случаи? Это те случаи, когда из
общего члена степенного ряда «хорошо»
(полностью) извлекается корень «энной»
степени.
,
при этом техника и алгоритм решения
задачи остаются точно такими же! Что
это за случаи? Это те случаи, когда из
общего члена степенного ряда «хорошо»
(полностью) извлекается корень «энной»
степени.
Следующий урок по теме – Разложение функций в степенные ряды. Примеры решений.
Желаю успехов!
Решения и ответы:
Пример
3: Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера:
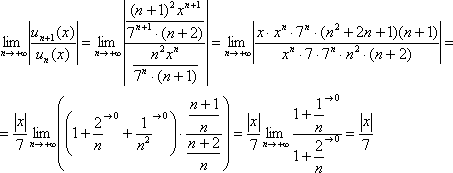 Ряд
сходится при
Ряд
сходится при ![]() Слева
нужно оставить только модуль, поэтому
умножаем обе части неравенства на
7
Слева
нужно оставить только модуль, поэтому
умножаем обе части неравенства на
7
![]()
![]() –
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала.
1)
При
–
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала.
1)
При ![]() Используем
признак Лейбница.
–
Ряд является знакочередующимся.
Используем
признак Лейбница.
–
Ряд является знакочередующимся.
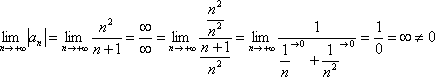 –
члены ряда не убывают по модулю.
Вывод:
Ряд расходится
2)
При
–
члены ряда не убывают по модулю.
Вывод:
Ряд расходится
2)
При ![]() Ряд
расходится, так как не выполнен необходимый
признак сходимости ряда.
Ответ:
Ряд
расходится, так как не выполнен необходимый
признак сходимости ряда.
Ответ: ![]() –
область сходимости исследуемого
степенного ряда
–
область сходимости исследуемого
степенного ряда
Пример
5: Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера:
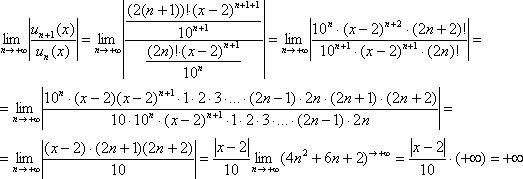 Ответ: Ряд
сходится при
Ответ: Ряд
сходится при ![]()
Почему получилась двойка, а не ноль? Перечитайте классификацию области сходимости степенного ряда. Хотя, наверное, многие уже понимают, почему.
Пример
7: Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера:
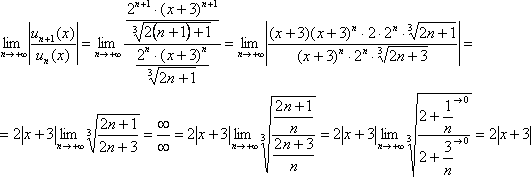 Ряд
сходится при
Ряд
сходится при ![]() Слева
нужно оставить только модуль, умножаем
обе части неравенства на
Слева
нужно оставить только модуль, умножаем
обе части неравенства на ![]() :
:
![]()
![]() В
середине нужно оставить только «икс»,
вычитаем из каждой части неравенства
3:
В
середине нужно оставить только «икс»,
вычитаем из каждой части неравенства
3:
![]()
![]() –
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала:
1)
При
–
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала:
1)
При 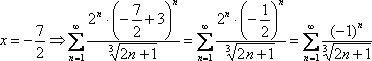 Степень
Степень ![]() сократилась,
значит, мы на верном пути.
Используем
признак Лейбница.
Ряд
является знакочередующимся.
сократилась,
значит, мы на верном пути.
Используем
признак Лейбница.
Ряд
является знакочередующимся.
![]() –
члены ряда убывают по модулю. Каждый
следующий член ряда по модулю меньше,
чем предыдущий, значит, убывание
монотонно.
Ряд
сходится по признаку Лейбница.
Исследуем
ряд на абсолютную сходимость:
–
члены ряда убывают по модулю. Каждый
следующий член ряда по модулю меньше,
чем предыдущий, значит, убывание
монотонно.
Ряд
сходится по признаку Лейбница.
Исследуем
ряд на абсолютную сходимость:
![]() Используем
интегральный признак.
Используем
интегральный признак.
![]() Подынтегральная
функция непрерывна на
Подынтегральная
функция непрерывна на ![]() .
.
![]() Таким
образом, ряд
Таким
образом, ряд ![]() расходится
вместе с соответствующим несобственным
интегралом. Ряд
расходится
вместе с соответствующим несобственным
интегралом. Ряд ![]() сходится
только условно.
2)
При
сходится
только условно.
2)
При 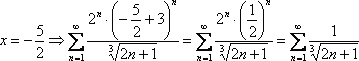 –
расходится (по доказанному).
Ответ: Область
сходимости исследуемого степенного
ряда:
–
расходится (по доказанному).
Ответ: Область
сходимости исследуемого степенного
ряда: ![]() ,
при
,
при ![]() ряд
сходится только условно.
Область
сходимости окончательно можно записать
так:
ряд
сходится только условно.
Область
сходимости окончательно можно записать
так:![]() ,
или даже так:
,
или даже так: ![]() .
Примечание:
Ряд
.
Примечание:
Ряд ![]() можно
было исследовать на сходимость с помощью
предельного признака сравнения.
можно
было исследовать на сходимость с помощью
предельного признака сравнения.
Пример
9: Решение: Найдем
интервал сходимости данного ряда.
Используем признак Даламбера:
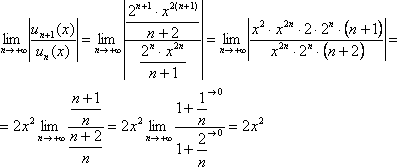 Ряд
сходится при
Ряд
сходится при ![]()
![]()
![]()
![]() –
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала.
1)
При
–
интервал сходимости исследуемого
степенного ряда.
Исследуем
сходимость ряда на концах найденного
интервала.
1)
При 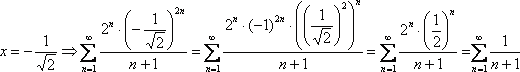 Сравним
данный ряд с расходящимся гармоническим
рядом
Сравним
данный ряд с расходящимся гармоническим
рядом ![]() .
Используем предельный признак
сравнения.
.
Используем предельный признак
сравнения.
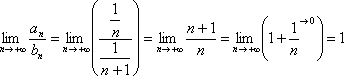 Получено
конечное число, отличное от нуля, значит,
полученный числовой ряд расходится
вместе с гармоническим рядом.
2)
При
Получено
конечное число, отличное от нуля, значит,
полученный числовой ряд расходится
вместе с гармоническим рядом.
2)
При 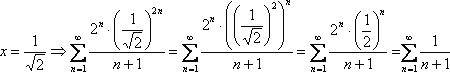 –
расходится (по доказанному).
Ответ: область
сходимости исследуемого степенного
ряда:
–
расходится (по доказанному).
Ответ: область
сходимости исследуемого степенного
ряда: ![]()
