
- •Сверху вниз: упругое тело, левая отсеченная часть, правая отсеченная часть Рис.1. Метод сечений.
- •Эпюры внутренних усилий при растяжении-сжатии
- •Эпюры внутренних усилий при кручении
- •Дифференциальные зависимости между внутренними усилиями при изгибе
- •Напряженное состояние в точке. Тензор напряжений
- •Тензор деформации
- •Потенциальная энергия упругой деформации
- •Механические состояния деформируемых тел
- •Диаграммы упруго-пластического деформирования конструкционных материалов
- •Постановка задач теории надежности
- •Расчетные нагрузки, коэффициенты запаса
- •Расчеты по допускаемым нагрузкам и по допускаемым напряжениям
- •Напряжения при растяжении (сжатии) призматических стержней. Расчет на прочность
- •Понятие о концентрации напряжений, принцип сен-венана
- •Определение деформаций и перемещений
- •Напряженное состояние при растяжении (сжатии)
- •Применение к статически определимым системам.
- •Расчет статически неопределимых систем по способу допускаемых нагрузок.
- •Подбор сечений с учетом собственного веса (при растяжении и сжатии).
- •Деформации при действии собственного веса.
- •Наибольшее и наименьшее значения центральных моментов инерции.
- •Рациональные формы поперечных сечений при изгибе
- •Понятие о составных балках
- •Б) а) несвязанная конструкция, б) связанная сварная конструкция Рис.1. Расчетные схемы составных балок:
- •Дифференциальное уравнение прямого изгиба призматического стержня
- •Расчет валов
- •Понятие о сдвиге. Расчет заклепок на перерезывание.
- •А) расчетная схема, б) действующие усилия Рис.2. Соединение с накладками:
- •90 120 С двумя накладками.
- •А) расчетная схема б) линейное и нелинейное сопротивления Рис.1. Модели изгиба балки:
- •Изгиб балки при действии продольных и поперечных сил.
- •Внецентренное сжатие или растяжение.
- •Примем следующий порядок расчета.
- •3. Строится эпюра крутящего момента Мz.
- •Подбор сечений балок равного сопротивления.
- •Определение деформаций балок переменного сечения.
- •Общие понятия.
- •Расчет бесконечно длинной балки на упругом основании, загруженной одной силой р.
- •Постановка задачи.
- •Вычисление потенциальной энергии.
- •Расчетная модель к теореме Кастильяно.
- •Примеры приложения теоремы Кастильяно.
- •Теорема Максвелла—Мора.
- •Метод Верещагина.
- •А) расчетная схема б)грузовая эпюра в)фиктивное состояние г) эпюра моментов от единичного момента Рис.4. Иллюстрация метода Верещагина:
- •Общие понятия и метод расчета.
- •Способ сравнения деформаций.
- •А) исходная модель, б) фиктивная модель нагружения, в) грузовая эпюра моментов, г) эпюра моментов от реакции в, д) единичная эпюра моментов Рис.2. Решение методом Мора и Верещагина
- •Выбор лишней неизвестной и основной системы.
- •Общий план решения статически неопределимой задачи.
- •Определение деформаций статически неопределимых балок.
- •Связи, накладываемые на систему. Степень статической неопределимости.
- •А) плоская, б) плоскопространственная. В) пространственная Рис.2. Расчетные схемы рамных конструкций:
- •А)внешняя связь, б) две внешние связи в) шесть внешних связей в общем случае Рис.3. Схемы эквивалентных связей
- •А) три внешних связи, б) пять внешних связей Рис.4. Плоская рама
- •А) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей Рис.5. Классификационные признаки рам:
- •А) статически неопределимая — семь, б) — три, в) — четыре, г) — три, е) — двенадцать, ж) — семь, д) — три, и) — тринадцать раз статически неопределима Рис.6. Примеры рамных конструкций:
- •А) , б) и Рис.5. Интерпретация коэффициентов уравнений метода сил:
- •Напряжения в сферических толстостенных сосудах.
- •Диск равного сопротивления.
- •Формула Эйлера для определения критической силы.
- •Влияние способа закрепления концов стержня.
- •Проверка сжатых стержней на устойчивость.
- •Основные характеристики цикла и предел усталости
- •А) растяжение, б) изгиб, в) контактные напряжения Рис.1. Очаги концентрации местных напряжений:
- •Влияние состояния поверхности и размеров детали на усталостную прочность
- •Коэффициент запаса усталостной прочности и его определение
- •Постановка задачи. Явление Резонанса.
- •Влияние резонанса на величину напряжений.
- •Вычисление напряжений при колебаниях.
- •Учет массы упругой системы при колебаниях.
- •Основные положения
- •Общий прием вычисления динамического коэффициента при ударе.
Примем следующий порядок расчета.
1. Разлагаем все внешние силы на составляющие
P1x, P2x,..., Pnx и P1y, P2y,..., Pny.
2. Строим эпюры изгибающих моментов My и My. от этих групп сил.
У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента Mx, и My а целесообразно их заменить результирующим (суммарным) изгибающим моментом (рис. 2)
![]() ,
,
который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси п—п, перпендикулярной вектору Мизг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру Мизг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.
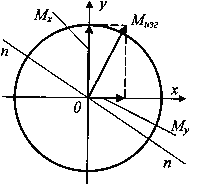 Рис.2.
Формирование результирующего изгибающего
момента
Рис.2.
Формирование результирующего изгибающего
момента
3. Строится эпюра крутящего момента Мz.
Наибольшие напряжения изгиба возникают в точках k и k/, наиболее удаленных от нейтральной оси (рис. 3),
![]() .
.
где Wизг — момент сопротивления при изгибе.
В этих же точках имеют место и наибольшие касательные напряжения кручения
![]() ,
,
где Wр— момент сопротивления при кручении.
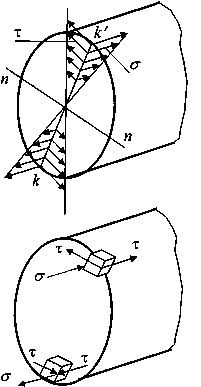 а)
эпюры напряжений б) распределение
напряжений
Рис.3.
Напряженное состояние вала:
а)
эпюры напряжений б) распределение
напряжений
Рис.3.
Напряженное состояние вала:
Как следует из рис. 3, напряженное состояние является упрощенным плоским (сочетание одноосного растяжения и чистого сдвига). Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по критерию Треска—Сен-Венана имеем
![]() .
.
Учитывая, что Wр=2 Wизг, для эквивалентных напряжений получаем
![]() ,
,
где
![]() —эквивалентный
момент, с введением которого задача
расчета вала на совместное действие
изгиба и кручения, сводится к расчету
на эквивалентный изгиб.
—эквивалентный
момент, с введением которого задача
расчета вала на совместное действие
изгиба и кручения, сводится к расчету
на эквивалентный изгиб.
Аналогично для Мэкв по.критерию Губера—Мизеса получаем
![]()
Тогда условие прочности для вала из пластичного материала будет иметь вид
![]() .
.
Для стержня из хрупкого материала условие прочности следует записать в виде
![]() ,
,
где Мэкв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора
![]()
где
![]() .
.
Обратим внимание на особенности расчета при сочетании изгиба, растяжения и кручения стержня прямоугольного поперечного сечения (рис. 4.) Для выявления опасной точки здесь должны быть сравнены напряжения косого изгиба с растяжением в точке А, с эквивалентными напряжениями в точках В и С.
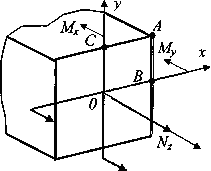 Рис.4.
Модель расчета напряжений при сочетании
кручения, растяжения и изгиба.
Рис.4.
Модель расчета напряжений при сочетании
кручения, растяжения и изгиба.
Полученные соотношения приобретают крайнюю необходимость и востребованность при выполнении Вами курсового проекта по основам конструирования при расчете на прочность и жесткость валов передач.
Лекция № 30. Расчет балок переменного сечения.
Подбор сечений балок равного сопротивления.
Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.
Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.
Так
как изгибающие моменты обычно меняются
по длине балки то, подбирая ее сечение
по наибольшему изгибающему моменту, мы
получаем излишний запас материала во
всех сечениях балки, кроме того, которому
соответствует
![]() .
Для экономии материала, а также для
увеличения в нужных случаях гибкости
балок применяют балки
равного сопротивления.
Под этим названием подразумевают балки,
у которых во всех сечениях наибольшее
нормальное напряжение одинаково и
должно быть равно допускаемому.
.
Для экономии материала, а также для
увеличения в нужных случаях гибкости
балок применяют балки
равного сопротивления.
Под этим названием подразумевают балки,
у которых во всех сечениях наибольшее
нормальное напряжение одинаково и
должно быть равно допускаемому.
Условие, определяющее форму такой балки, имеет вид
![]()
и
![]()
Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.
Эти
условия справедливы и для сечения с
наибольшим изгибающим моментом; если
обозначить
![]() —
момент сопротивления балки в сечении
с наибольшим изгибающим моментом
—
момент сопротивления балки в сечении
с наибольшим изгибающим моментом
![]() ,
то можно написать:
,
то можно написать:
|
|
(1) |
Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.
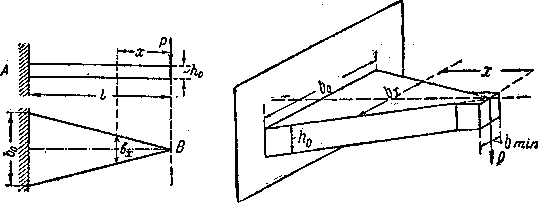 Рис.1.
Расчетная схема балки равного сопротивления
Рис.1.
Расчетная схема балки равного сопротивления
Пусть
высота балки будет постоянной
![]() ,
а ширина переменной—
,
а ширина переменной—![]() .
Момент сопротивления в сечении на
расстоянии х
от свободного конца будет
.
Момент сопротивления в сечении на
расстоянии х
от свободного конца будет
![]() ,
а изгибающий момент
,
а изгибающий момент
![]() ;
момент сопротивления опорного сечения
;
момент сопротивления опорного сечения
![]() ,
a наибольший изгибающий момент в опорном
сечении
,
a наибольший изгибающий момент в опорном
сечении
![]() .
В расчете имеют значения лишь абсолютные
величины М(х)
и
.
В расчете имеют значения лишь абсолютные
величины М(х)
и
![]()
По формуле (1) получаем:
![]()
откуда
![]()
т.
е. ширина меняется по линейному закону
в зависимости от х.
При
![]() ширина
равна
ширина
равна
![]() .
.
Вид
балки в фасаде и плане показан на Рис.1.
Такое очертание балки получается, если
учитывать ее прочность только по
отношению к нормальным напряжениям;
ширина
![]() в
сечении В
обращается в нуль.
в
сечении В
обращается в нуль.
Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения
![]()
или,
так как
![]()
![]()
Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.
