
ПОСОБИЕ ЧАСТЬ 2 -цепи переменного тока
.pdf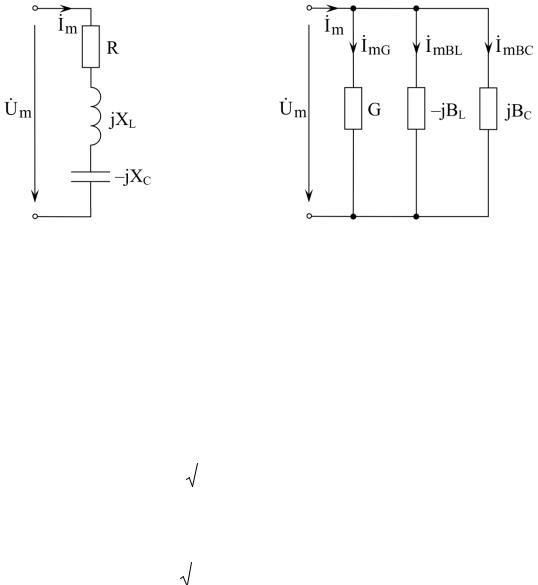
Рис. 1.3 |
Рис. 1.4 |
n |
n |
Z Zk R jXL jXC R jX, |
Y Yk G jBL jBC G jB. |
k=1 |
k=1 |
Здесь XL L; XC 1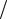 C; X XL XC; BL 1
C; X XL XC; BL 1 L; BC C; B BL BC.
L; BC C; B BL BC.
Формулы для преобразования последовательной цепи в параллельную и для выполнения обратного преобразования, для случая активно-индуктивной реакции цепи, имеют вид:
Y |
1 |
|
1 |
|
|
|
|
|
|
R |
j |
|
X |
|
|
|
R |
j |
|
|
X |
|
G jB; |
|
||||||||||||||||
|
|
|
|
|
|
R |
2 X2 |
R |
2 X2 |
|
R2 X2 |
R2 X2 |
|
|||||||||||||||||||||||||||
|
|
Z R jXL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
XL |
XC |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
G=R/Z |
|
|
|
; |
|
|
|
Y G2 B2 ; |
|
|
B=X/Z |
|
|
|
|
BL BC |
; |
|||||||||||||||||||||||
R2 X2 |
|
|
|
|
|
Z2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
G |
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
j |
|
R + jX; |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
G2 B2 |
G2 B2 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Y G jB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
R |
G |
|
|
|
|
G |
; |
|
|
|
|
|
|
|
|
|
|
X |
B |
|
BL BC |
XL XC. |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Z |
R2 X2 |
; |
|
|
|
|
||||||||||||||||||||||||
Y2 |
G2 B2 |
|
|
|
|
|
|
|
|
|
|
G2 B2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y2 |
|
|
|
|
|||||||||||||
(здесь G и B – соответственно активная и реактивная проводимости; R и X – активное и реактивное сопротивления).
Замечание: необходимо помнить, что взаимообратными являются лишь комплексы Z и Y , а их составляющие R и G, X и B не являются таковыми.
О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока.
Законы Ома и Кирхгофа относятся к универсальным законам, т.к. они основываются на фундаментальном законе природы – законе сохранения энергии, поэтому законы Ома и Кирхгофа могут быть использованы при расчете цепей постоянного и переменного тока, как для мгновенных, так и для комплексных (векторных) параметров.
1.3 Мощность в цепи синусоидального тока
Комплексная полная мощность цепи переменного тока определяется как:
. .
S UI UIcos + jUIsin P+ jQ Se j ,
11
где |
S UI P2 Q2 |
ZI2 ВА, |
P = UIcos Scos RI2 Вт, |
Q= UIsin Ssin XI2 |
ВАр. |
|
|
Дополнительные единицы измерений [S] = кВА, МВА, mВА, μВА; [P] = кВт, МВт, mВт, μВт; [Q] = кВАр, МВАр, mВАр, μВАр.
Баланс мощностей:
n . |
|
. |
|
n |
2Rk Ik2j XLk XCk , |
Ek Ik Uk Jk Ik |
|||||
|
|
|
|
k=1 |
|
k=1 |
|
|
|
. |
|
. |
|
|
|
|
|
где Uk – напряжение на зажимах источника тока Jk.
1.4 Треугольники токов, напряжений, сопротивлений, проводимо-
стей и мощностей
.
Так как токи (U, Z, Y, S) в символическом методе представляются в ви-
де комплексов, то, отложив вдоль действительной оси комплексной плоскости
.
активную составляющую тока (U, Z, Y, S), а вдоль мнимой оси – реактивную
.
составляющую, получим треугольник токов (U, Z, Y, S), который дает графическую интерпретацию связи между модулем и его активной и реактивной составляющими. На рис. 1.5.а и 1.5.б приведены треугольники напряжений и сопротивлений, токов и проводимостей для RL – цепи, а на рис. 1.6 – треугольники сопротивлений и проводимостей, совмещенные с треугольниками мощностей.
а) б)
|
Рис. 1.5 |
а) |
б) |
Рис. 1.6
12

1.5 Векторные и топографические диаграммы
Векторной диаграммой называется совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной частоты, построенных с соблюдением сдвига их относительно друг друга по фазе. Аналитические расчеты электрических цепей синусоидального тока следует сопровождать построением векторных диаграмм, чтобы иметь возможность качественной оценки и контроля этих расчетов.
Совокупность точек комплексной плоскости, изображающих комплексные потенциалы одноименных точек схемы, называется топографической диаграм-
мой. По топографической диаграмме можно определить напряжение между лю-
.
быми точками схемы. Так, например, вектор напряжения Uab на топографической диаграмме между точками "a" и "b" будет направлен в точку первого индекса, т.е от "b" к "a".
Общее замечание: не следует полностью отождествлять комплексный ток (напряжение) с реальным током, протекающим в цепи (напряжением, действующем на участке цепи). Необходимо помнить, что комплексные величины – это изображения реальных функций времени, поэтому, наряду с комплексными величинами, нужно записывать мгновенные значения этих величин.
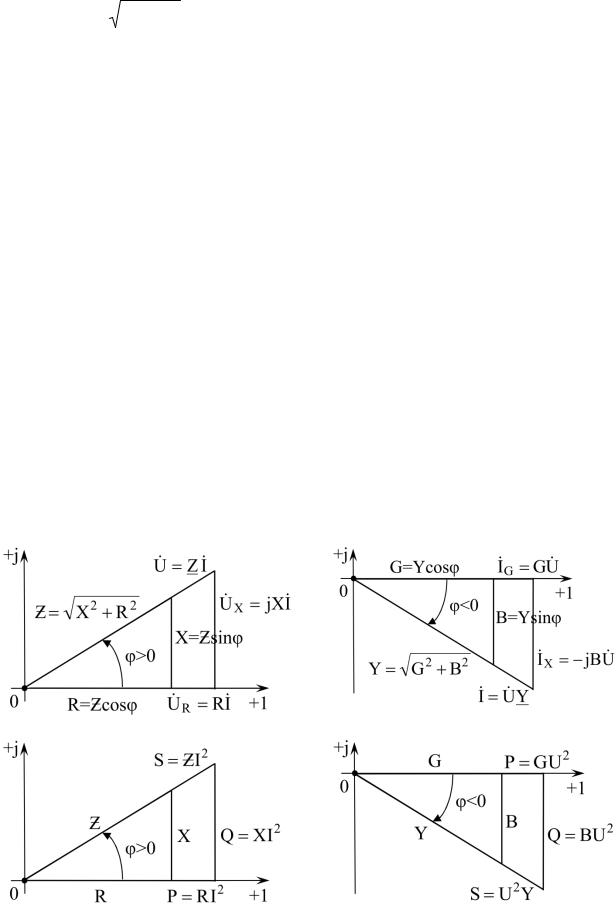
1.6 Последовательное соединение R–L–C элементов
Рис. 1.7 |
Рис. 1.8 |
Для схемы, представленной на рис. 1.7, справедливы следующие соотношения, записанные для мгновенных (временных) и комплексных функций.
Мгновенные
u(t) uR(t) uL(t) uC(t);
uR(t) i(t)R;
uL(t) Ldi(t); dt
uC(t) C1 i(t)dt;
|
. |
Комплексные |
. |
|
||
|
. |
. |
|
|||
|
Um URm ULm UCm; |
|
||||
|
|
. |
. |
|
|
|
. |
|
URm RIm; |
. |
|
||
|
. |
. |
|
|||
ULm j LIm jXL Im ZL Im; |
|
|||||
. |
1 . |
1 . |
. |
. |
||
UCm j |
|
Im |
|
Im jXC Im ZC Im . |
||
C |
|
|||||
|
|
j C |
|
|
||
13
где |
|
L 1 C |
– угол сдвига по фазе между полным комплексным |
||
arctg |
|
|
|||
R |
|||||
|
|
|
. |
||
|
|
. |
|
||
напряжением Um и комплексным током Im. Векторная диаграмма для последовательного соединения R–L–C элементов представлена на рис. 1.8.
Комплексное сопротивление для схемы, представленной на рис. 1.7: Z R jX R j(XL XC) R j L 1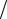 C Z ej =Zcosφ + jZsinφ,
C Z ej =Zcosφ + jZsinφ,
|
|
|
|
|
|
L 1 C |
|
где R = Zcosφ, X = Zsinφ, Z R |
2 |
|
2 |
||||
|
(XL XC) |
|
, arctg |
|
. |
||
|
|
R |
|||||
|
|
|
|
|
|
|
|
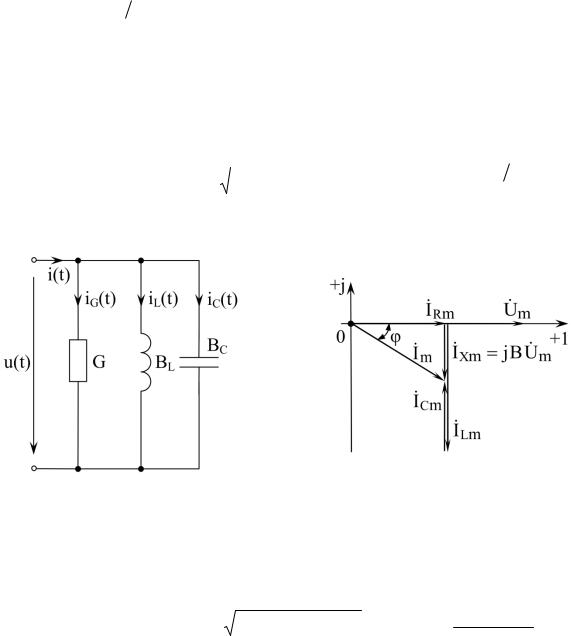
1.7 Параллельное соединение R–L–C элементов
Рис. 1.9 |
Рис. 1.10 |
ВД для параллельного соединения R–L–C элементов (рис. 1.9) представлена на рис. 1.10.
Комплексная проводимость для схемы, представленной на рис. 1.9:
Y G jB R j(BL BC) G j 1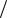 L C Yej Ycos jYsin ,
L C Yej Ycos jYsin ,
где G Ycos , B Ysin , Y G2 (BL BC)2 , arctg 1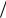 L C .G
L C .G
1.8 Резонанс в электрических цепях
Резонансом называется такой режим работы пассивной электрической цепи, при котором ее полное эквивалентное комплексное сопротивление (проводимость) содержит только вещественную часть, то есть, оказывается чисто активным, а входной ток совпадает по фазе с входным напряжением.
1.8.1Резонанс напряжений
Всоответствии с определением резонанса в электрической цепи, резонанс напряжений возникает при последовательном соединении R, L ,C – элементов вследствие равенства на частоте ω0 реактивных сопротивлений (рис. 1.11).
14

Рис. 1.11
Такую цепь называют последовательным колебательным контуром, а ус-
ловия резонанса для него имеют вид:
1) Z R j L 1 C R jX0 R;
C R jX0 R;
2) XL0 0L XC0 |
|
1 |
|
L |
; |
0C |
|
||||
|
|
|
C |
||
3)X0 XL0 XC0 0L 1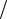 0C 0;
0C 0;
4)UL0 IXL0 I 0L UC0 IXC0 I 1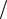 0C ;
0C ;
5) |
X0 |
|
|
0L 1 0C |
0, где 0 |
|
|
|
|||
1 LC. |
|||||||||||
arctg |
|
|
arctg |
|
|
||||||
R |
R |
||||||||||
|
|
|
|
|
|
|
|
|
|||
Отношение падения напряжения на индуктивности (UL0) или падение напряжения на емкости (UС0) к общему напряжению (U), приложенному ко всей R, L, C – цепи на резонансной частоте ω0 называется коэффициентом резонанса или добротностью резонансного контура:
Q UL0 UC0 I 1 
 L. U U RI R R
L. U U RI R R  C
C
Добротность показывает, во сколько раз падение напряжения на индуктивности или емкости при резонансе больше, чем напряжение, приложенное ко всей R, L ,C – цепи, то есть добротность характеризует перенапряжения на реактивных элементах контура при резонансе.
1.8.2 Энергетические процессы при резонансе
Мгновенные мощности катушки индуктивности и конденсатора: pL(t) = ULI sin 2ωt и pС(t)= – UСI sin 2ωt
при резонансе, когда UL = UС, в любой момент времени равны и противоположны по знаку. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, причем обмен энергией между L – C элементами и источником энергии, питающим цепь, не происходит:
W = WL + WC = LI2Cm = CU2Cm= const,
т.к сумма энергий магнитного и электрического полей с течением времени не изменяется:
WL WC LI2m CU2m const. 2 2
Если энергия электрического поля максимальна, то энергия магнитного поля равна нулю, и наоборот. Источник энергии, питающий цепь, только покрывает расход энергии в активном сопротивлении R контура.
15

1.8.3 Резонанс токов
Этот резонанс возможен на участке цепи, содержащем параллельное соединение индуктивного и емкостного элементов. Такую цепь часто называют
параллельным колебательным контуром. Если параллельные ветви контура со-
держат активные сопротивления, то их называют реальными параллельными контурами (рис. 1.12 и 1.13).
Рис. 1.12 |
Рис. 1.13 |
В соответствии с определением резонанса, в параллельном контуре он будет иметь место, если:
1) Y Y1 Y2 |
|
1 |
|
1 |
|
1 |
|
1 |
GL GC; |
|
|
|
RL jXL |
RC jXC |
|||||||
|
|
Z Z |
2 |
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
||
2) BL |
L |
BC |
|
1 C |
; |
|
|
|
RL2 ( L)2 |
RC2 1 C 2 |
|
|
|
||||
3)B BL BC 0; 4)IL0 UBL0 |
U 0L |
|
IC0 UBC0 |
U C |
; |
|||
RL2 ( 0L)2 |
RC2 1 C 2 |
|||||||
5)arctg BL0 BC0 0.
G1 G2
ВД для реального параллельного контура изображена на рис. 1.14. Здесь I1
=IGL + IBL = IGL – jIBL, а I2 =IGС + IBL = IGС + jIBL.
Рис. 1.14 |
Рис. 1.15 |
16
Резонансная частота реального параллельного контура находится из усло-
вия:
|
|
|
|
|
0L |
|
|
|
|
|
|
1 0C |
|
|
|
|
|||||
BL0 |
|
|
|
|
|
|
BC0 |
|
|
|
|
, |
|||||||||
RL2 ( 0L)2 |
RC2 1 0C 2 |
||||||||||||||||||||
и определяется, как: |
|
|
|
1 |
|
|
L C RL |
2 |
|
|
|
|
2 RL |
2 |
|
, |
откуда следует, что |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
р |
|
|
|
LC L C RC2 |
0 |
|
2 RC2 |
|
|
|
||||||||||
активные сопротивления реальных параллельных ветвей оказывают влияние на резонанс в параллельном контуре.
Для получения резонанса RL2 и RС2 должны быть одновременно или боль-
ше, или меньше |
2 |
|
L |
2 |
|
2 |
|
2 |
|
|
|
|||
|
|
. При RL |
RC |
|
|
|
, существует единственная частота, |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
на которой возникает резонанс токов: р 1 |
|
LC |
0. |
|||||||||||
При RL |
2 RC |
2 |
2 |
резонанс токов наблюдается на любой частоте, а при |
||||||||||
RL2>ρ2 и RС2<ρ2 или RL2<ρ2 и RС2>ρ2 резонанс в параллельном контуре не возникает.
В идеальном параллельном контуре RL=0 и RС=0. Это значит, что в схеме замещения GL и GC будут отсутствовать, а BL0 и BC0 будут зависеть только от частоты и L – C параметров:
BL0 1 0L, |
|
BC0 |
1 |
|
0C. |
|||
|
1 0C |
|||||||
|
|
|
|
|
|
|
||
В этом случае IGC = IGL = 0 и, так как при резонансе токов IC0 = IL0, входной |
||||||||
ток идеального параллельного контура будет равен нулю: |
|
|||||||
I = (IGС + IGL) + j(–IL0 + IС0) = 0. |
|
|
|
|||||
Это значит, что входное сопротивление идеального параллельного контура |
||||||||
бесконечно велико: |
|
|
|
|
|
|
||
ZВХ |
1 |
|
1 |
|
. |
|
|
|
|
j(BL0 |
|
|
|
|
|||
|
Y |
BC0) |
|
|
|
|||
ВД для этого случая изображена на рис. 1.15. Токи в параллельно включенных элементах, находящихся под общим напряжением, равны по величине, противоположны по знаку и взаимно компенсируют друг друга, вследствие чего входной ток:
I = IС + IL = 0.
Тогда собственная резонансная частота идеального параллельного контура может быть найдена как: от 1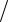

 LC, отсюда следует, что ωот определяется, подобно резонансной частоте последовательного колебательного контура
LC, отсюда следует, что ωот определяется, подобно резонансной частоте последовательного колебательного контура
( он).
Отношение:
Q |
IL0 |
|
IC0 |
|
U |
|
|
|
|
U(R1 R2) |
(R1 R2) |
||||
|
U U |
|
|||||
17
называется добротностью параллельного контура, а величина d = 1/Q' называется затуханием параллельного контура.
При резонансе в реальном параллельном контуре сумма энергий электрического и магнитного полей не остается постоянной. Она постоянна лишь в теоретическом случае при RL = RС = 0, то есть в идеальном параллельном контуре.
1.9 Резонанс в сложных цепях
Если в сколь угодно сложной электрической цепи реактивные составляющие сопротивлений или проводимостей схемы обращается в нуль (X = 0, B = 0), то это служит свидетельством резонансных явлений в разветвленных цепях. Количество резонансных частот определяется числом разнородных L – C элементов и способом их соединения.
Условия резонанса напряжений X XL XC 0 и резонанса токов B BL BC 0 остаются справедливыми и для разветвленных электрических цепей. В целях упрощения частотного анализа таких цепей можно использовать мнемоническое правило, основанное на условиях резонанса токов и резонанса напряжений, а также на зависимости реактивных сопротивлений XL L и XC 1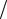 C от частоты.
C от частоты.
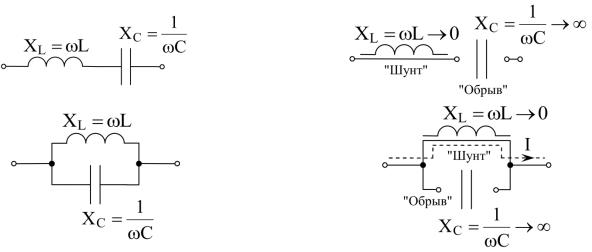
Так, при ω = 0 (на постоянном токе), реактивное индуктивное сопротивление в установившемся режиме обращается в нуль – XL L 0 L 0 (превращается в "шунт"), а реактивное емкостное сопротивление стремится в бесконечность – XC 1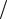 C 1
C 1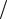 0 C , что эквивалентно "обрыву" цепи. В этом случае последовательный и параллельный контура приводятся к виду:
0 C , что эквивалентно "обрыву" цепи. В этом случае последовательный и параллельный контура приводятся к виду:
а) |
Если 0 |
б) |
Если 0 |
Рис. 1.16
Если частота источника питания ω = 0, то это будет источник постоянной ЭДС, следовательно, для характеристики электромагнитных процессов в цепи при ω = 0 можно использовать понятие "постоянный ток – I". Тогда, мнемоническое правило можно сформулировать следующим образом:
18
Если в разветвленной (или последовательно-параллельной) электрической цепи есть контур для протекания постоянного тока, то первым по частоте, изменяющейся от 0 до ∞, будет резонанс токов (рис. 1.16.б).
Если в разветвленной (или последовательно-параллельной) электрической цепи контура для прохождения постоянного тока нет, то первым по частоте, изменяющейся от 0 до ∞, будет резонанс напряжений (рис. 1.16.а).
Применяя мнемоническое правило для разветвленных электрических цепей, представленных на рис. 1.17 – 1.18, получим, что в схеме на рис. 1.17 первым по частоте, изменяющейся то 0 до ∞ будет резонанс токов, а вторым – резонанс напряжений. В схеме, представленной на рис. 1.18 первым по частоте будет резонанс напряжений, а вторым резонанс токов. Это связано с тем, что в схеме на рис 1.17 есть контур для протекания постоянного тока, а в схеме на рис. 1.18 такого контура нет.
Рис. 1.17 |
Рис. 1.18 |
Для доказательства приведенного выше утверждения найдем входное сопротивление для схемы, приведенной на рис. 1.17.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
j2 L1 |
|
|
|
|
||||
|
|
|
|
ZL2ZC1 |
|
|
|
|
j L1 |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Z Z |
L1 |
|
|
|
|
j L2 |
|
|
|
|
|
|
|
|
|
|
|
j L2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Z |
|
Z |
|
|
|
|
|
|
j |
|
|
|
2 |
|
|
|
||||||||||||||||||
вх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
L2 |
C1 |
|
|
|
|
j |
L1 |
|
|
|
|
|
|
|
|
|
|
L1C1 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
C1 j |
C1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
j L2 j |
|
|
|
|
|
|
j L2 |
|
|
|
|
|
|
|
|
|
jX . |
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
(j ) ( L1C1 |
1) |
|
|
|
|
L1C1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
При резонансе токов |
B 0 |
|
или X 1 B , |
|
поэтому примем, |
|
что |
|||||||||||||||||||||||||||
2L1C1 1 0, тогда X 0, а резонансная частота для параллельного контура будет равна:
от 1

 L1C1.
L1C1.
При резонансе напряжений X 0, поэтому приравниваем к нулю всю квадратную скобку уравнения входного сопротивления (Zвх):
L1
L2 2L1C1 1 0.
Приведем все к общему знаменателю, а затем умножим на общий знаменатель левую и правую части тождественного равенства, после чего, получившееся выражение разделим на ω:
19
L2 2L1C1 1 L1 0|: , тогда: L2 2L1C1 1 L1 0,
откуда, раскрывая скобки и группируя подобные, получим:
2L1L2C1 L1 L2 0,
Из последнего выражения находим частоту, при которой в разветвленной цепи будет резонанс напряжений:
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 L2 |
|
1 |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
он |
|
|
L1L2C1 L1C1 |
|
|
|
|
L2C1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
Сопоставляя резонансные частоты от и |
|
|
он, получим, что |
от < он, |
||||||||||||||||||||||||||||||||||
что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
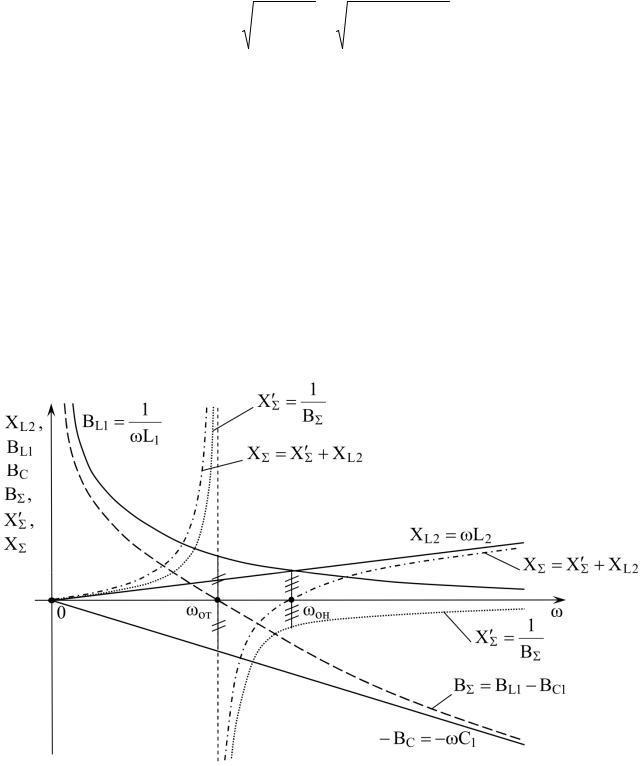
|
Задавая ряд значений частоты источника питания в диапазоне от 0 до ∞, |
||||||||||||||||||||||||||||||||||||||
можно построить частотные характеристики (см. рис. 1.19) отдельных элементов |
|||||||||||||||||||||||||||||||||||||||
и всей схемы, представленной, например, на рис. 1.17. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ω |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
BC1 |
|
|
C1 |
|
B |
|
BL |
|
BC |
|
|
|
|
|
|
|
|
|
|
XL2 |
L2 |
X |
|
X |
|
XL2 |
|||||
|
BL1 L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
B |
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
+ ∞ |
|
|
0 |
|
|
|
|
|
+ ∞ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|||||||||
от |
1 |
|
|
|
|
|
отC1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
± ∞ |
|
|
отL2 |
|
|
± ∞ |
|
||||||||||||
|
|
отL1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
онC1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
XL2 |
||||||||
он |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
онC1 |
|
|
|
|
|
|
|
|
онL2 |
|
X |
|
|||||||||||
|
|
онL1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
онL1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∞ |
0 |
|
|
|
|
|
– ∞ |
|
|
|
|
|
– ∞ |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
∞ |
|
|
∞ |
|
|
|||||||
Рис. 1.19
Для схемы, представленной на рис. 1.18 справедливы аналогичные рассуждения. Выполнить самостоятельно.
20
