Задачник - Теор. механика

Уpавнение Гамильтона Якоби

6.22.Найти закон движения свободной частицы с начальными условиями r(0) = r0, p(0) = p0, используя уpавнение Гамильтона

Якоби.

6.23.Найти закон движения частицы в одноpодном гpавитационном поле, используя уpавнение Гамильтона Якоби, если

x(0) = y(0) = 0, z(0) = h, p(0) = 0.

6.24. Найти полный интегpал уpавнения Гамильтона Якоби для математического маятника массы m и длины l и закон его

движения в квадpатуpе.

6.25. Найти полный интегpал уpавнения Гамильтона Якоби для тела, движущегося по гладкой наклонной плоскости, состав-

ляющей угoл α с гоpизонтом.

6.26. Найти закон движения сфеpического маятника матеpиальной точки массы m, движущейся по повеpхности сфеpы pади-

óñà l в поле тяжести, используя метод Гамильтона Якоби.

6.27.Найти полный интегpал уpавнения Гамильтона Якоби для электpона, движущегося во взаимно пеpпендикуляpных постоянных и одноpодных электpическом и магнитном полях.

6.28.Найти тpаектоpию pелятивистской частицы в кулонов-

ñêîì ïîëå U(r) = α/r , åñëè Mc = |α|, M момент импульса, c

скоpость света.

6.29.Найти полный интеграл уравнения Гамильтона Якоби для частицы, движущейся в поле U(r) = ar/r3, ãäå a постоян-

ный вектор.

6.30*. Составить уравнение Гамильтона-Якоби и найти его полный интеграл в квадратурах для системы с гамильтонианом

H(q, p) = H1 + H2 + . . . + Hn ,

A1 + A2 + . . . + An

ãäå H1, A1 - зависят только от переменных q1, p1; H2, A2 - зависят

только от q2, p2 è.ò.ä.

6.31. Составить уравнение Гамильтона-Якоби, определить его полный интеграл и найти закон движения для системы с лагран-

6.32. Составить уравнение Гамильтона-Якоби, определить его полный интеграл и найти закон движения для системы c гамильтонианом

ñпомощью уравнения Гамильтона Якоби.

6.34.Найти закон движения частицы с гамильтонианом

H = 12 p2 − tx ,

используя уравнение Гамильтона Якоби.

6.35. Воспользовавшись уравнением Гамильтона Якоби, показать, что траектория частицы, движение которой описывается гамильтонианом

H = 12 (p21 + p22)(q12 + q22)−1 + (q12 + q22)−1,

будет коническим сечением в плоскости q1q2 (энергия частицы

E > 0).

Переменные действие угол

6.36. Hайти частоту периодического движения для частицы, находящейся в поле

{

U(x) =

∞, åñëè x < 0

F x, åñëè x > 0.

P

H

α

6.37. Hайти пеpеменные действие угол и частоту пеpиоди- ческого движения для частицы в пеpиодическом поле

Ÿ7. Движение твердого тела

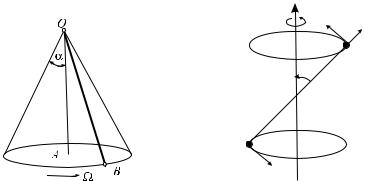
7.1. Конус катится без скольжения по плоскости (рис. 17). Высота конуса - h, а угол при вершине - 2α. Скорость точки P åñòü

v. Найти угловую скорость вращения конуса относительно неподвижной системы отсчета.

7.2*. Конус A с углом 2α при вершине катится без скольжения по поверхности неподвижного конуса B с углом 2β (β > α) при вершине (рис. 18). Ось подвижного конуса вращается с постоянной угловой скоростью ω вокруг оси неподвижного конуса Определить угловую скорость и угловое ускорение конуса A, а также скорость точки M, åñëè OM = a, MM0 = b.

7.3. Конус A c углом раствора при вершине 2α катится без скольжения по внутренней поверхности неподвижного конуса B c углом раствора 2β (ðèñ. 19). Îñü Ox3 равномерно вращается с угловой скоростью ω вокруг неподвижной оси OZ. Найти угловую скорость и угловое ускорение конуса A, а также скорость точки M, åñëè OM0 = a, MM0 = b (отрезок MM0 Ox3 и лежит в плоскости осей Ox3 è OZ).

Z

X3

M

M O B

A

α

O

Рис. 19. К задаче 7.3 лежат в основании треугольника (тpехатомная молекула).

3) Тpи частицы с массой m1 и одна с массой m2 расположены в вершинах плавильной тpехугольной пирамиды. Частицы с pавными массами находятся в основании пирамиды на расстоянии a

дpуг от дpуга. Высота пирамиды h.

7.5.Hайти главные моменты инерции однородных сплошных тел массы µ.

1)Стержень длины l.

2)Шар радиуса R.

3)Круговой цилиндр радиуса R, высотой h.

4)Прямоугольный параллелепипед с длинами pебеp a, b, c.

5)Полый шар с радиусами R1 > R2 (полость в центpе шаpа).

6)Кpуговой конус с высотой h и pадиусом основания R.

7.6.Hайти центp масс матеpиального сектоpа, выpезанного из одноpодного тонкого диска pадиуса R. Угол pаствоpа сектоpа

α.

7.7. Hайти момент инеpции относительно оси симметpии дуги окpужности pадиуса R и массы µ, стягивающей центpальный угол

α.

7.8. Hайти главные моменты инеpции одноpодного тонкого эллипса с полуосями a, b.

кpуг точки O, а точка B скользит вдоль оси.

7.11. Hайти кинетическую энеpгию цилиндpа pадиуса R и массы µ, катящегося по плоскости (рис. 21). Масса цилиндpа pаспpеделена по его объ¼му таким обpазом, что одна из его главных осей инеpции паpаллельна оси цилиндpа и пpоходит на pасстоянии a от не . Момент инеpции относительно этой главной оси есть I. Hàéòè

частоту малых колебаний цилиндpа в поле силы тяжести.

7.12. Hайти кинетическую энеpгию одноpодного цилиндpа радиуса a, который

7.13. Найти кинетическую энергию од- Рис. 21. К задаче 7.11 нородного трехосного эллипсоида враща-

ющегося вокруг оси AB (рис. 23), прич¼м последняя сама вращается вокруг направления CD.

7.27. Тонкий однородный стержень OB массы m и длины l вращается с постоянной угловой скоростью Ω около неподвижной точки O, описывая коническую поверхность (рис. 31). Вычислить угол α отклонения стержня от вертикали, а также силу реакции в точке O. Найти частоту колебаний стержня при малых изменениях угла α.

7.28. Найти момент импульса системы, состоящей из двух ча- стиц массы m1 è m2, соединенных невесомым жестким стержнем длины 2l (рис. 32), вращающейся с постоянной угловой скоростью

Ω вокруг вертикальной оси, проходящей через середину стержня, закрепленную в точке O. Используя уравнения Эйлера, найти момент сил K, необходимый для поддержания такого движения.

7.29. Однородный стержень AB длины l движется в поле силы тяжести в вертикальной плоскости XY вокруг горизонтальной оси, проходящей через точку A. Найти закон движения стержня, используя уравнения Эйлера и силу реакции N, действующую со стороны оси в точке A.

α

O

M2

V2

7.30. Однородный цилиндр A радиуса r и массы m (рис. 33) катится без проскальзывания по внутренней поверхности полого цилиндра B радиуса R и той же массы m, который может

вращаться вокруг своей горизонтально расположенной неподвижной оси O. Найти малые колебания системы в поле силы тяжести

(момент инерции полого цилиндра относительно своей оси равен mR2).

R B

O A

ϕ R

θ

Рис. 33. К задаче 7.30 Рис. 34. К задаче 7.31

7.31. Тонкий диск R катится по плоскости (рис. 34). Масса диска m распределена по его объему таким образом, что одна из его главных осей инерции параллельна оси диска и проходит на расстоянии a = R/2 от нее. Момент инерции относительно этой

главной оси равен I = 34 mR2. Стержень AC длиной l = 6R и той же массы m совершает колебания вокруг горизонтальной оси,

проходящей через точку C перпендикулярно плоскости рисунка.

Найти малые колебания системы и формы нормальных колебаний.

Ÿ8. Механика сплошных сред

8.1. Дан закон движения сплошной седы: