Panin_M_P_Modelirovanie_perenosa_izluchenia

ЧАСТЬ 2. МЕТОД МОНТЕ-КАРЛО В ЗАДАЧАХ ПЕРЕНОСА ИЗЛУЧЕНИЯ

Глава 6. Основы метода Монте-Карло

Мы все учились понемногу Чему-нибудь и как-нибудь… А.С. Пушкин

Общепринятого определения метода Монте-Карло нет. Чаще всего так называют численные методы решения математических задач при помощи моделирования случайных величин.

Моделирование случайных величин означает воспроизведение на компьютере модели реального явления, имеющего случайную природу. Например, компьютер может имитировать карточную игру. Или довольно часто на компьютерах получают синтетические данные измерений, которые выглядят как настоящие. Такие данные используются при тестировании работы различных систем, предназначенных для их обработки.

Обратим внимание на то, что в приведенном выше определении метода Монте-Карло целью моделирования случайных величин является получение некоторого математического результата. Важнейший прием этого метода есть приведение решаемой задачи к расчету математических ожиданий. В этой связи имитация на компьютере карточной (а также любой другой азартной) игры или экспериментальных результатов не относится к методам Монте-Карло.

§6.1. Краткий очерк истории метода Монте-Карло

Название Монте-Карло было впервые использовано для класса математических методов группой ученых (Дж. Фон Нейман, Э. Ферми, С. Улам, Н. Метрополис), работавших в начале 40-х годов XX века в лаборатории Лос-Аламос (США) над созданием ядерного оружия. Существо метода заключалось в применении случайных чисел для решения математических задач. Поскольку к случайным числам имеют непосредственное отношение все азартные игры, имя новому методу было дано по

65

названию небольшого городка в княжестве Монако, известного своими игорными домами.

Первое упоминание о математическом методе с таким названием относится к 1949 году. Станислав Улам, находясь дома из-за болезни, в течение нескольких дней развлекался раскладыванием пасьянса. Задавшись целью определить вероятность того, что пасьянс сойдется, он сделал безуспешную попытку вычислить ее с помощью методов комбинаторики. После этого ему пришла в голову мысль, что вероятность такого сложного события проще установить экспериментально, разложив большое количество пасьянсов и подсчитав процент успешных исходов.

Однако самое раннее использование случайных событий для вычисления математических величин принадлежит, по-видимому, графу Де Бюффону. Он в 1777 году описал эксперимент со случайным бросанием иголки на горизонтальную поверхность, расчерченную параллельными прямыми. Граф показал, что если расстояние d между линиями больше длины иголки L, то вероятность того, что иголка пересечет линию P = 2Lπ d .

Позднее (в 1886 году) Лаплас предложил применить этот эксперимент для нахождения числа π. По существу, это было первым использованием метода Монте-Карло: с помощью моделирования случайного процесса вычислялась математическая величина. В 1901 году один из основоположников термодинамики лорд Кельвин с помощью случайных чисел оценивал некоторые интегралы в кинетической теории газов.

Интенсивное развитие самого метода Монте-Карло, как и его практическое использование, началось после Второй мировой войны вместе с появлением производительных вычислительных машин.

В настоящее время данный метод – один из наиболее распространенных для решения задач переноса излучений. Его преимуществом является способность решать сложные трехмерные нестационарные задачи, не внося никаких упрощений в физическую модель взаимодействия излучения с веществом. Он требует относительно небольшого объема оперативной памяти компьютера и хорошо приспособлен для параллельных вычислений.

66

Результаты, полученные методом Монте-Карло, носят, однако, статистический характер, а скорость их сходимости – низкая. В этом причина того, что на стационарных задачах с малой размерностью метод Монте-Карло проигрывает по эффективности обычным численным методам.

Метод Монте-Карло основан на использовании случайных величин, он широко прменяет базовые понятия теории вероятностей и математической статистики. Их следует вспомнить, прежде чем познакомиться с самим методом.

§6.2. Случайные величины

Случайной величиной называют любую количественную характеристику опыта, которая при его неоднократном воспроизведении непредсказуемо принимает одно из ряда возможных значений. Будем называть событием тот факт, что в ходе наблюдения случайная величина принимает определенное значение. Когда мы сами создаем условия, чтобы случайная величина приняла какое-то определенное значение, мы производим испытание. Например, мы подбрасываем монету, чтобы узнать, на какую именно сторону в данном испытании она упадет.

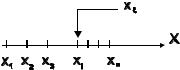
Случайная величина xξ называется дискретной, если она может случайным образом принимать значения только из определенного фиксированного набора

{xi}: x1, x2, …, xn .

Каждому i-му значению из этого набора сопоставляется вероятность того, что случайная величина примет именно это значение: Pi. Эти вероятности нормированы, т.е.

i=1

Нормировка (6.1) означает, что при испытании случайная величина обязательно примет какое-нибудь значение из данного набора.

67

Случайная величина xξ называется непрерывной, если в процессе испытаний она может принимать любое значение из некоторого интервала (a, b).

Любая случайная величина (дискретная, непрерывная) характеризуется функцией распределения F(x), которая равна вероятности того, что при очередном испытании xξ не превзойдет значения x:

Функция распределения является неотрицательной: F(x) ≥ 0 и неубывающей: если x2 > x1, то F(x2) ≥ F(x1). Кроме того, ее значения на бесконечности всегда известны:

Непрерывную случайную величину удобно характеризовать

плотностью вероятности (плотностью распределения) p(x).

Плотность вероятности в точке x равна вероятности того, что

−∞

68

Свойство (6.5а) следует из неотрицательности самой вероятности, а нормировка (6.5б) показывает, что при испытании случайная величина обязательно примет какое-нибудь значение на интервале

(-∞,+∞).

Можно записать функцию плотности вероятности и для дискретной случайной величины

i=1

если воспользоваться дельта-функцией Дирака δ(x - xi). Пример плотности вероятности для непрерывной и дискретной случайных величин приведен на рис.6.1. Изображение дельта-функции на рис. 6.1б условно.

Рис.6.1. Плотности вероятности и функции распределения для непрерывной (а) и дискретной (б) случайных величин

Представим себе испытание, в котором участвуют сразу две случайные величины xξ и yξ. Для описания такого испытания будем использовать совместную плотность вероятности p(x,y), а

распределение одной из случайных величин будем задавать

частичной плотностью вероятности

Для независимых величин совместная плотность вероятности равна произведению их частичных плотностей: p(x, y) = p(x) p( y) .

69

Если в испытании участвуют две случайные величины,

рассматривают их условную плотность вероятности p(x y) . Она

представляет собой плотность вероятности величины xξ при условии, что другая случайная величина примет некоторое конкретное значение: yξ = y. Для условной вероятности существует известная формула Байеса:

В дальнейшем понадобятся следующие два функционала плотности вероятности:

Математическое ожидание (среднее значение) случайной величины:

Среднее значение дискретной случайной величины вычисляется как простая сумма

n

xξ = ∑Pi xi .

i=1

Дисперсия случайной величины xξ:

+∞

Dxξ = M (xξ − xξ )2 = ∫(x − xξ )2 p(x) dx = xξ 2 − xξ 2 .

−∞

Для дисперсии суммы независимых случайных величин справедливо:

D(xξ + yξ ) = Dxξ + Dyξ ,

а для произвольного постоянного множителя α выполняется равенство D(α xξ ) =α 2 Dxξ .

§6.3. Розыгрыш случайной величины

Для решения вычислительных задач методом Монте-Карло нужны наборы значений случайных величин, подчиняющихся различным законам распределения. Получение таких наборов называется случайной выборкой или розыгрышем случайной величины.

70