Metod_adaptivnoy_iskusstvennoy_vyazkosti_1D

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский государственный университет им. Ф.М. Достоевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

+(c2 )in+1

.pdf

Скачиваний:

Добавлен:

12.02.2015

Размер:

325.42 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 2008 год, том 20, номер 8, стр. 48-60

КОНЕЧНО-РАЗНОСТНЫЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ ГАЗОВОЙ ДИНАМИКИ

СВВЕДЕНИЕМ АДАПТИВНОЙ ИСКУССТВЕННОЙ ВЯЗКОСТИ

Институт математического моделирования РАН, Москва

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проекты № 05-07-90230, 06-01-00233).

Предлагается конечно-разностный метод решения уравнений газовой динамики − однородная, монотонная разностная схема второго порядка аппроксимации по времени и пространственной переменной вне областей разрывов и волн сжатия. Рассматривается новый способ введения адаптивной искусственной вязкости (АИВ) в разностную схему. Численно исследуется устойчивость предложенной разностной схемы. Приводятся тестовые расчёты движения контактных разрывов, ударных волн и распада разрывов.

FINITE-DIFFERENCE METHOD FOR COMPUTATION

OF THE GAS DYNAMICS EQUATIONS WITH ARTIFICIAL VISCOSITY

I.V. Popov, I.V. Fryazinov

Institute of Mathematical Modelling of RAS, Moscow

Finite-difference method for computation of the gas dynamics equations with adaptive artificial viscosity (AAV) is proposed. It is homogeneous, monotonous finite-difference scheme of the second order approximation on time and space variables outside of areas of breaks and compression waves. The paper presents new way of introduction of artificial viscosity. It is investigated stability of the scheme. Test calculations of contact breaks movement, shock waves and disintegration of breaks were performed.

Введение

В работе предлагается явная, однородная, практически монотонная разностная схема для одномерных задач газовой динамики на трехточечных шаблонах, слабо размывающая контактные разрывы и ударные волны. Предложенная схема имеет аппроксимацию O(τ2+h2) в областях гладкости решения и вне волн сжатия, τ − шаг по времени и h − шаг по пространственной переменной.

В предлагаемой разностной схеме, наряду с поправками Лакса-Вендроффа, вводится монотонизирующая схему искусственная вязкость μ. Искусственная вязкость вводится в областях немонотонности решения, вне контактного разрыва и волн разряжения. Вязкость находится из условий принципа максимума для схем с «замороженными» коэффициентами.

Решение задачи на каждом временном слое вычисляется в два этапа. На первом этапе («предиктор») находится решение сеточных уравнений с μ=0 во всей области решения задачи. На втором этапе («корректор») анализируется решение, полученное на первом этапе, и в областях немонотонности решения в разностную схему вводится дополнительная искусственная вязкость, монотонизирующая решения в этих областях. Тем самым разностная схема адаптируется к решению задачи. В работе приводятся расчёты модельных и известных тестовых задач.

Методам решения газовой динамики посвящено большое число работ. Сошлёмся здесь лишь на основные монографии, посвящённые решению уравнений газовой динамики: в лагранжевых переменных [1], эйлеровых переменных [2,3] и кинетически согласованные схемы [4]. Обзор работ современных «монотонизированных» разностных схем, в которых проводится достаточно сложная коррекция потока (FCT-метод, TVD-схемы, методы ENO и WENO), можно

Конечно-разностный метод решения уравнений газовой динамики…

найти в книгах [5,6]. В [7] приведены расчеты восьми задач-тестов по десяти разностным схемам.

В данной работе сделаны расчеты тестов из [7] по предлагаемой ниже методике. Приведено сравнение этих результатов с результатами методик, представленных в [7] .

1. Постановка задачи

Рассматриваются одномерные уравнения газовой динамики в эйлеровых переменных:

		∂ρ		+	∂	(vρ) = 0,

		∂t			∂x
	∂I	∂t		∂	∂x
	∂I	+		∂	(v I + p) = 0,

	∂t		∂x
	∂t		∂x
	∂E	+		∂	(v(E + p)) = 0,

	∂t		∂x
	∂t		∂x
где ρ − плотность, v − скорость, I=vρ − импульс,							E = e +	ρv	2	− полная энергия, e=ρε − внутрен-
где ρ − плотность, v − скорость, I=vρ − импульс,							E = e +	2		− полная энергия, e=ρε − внутрен-
								2

няя энергия. Эти уравнения решаются в области 0<x<l, t>0. Система уравнений замыкается уравнением состояния идеального газа p=(γ−1)e.

На концах отрезка и в начальный момент времени задаются функции ρ, v и E (или e). На твердой стенке задаются равные нулю потоки плотности, импульса и равенство нулю скорости.

2.Аппроксимация системы уравнений

Висходной области 0<x<l введём, для простоты изложения, равномерную сетку с шагом

h = Nl−1, где N − число точек разбиения. Введём шаг по времени τ, величину которого опре-

делим позже.

Используем разложение

		ρn+1	= ρn +τ	∂ρn	+	τ2 ∂2ρn	+ .
		ρn+1	= ρn +τ	∂t	+	2 ∂t2	+ .
				∂t		2 ∂t2
		Первую производную по времени выразим из уравнения неразрывности, заменяя её на
−	∂	(vρ)n	. Чтобы найти вторую производную по времени, продифференцируем уравнение
−	∂x	(vρ)n
	∂x

неразрывности по времени и используем уравнение для импульса. Получим для третьего сла-

гаемого следующее представление:

∂2

(ρv2

+ p). В итоге имеем следующее дифференциаль-

но-разностное уравнение:

2 ∂x

ρn+1 −ρn

∂

(ρv)n −

τ ∂2

(ρv2 + p)n

= 0.

∂x

2 ∂x2

В полученном уравнении последнее слагаемое есть поправка Лакса-Вендроффа. Пере-

пишем уравнение в потоковой форме

n+1

−ρ

∂(W )n

= 0,

∂x

где W = ρv −

∂

(ρv2 + p)

− поток массы.

2 ∂x

Выведенное уравнение в разностном виде принимает следующий вид:

И.В. Попов, И.В. Фрязинов

(W )n

−(W )n

ρn+1 = ρn

−τ

i−

(W )n

+vn

ρn

+ρn

τ (ρ

+ p

−(ρ v2

+ p )n

где

i+1

−

i+1

i i

Второе слагаемое в правой части − поправку Лакса-Вендроффа − обозначим через

(LW )n

(ρ

+ p

−(ρ v2

+ p )n

i+1 i+1

i+1

i i

По аналогии запишем в потоковой форме уравнения для импульса и энергии.

Имеем

(W )n 1

−(W )n

Iin+1 = Iin −τ

i−

(W )n

1 −(W )n

En+1 = En

−τ

E i

i−

где

+vn 2 ρn

+ρn

+ pn

(W )n

i+1

−(LW )n 1

− поток импульса,

(LW )

(Iv2 )n

−(Iv2 )n

+vn

− pn

+ pn vn

−vn

i+1

+γ

i+1

− поправка Лак-

са-Вендроффа для импульса,

+vn

γ(en

+en ) +

(ρn

+ρn )

)n 1

− поток полной энергии,

i+1

−

(LW

i+1

((E

+ p)v2 )n

−((E + p)v2 )n

− pn

+en

(LW )n

i+1

vn +

ρn +ρn

i+1 i

i+1

γ pn

+ pn

(v2 )n

−(v2 )n

i+1

− поправка Лакса-Вендроффа для полной энер-

гии E = e + ρ2v2 .

Были проведены численные исследования различных аппроксимаций конвективных слагаемых. Приведенная выше аппроксимация оказалась наилучшей.

Поправки Лакса-Вендроффа приводят к аппроксимации O(τ2 ) . Они не достаточны для

монотонности схемы. Необходимо вводить дополнительную диссипацию в разностную схему (искусственную вязкость).

3. Искусственная вязкость

Введём искусственную вязкость μ в рассматриваемые сеточные уравнения. К потокам (Wq )in+12 добавим слагаемое

	)n			= −μn		qn	−qn
(W		1			1	i+1	i	, где q = ρ, I, E.

μq	i+		2	i+	2		h

Конечно-разностный метод решения уравнений газовой динамики…

Рассмотрим поправку Лакса-Вендроффа для сеточного уравнения неразрывности и выделим из нее диссипативную часть. Поправку Лакса-Вендроффа перепишем в алгебраически эквивалентном виде

(LW )n

τ (ρ

+ p

)n −(ρ v2

+ p )n

i+1

i i

(v2 )n

+(v2 )n

ρn

−ρn

2 )n

−(v2 )n

ρn

+ρn

i+1

ρn

−ρn

S n

−S n

i+1

i +

i+1

Δρ

i+1

S ρ i+1

где S − энтропия;

(ρ

, S

i+1

) + pn (ρ

, S

)

pn (ρ

, S

i+1

) + pn (ρ

, S

)

(ρn

−ρn ) ,

−

Δρ S i+

i+1

(ρ

, S

) + pn (ρ

, S

)

pn (ρ

, S

) + pn (ρ

, S

)

i+1

−

(S n

−S n ) .

i+1

S ρ i+

− сеточный аналог квадрата скорости звука. Обозначим его че-

Слагаемое

Δρ

i+1

рез

)i+1

. Слагаемое

обозначим через αi+1

чим

Окончательно для поправки Лакса-Вендроффа, учитывая введенные обозначения, полу-

(v2 )n

+(v

2 )n

ρn

−ρn

(v2 )n

−(v

2 )n ρn

+ρn

−Sn

. (1)

(LW )n

i+1

+(c2 )n

i+1

+αn

i+1

i+12

В разностной схеме зафиксируем («заморозим») коэффициенты при разностных отноше-

ниях. Разностную схему для уравнения неразрывности запишем в виде

ρn+1

= Aρn

+(1− B)ρn +Cρn

+τF n ,

(2)

i+1

i−1

где

A =

μ+

−

τv

C =

μ+

τv

B = A +C

)

и F n =

(v2 )n

−2(v2 )n +

(v2 )n

−

2S n + S n

i+1

i−1

+α

i+1

i−1

Найдём значение искусственной вязкости μ, при которой разностная схема (2) удовлетворяла бы принципу максимума. Принцип максимума имеет место при A>0, C>0 и B<1. Из этих неравенств следуют ограничения на μ:

−

(v2 +c2 ) ≤ μ ≤

−

(v2

+c2 ) .

(3)

2 2

2τ

И.В. Попов, И.В. Фрязинов

Положительность вязкости μ будет иметь место при

+c2

<1 .

(4)

Оценке (3) удовлетворяют следующие выражения для вязкости μ:

а) μ =

−

;

(5а)

б) μ =

1−

;

(5б)

в) μ =

max

(

,c) 1

−

v2 +c2 k

(5в)

где k=1,2.

Расчеты модельных задач показали, что наилучший результат достигается при выборе вязкости по формуле (5б) при k=2, но меньшая вязкость достигается, если использовать формулу (5в) также при k=2.

В индексной форме вязкость (5б) принимает следующий вид:

						h	v2			+c2								τ		v2 1		+c2 1			2
	μ 1			=					1					1		1	−										,
	μ 1			=		2			1					1	2	1	−	h			2			2			,
			i+	2		2	i+			2		i+			2			h		i+	2	i+		2
			i+				i+					i+								i+		i+

где vn					vn	+vn				cn						cn	+cn			и cn				p
	1		=		i+1		i	,			1		=			i+1			i			= γ			i	.
	1	2	=					,			1	2	=									= γ				.
i+		2				2				i+		2					2			i			ρi
						2											2						ρi

Выражения (5а) и (5в) записываются аналогично. Конечно, предложенная монотонизация является лишь приближенной.

Условие (4) будет иметь место при выполнении неравенства

τ	max	(v2 )n	1		+(c2 )n	1	<1.
				2
h 1≤i≤N		i+			i+		2

Приравняем левую часть последнего неравенства задаваемому числу Куранта, меньшему единицы. Получим

Ku =	τ	max	(v2 )n	1		+(c2 )n	1	<1 .
					2
	h 1≤i≤N		i+			i+		2

Из этого равенства определим шаг по времени τ, который будет переменным

Повторяя проведенные выше рассуждения, для уравнений импульса и энергии вместо условия (4) для идеального газа (γ=5/3 и γ=7/5) получим приближенную оценку:

( 2 ÷ 3)	τ	v2 +c2 <1.	(6)
	h

Отсюда следует, что число Куранта будет ограничено сверху: Ku<0.57÷0.61.

Конечно-разностный метод решения уравнений газовой динамики…

Ограничение числа Куранта определяется уравнениями импульса и энергии, а максимальная искусственная вязкость возникает в уравнении неразрывности. В качестве единой искусственной вязкости для всех уравнений выберем вязкость, полученную для уравнения неразрывности. При постоянных и равных граничных и начальных значениях скорости v=v0 и внутренней энергии e=e0 система уравнений газовой динамики вырождается. Уравнения движения и энергии могут быть получены из уравнения неразрывности умножением соответственно на v0 и

v02 / 2 . Это справедливо и для сеточной задачи при одной и той же вязкости во всех разностных

уравнениях.

Искусственную вязкость будем вводить не на всех сеточных интервалах xi+12 = xi+1 − xi . На части интервалов будем полагать μi+12 = 0 .

4. Области введения искусственной вязкости

Вязкость, содержащаяся в поправках Лакса-Вендроффа, приводит к размыванию контактных разрывов (КР) и ударных волн (УВ). Чтобы не увеличить размывание области КР, в этой области искусственную вязкость вводить не будем.

В области КР величина

∂p		ρ	∂ε	+ε	∂ρ
∂x	= (γ−1)	ρ	∂x	+ε
∂x			∂x		∂x

мала по сравнению с производными

∂ε

∂ρ

. Поэтому величины

∂ε

∂ρ

имеют противопо-

∂x

ложные знаки. Таким образом, в области КР

∂ e

∂ρ

∂x

< 0 .

(КР)

∂x

В области волны разряжения (ВР) также не будем вводить искусственную вязкость, чтобы не понижать точности численного решения. В области ВР справедливо неравенство [2]

∂v	> 0 .	(ВР)
∂x

На «размытой» ударной волне (УВ) выполнено условие [2]

∂∂vx < 0 . (УВ)

Условия

v ∂ρ < 0	(УВ+ВР)
∂x
выполняются на УВ и ВР.
Определим области − интервалы	xi+12 , на которых вводится искусственная вязкость.

Вязкость вводится на интервалах, удовлетворяющих одновременно следующим двум условиям, определяемым по функции плотности:

∂ e

∂ρ > 0, в разностном виде

ei+1

−

(ρ

−ρ ) h2

> 0 ;

i+1

∂x

ρi+1

ρi

2) выполняется одно из неравенств:

∂v

< 0

или

∂ρ

> 0 ,

∂x

54	И.В. Попов, И.В. Фрязинов

в разностном виде (vi+1 −vi )h < 0 или vi+12+vi ρi+1h−ρi > 0.

Первое неравенство означает, что интервал не принадлежит области КР. Условие 2) означает, что интервал не принадлежит области ВР. Первое условие 2) означает, что интервал принадлежит волнам сжатия и УВ.

Искусственная вязкость также вводится в окрестности точек немонотонности решения − локальных экстремумов плотности, соответствующих выполнению неравенства

3) (ρi+1 −ρi )(ρi −ρi−1 )< 0 .

При выполнении последнего неравенства искусственная вязкость вводится на интервалах, примыкающих к узлу xi. На остальных интервалах xi+12 положим μi+12 = 0 .

Таким образом, искусственная вязкость вводится на УВ, в областях осцилляции сеточного решения и не вводится на ВР и КР.

Искусственная вязкость вычисляется по значению решения, полученного на предыдущем временном слое, а выполнение условий 1) и 2) или 3) проверяется по значению решения, полученного на этапе «предиктора» (см. ниже).

Рассматривались также варианты определения областей КР, УВ и ВР по функции ε и ее производной. Однако приведенных выше неравенств оказалось достаточно, чтобы выделить указанные области.

5. Этапы решения задачи

На первом этапе («предиктор») находим все функции в отсутствие искусственной вязкости μ≡0

qn+1 = qn −		τn (W )n			1		−(W )n 1		, q = ρ, I, E, q	= ρ, I , E.
i	i		q	i+			q i−
		h				2		2

Таким образом, находятся все «предикторные» величины.

На втором этапе («корректор») по полученным «предикторным» величинам ρ, I и E определяются интервалы xi+12 , на которых следует ввести искусственную вязкость. Опреде-

ление области, в которой вводится искусственная вязкость, описана в пункте 4 (условия 1 и 2 или 3), а величина вязкости − в пункте 3 (формула 5б).

Для «корректора» имеем следующую разностную схему:

qn+1 = qn+1 −		τn	(W )n			1		−(W )n 1		, q = ρ, I, E.

i	i			μq	i+			μq i−
		h					2		2

Шаг по времени определяется из условия

При сложении уравнений «предиктора» и «корректора» все «предикторные» величины исчезают. Они определяют лишь область введения искусственной вязкости. Как показали численные расчёты, число Куранта не превышает 0.6. Наилучшая точность достигается при стремлении числа Куранта к максимальному значению.

«Предикторное» решение на слое tn+1, найденное при μ≡0, дает слабо осциллирующее решение, что позволяет аккуратно определить области КР, УВ и ВР. «Корректорный» этап решения позволят подавить возникшие осцилляции. Решения, полученные на этапах «предикто-

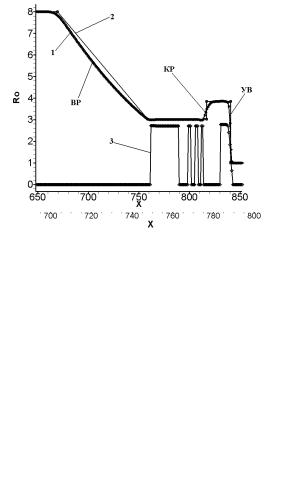
Конечно-разностный метод решения уравнений газовой динамики…

ра» и «корректора», близки, однако отказаться от «корректора» нельзя. Это связано с тем, что при отказе от этапа «коррекции» осцилляции возникают вновь.

6. Численные результаты

Первой задачей, которая была рассмотрена, была задача о движении контактного разрыва. Эта задача решалась при постоянных и равных начальных и граничных значениях скорости v=v0 и внутренней энергии e=e0.

Контактный разрыв размывался не более чем на 7÷8 пространственных интервалов, при прохождении 50 пространственных интервалов и на 8÷10 интервалов при прохождении 150 пространственных интервалов. Расчёты велись при следующих параметрах: v0=1, e0=0.25, h=1, Ku=0.35, γ=7/5, при перепаде плотностей 4 раза.

Во втором расчёте рассматривалась ударная волна. Число интервалов, на которые она размывалась, не превосходило 3÷5 и не зависело от времени. Также в этой постановке рассматривалась задача об отражении ударной волны от твёрдой стенки.

Третьей модельной задачей была задача о распаде сильного разрыва при больших перепадах плотности и давления: для плотности − в 8 раз, а для давления − в 480 раз. Это приводило к образованию сильной ударной волны. Результаты расчёта приведены на рис. 1-5.

Рис.1. Распределение плотности для сильного распада разрыва на момент времени t=4 (1 − сеточное решение, 2 − отрезки, соединяющие границы областей УВ, КР и ВР автомодельного решения, 3 − искусственная вязкость).

Рис.2. Распределение плотности для сильного распада разрыва на момент времени t=8 (1 − сеточное решение, 2 − отрезки, соединяющие границы областей УВ, КР и ВР автомодельного решения, 3 – искусственная вязкость).

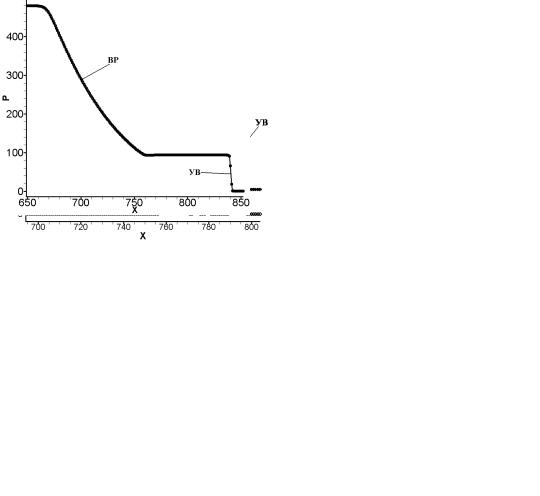
56	И.В. Попов, И.В. Фрязинов

Рис.3. Распределение внутренней энергии	Рис.4. Распределение скорости для сильного
для сильного распада разрыва на момент времени t=8.	распада разрыва на момент времени t=8.

Рис.5. Распределение давления для сильного распада разрыва на момент времени t=8.

Расчёты проводились при следующих параметрах: γ=5/3, на левой границе области ρL=8, vL=0, pL=480, на правой границе области ρR=1, vR=0, pR=1. Начальное положение разрыва находилось в середине отрезка xL=0<x=750<xR=1500. Шаг сетки по пространственной переменной h=1. Число Куранта Ku=0.3.

Четвертой модельной задачей была задача о распаде слабого разрыва, при перепадах плотности и давления: для плотности и давления в 10 раз. Это приводило к образованию слабой ударной волны. Результаты расчёта приведены на рис.6.

Расчёты проводились при следующих параметрах: γ=5/3, на левой границе области ρL=1, vL=0, pL=1, на правой границе области ρR=0.1, vR=0, pR=0.1. Начальное положение разрыва находилось в середине отрезка xL=0<x=750<xR=1500. Шаг сетки по пространственной переменной h=1. Число Куранта Ku=0.3.

Во всех задачах искусственная вязкость определялась по формуле (5б) при k=2.

В процессе численного моделирования по изложенной методике были проведены численные исследования сходимости решения сеточной задачи к решению дифференциальной задачи, имеющей автомодельное решение (распад разрыва). Решение проводилось на последовательности сеток с h=1, h=0.5 и h=0.25. Результаты численных расчетов приведены на рис.7 и 8. Из приведенных расчетных данных следует, что при измельчении сетки происходит уменьшение размывания УВ и КР, видна сходимость численного решения к точному.

Конечно-разностный метод решения уравнений газовой динамики…

Рис 6. Распределение плотности для слабого распада разрыва на момент времени t=286 (1 − сеточное решение, 2 − отрезки, соединяющие границы областей УВ, КР и ВР автомодельного решения).

Рис.7. Расчет сильного распада разрыва для сеток с шагами по пространству h=1, h=0.5

и h=0.25.

Рис.8. Увеличенная зона в области ударной волны и контактного разрыва для расчета, приведенного на рис.7 .

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.11.201882.94 Кб10Metodichka po kursovoi.doc
#
12.02.2015461.93 Кб16Metodichka_1_semestr.pdf
#
23.11.2019151.55 Кб3Metodichka_dlya_kursovykh_rabot_S_V_Checheleva.doc
#
12.02.201566.3 Кб36Metodichka_po_RYa_i_KR(1).docx
#
18.11.201970.14 Кб6Metodologia_doklad.doc
#
12.02.2015325.42 Кб14Metod_adaptivnoy_iskusstvennoy_vyazkosti_1D.pdf
#
11.03.20161.36 Mб8Microelectronic devices on to basis of acoustic waves омгу.pdf
#
12.02.20151.34 Mб103microscopes_technica_osnovy.pdf
#
12.02.201543.01 Кб13money.doc
#
12.02.2015166.4 Кб15Moshina_ostrov_rikotu_1.doc
#
12.02.20151.91 Mб10Mukharovsky_Vvedenie_v_ET.pdf