
- •1) Определение определителя. Док-во
- •6) Вычисление обратной матрицы с помощью присоединенной.
- •7) Правило Крамера.
- •8) Определитель произведения матриц.
- •9) Связь обратимости и неособости.
- •10) Минор порядка k, Количество миноров порядка k. Минорный ранг матрицы. Ранговый минор.
- •11) Вторая теорема о ранге матрицы.
- •12) Метод окаймляющих миноров для вычисления ранга матрицы.
- •13) Понятие комплексного числа в алгебраической форме, его вещественная и мнимая часть.
- •14) Понятие комплексного числа в матричной форме, его вещественная и мнимая часть.
- •15) Понятие комплексного числа в тригонометрической форме, его вещественная и мнимая часть.
- •16) Модуль и аргумент комплексного числа.
- •17) Геометрическое представление комплексных чисел.
- •24) Группа корней степени n из единицы. Сумма всех корней из единицы степени n.
- •44) Задача отделения корней многочлена.
- •45) Примитивные многочлены.
- •47) Признак Эйзенштейна.
14) Понятие комплексного числа в матричной форме, его вещественная и мнимая часть.
Комплексные числа можно также определить как семейство вещественных матриц вида
![]()
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
![]()
мнимой единице —
![]()
15) Понятие комплексного числа в тригонометрической форме, его вещественная и мнимая часть.
Если
вещественную x и мнимую y части
комплексного числа выразить через
модуль ![]() и
аргумент
и
аргумент![]() (
(![]() ,
,![]() ),
то всякое комплексное число
),
то всякое комплексное число![]() ,
кроме нуля, можно записать в тригонометрической
форме
,
кроме нуля, можно записать в тригонометрической
форме
![]()
16) Модуль и аргумент комплексного числа.
Модулем комплексного числа z ϵ C называется неотрицательное действительное число
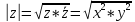 равное
арифметическому квадратному корню из
неотрицательного действительного числа
равное
арифметическому квадратному корню из
неотрицательного действительного числа
 .
.
Очевидно, модуль комплексного числа z равен длине r вектора z.
Аргументом ненулевого комплексного числа z ϵ C называется (любой) угол от положительного направления действительной оси до вектора z. Множество всех таких углов обозначается Arg z.
Главным значением аргумента комплексного числа z ϵ C называется то из значений аргумента, которое принадлежит промежутку (-π;π]. Главное значение аргумента обозначается arg z.
(Аргумент числа 0 не определяется.)
17) Геометрическое представление комплексных чисел.
Двумерный
вектор z = (x; y) = x + y*i изображается как
радиус-вектор с началом в начале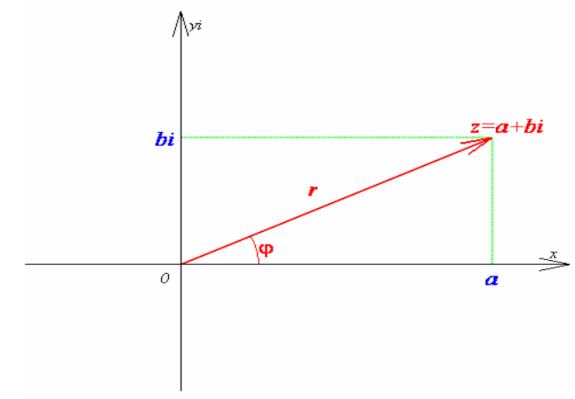
координат
Это и есть "геометрическое представление" комплексного числа.
Две координатные оси плоскости C получают специальные названия: ось, на которой располагаются все действительные числа [векторы x = (x,0)], называется действительной осью, а ось, на которой располагаются чисто мнимые числа [векторы y*i = (0,y )],— мнимой осью.
18) Умножение, сложение, деление комплексных чисел в тригонометрической форме.
Произведение
![]()
Частное

Сложение
19) Умножение, сложение, деление комплексных чисел в алгебраической форме.
Сложение
![]()
Вычитание
![]()
Умножение
![]()
Деление
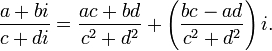
20) Умножение, сложение, деление комплексных чисел в показательной форме комплексного числа.
21) Сопряженное комплексное число.
Два комплексных числа a + b·i и a - b·i называются сопряженными. Сопряженные комплексные числа в сумме дают действительное число 2a.
22) Возведение комплексного числа в степень.
23) Корень степени n из комплексного числа.
В случае же, если z
∈
C – комплексное
число, то для любого натурального числа
n выражение ![]() всегда
имеетсмысли
обозначает все множествокорнейn-й
степени из комплексного числа z.
всегда
имеетсмысли
обозначает все множествокорнейn-й
степени из комплексного числа z.
Обозначение: ![]() ,
где
,
где![]() –
все nкорнейn-й
степени из комплексного числа z, так что
по определению
–
все nкорнейn-й
степени из комплексного числа z, так что
по определению![]()
![]() .
.
В частности,
при n=2 существуют ровно два корня
из комплексного числа z и легко видеть,
что, если ![]() –квадратныйкорень
из комплексного числа z, то
–квадратныйкорень
из комплексного числа z, то![]() ,
т.е. оба корня
,
т.е. оба корня![]() и
и![]() являются
противоположнымикомплекснымичислами,
поэтому вместозаписи
являются
противоположнымикомплекснымичислами,
поэтому вместозаписи![]() применяютзапись
применяютзапись![]() .
.
24) Группа корней степени n из единицы. Сумма всех корней из единицы степени n.
Применяя предложение 32.3 к комплексному числу w = 1, мы сразу получаем, что существует ровно n различных решений уравнения zn= 1 (n значений корня n-й степени из 1):Все zk располагаются на единичной окружности, в вершинах правильного n-угольника.
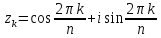 k
= 0,..,n-1
k
= 0,..,n-1
Главным значением корня n-й степени из 1 является z0= 1
25) Многочлен над полем. Степень, коэффициенты многочлена. Равные многочлены. Сумма, произведение многочленов.
Многочленом (или полиномом) степени n над полем P; от переменной x; называется выражение вида f(x) = f0 + f1x + f2x2+ …+ fnxn
Два многочлена f (x) и g(x) (над одним и тем же полем P и от одной и той же переменной x) называются равными (это обозначается f (x) = g(x) или короче f = g), если
1) их степени одинаковы;
2) все соответствующие коэффициенты равны
26) Деление с остатком. Остаток, неполное частное, их степени.
Пусть P — поле. f (x), g (x) — два многочлена с коэффициентами из P [f (x) 6 = 0], тогда существуют (однозначно определенные) многочлены q(x), h(x) из P [x], такие, что g(x) = f (x)q(x) + h(x).
27) Наибольший общий делитель.
Пусть K — целостное кольцо; a ,b ∈ K.
Пусть элемент d является общим делителем элементов a и b, таким, что для него существует линейное представление (с коэффициентами из K) через данные элементы a и b:
d = au + bv; u, v ∈ K
Тогда d ∈ НОД(a,b):
28) Значения многочлена и корни. Теорема Безу.
Корнем многочлена f (x) ∈ P [x] называется корень соответствующей полиномиальной функции
f : P -> P; т. е. такой элемент c ∈ P, что значение f(c) = 0:
1. Остаток от деления многочлена
f (x) положительной степени n над полем P на многочлен первой степени (двучлен) x - c, где c ∈ P , равен значению f (c) многочлена f (x) в точке c.
2. Элемент c является корнем многочлена f (x) тогда и только тогда, когда двучлен x - c делит данный многочлен: x - c | f (x)
29) Разложимые и неприводимые многочлены над полем.
Всякий многочлен (36.18) положительной степени n над алгебраически замкнутым полем P имеет n корней (с учетом их кратностей) и разлагается в произведение n линейных сомножителей:
![]() ,
где c1, c2, .. , cs
— все его (попарно различные) корни;
,
где c1, c2, .. , cs
— все его (попарно различные) корни;
m1, m2, .. , ms— кратности этих корней; m1+ m2 + .. + ms = n.
30) Основная теорема алгебры.
Всякий многочлен
![]() положительной
степени (n > 0) с комплексными коэффициентами
(ak
∈
C; k = 0,…, n; a0≠0
имеет хотя бы один комплексный корень,
положительной
степени (n > 0) с комплексными коэффициентами
(ak
∈
C; k = 0,…, n; a0≠0
имеет хотя бы один комплексный корень,
т. е. всегда найдется такое число z0 ∈ C, что f(z0) = 0)
31) Схема Горнера.
Так называемая схема Горнера является алгоритмом, в значительной степени упрощающим вычисление значений многочлена. Этот алгоритм основан на первом утверждении теоремы Безу [f(x)=(x-c)q(x)+f(c), согласно которой f (c) есть остаток от деления многочлена f (x) на двучлен x-c].
32) Определение простого и кратного корня.
Если у многочлена есть 2 одинаковых корня, то можно сказать, что это корень кратности 2. Если 3 одинаковых корня, то корень кратности 3 и т.д. Кратность корня не может превышать степень многочлена. Корни кратности 1 называются простыми или однократными корнями.
33) Утверждение о комплексном корне многочлена с вещественными коэффициентами.
34) Алгоритм отыскания всех рациональных корней многочлена с целыми коэффициентами.
Задача отыскания рациональных корней для многочлена (42.6), с целыми коэффициентами и ненулевым свободным членом, сводится к задаче перебора всех дробей c=s/t, таких, что s∈S и t∈T где введены обозначения:
S — множество всех делителей свободного члена an
T — множество всех положительных делителей старшего коэффициента a0
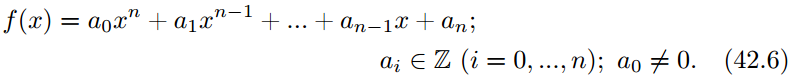 35)
Элементарные симметрические многочлены.
35)
Элементарные симметрические многочлены.
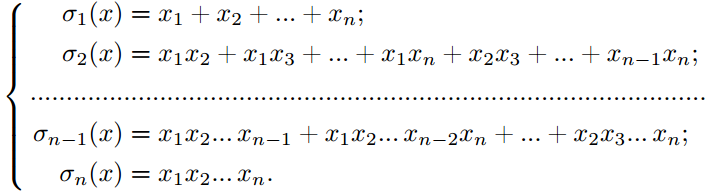
Многочлен
![]() является
суммой всех
является
суммой всех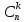 возможных произведений по k (из общего
числа n) переменных. Симметричность и
однородность этих многочленов очевидны,
как и то, что в формулах (49.4) они представлены
в лексикографическом порядке.
возможных произведений по k (из общего
числа n) переменных. Симметричность и
однородность этих многочленов очевидны,
как и то, что в формулах (49.4) они представлены
в лексикографическом порядке.
36) Формулы Виета.

Формулы Виета позволяют однозначно (с точностью до пропорциональности) восстановить многочлен по его корням (в случае, когда их количество равно степени многочлена). Нормализованный многочлен восстанавливается однозначно: a0 = 1; ak= (-1)kσk (k = 1,.., n)
37) Многочлены от n переменных. Лексикографическое упорядочение.
38) Теорема о симметрических многочленах.

39) Интерполяционный многочлен (в форме Лагранжа, метод Ньютона).


40) Производные многочленов.
41) Кратные корни и производные многочленов.

42) Система Штурма.
Ряд Штурма (система Штурма) для вещественного многочлена — последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма.
43) Теорема Штурма.
Пусть ![]() —
ненулевой многочлен с вещественными
коэффициентами,
—
ненулевой многочлен с вещественными
коэффициентами,![]() —
некоторый ряд Штурма для него, [a, b] —
промежуток вещественной прямой, причём
—
некоторый ряд Штурма для него, [a, b] —
промежуток вещественной прямой, причём![]() .
Тогда числоразличных корней
многочлена
.
Тогда числоразличных корней
многочлена ![]() на
промежутке
на
промежутке![]() равно
равно![]() ,
где
,
где![]() —
значение ряда Штурма в точке
—
значение ряда Штурма в точке![]() .
.
Ряд
Штурма существует для любого ненулевого
вещественного многочлена.
Пусть
многочлен ![]() ,
отличающийся от константы, не имеет
кратных корней. Тогда ряд Штурма для
него можно построить, например, следующим
образом:
,
отличающийся от константы, не имеет
кратных корней. Тогда ряд Штурма для
него можно построить, например, следующим
образом:
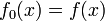 ;
;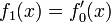 ;
;Если
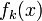 (
(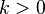 )
имеет корни, то
)
имеет корни, то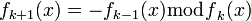 ,
где
,
где —
остаток от деления многочлена
—
остаток от деления многочлена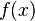 на
многочлен
на
многочлен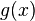 вкольце
многочленов
вкольце
многочленов  ,
иначе
,
иначе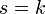 .
.
Для произвольного многочлена, отличающегося от константы, можно положить
![]() ,
,
и далее
следовать приведенному выше способу.
Здесь ![]() —наибольший
общий делитель многочленов
—наибольший
общий делитель многочленов ![]() и
и![]() .
Если многочлен
.
Если многочлен![]() есть
ненулевая константа, то его ряд Штурма
состоит из единственного многочлена
есть
ненулевая константа, то его ряд Штурма
состоит из единственного многочлена![]() .
.
