
Linear00
.pdf
ЛИНЕЙНАЯ АЛГЕБРА
Николай Гордеев
Введение.
Системы линейных уравнений. Метод Гаусса
Карл Фридрих Гаусс |
|
|
|
||||
1777 - 1855. |
|
|
|
|
|
|
|
Карл Фридрих Гаусс - один из |
|||||||
величайших математиков всех времен. |
|||||||
Работы |
Гаусса |
оказали |
огромное |
||||
влияние на развитие алгебры, теории |
|||||||
чисел, |
теории |
функций, |
|
физики, |
|||
астрономии и |
геодезии. С |
1807 |
ãîäà |
||||
и до самой кончины Гаусс руководил |
|||||||
кафедрой |
математики |
и астрономии |
|||||
Г¼ттингенского |
университета, |
à |
|||||
также был директором Г¼ттингенской |
|||||||
обсерватории. |
 |
1824 |
ã. |
Гаусс |
|||
был избран |
иностранным |
|
членом |
||||
Петербургской |
|
(Императорской) |
|||||
академии наук. В 62 года он выучил |
|||||||
русский |
ÿçûê |
è |
â |
своих |
|
письмах |
|
в Петербургскую |
академию |
просил |
|||||
прислать |
åìó |
|
"Капитанскую |
||||
дочку"А.С. Пушкина. |
|
|
|
|
|
|
|
Метод Гаусса алгоритм решения систем линейных уравнений, названный в честь К.Ф. Гаусса. Однако, этот метод был известен в Китае ещ¼ в середине II века до нашей эры. Изложен в древнекитайском трактате "Математика в девяти книгах".
Cистемы линейных уравнений.
1
Определение |
|
0.1. Системой m |
линейных уравнений от n переменных |
|||||||||
(неизвестных, букв) над полем K называется выражение (предикат) вида: |
||||||||||||
|
|
|
|
|
|
a11x1 + a12x2 + + a1nxn = b1 |
|
|
||||
|
|
|
|
|
8 a21x1 + a22x2 + ¢ ¢ ¢ |
+ a2nxn = b2 |
|
|
||||
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
¢ ¢ ¢ |
|
|
|
|
|
|
|
|
|
|
> |
: : : : : : : : : |
|
|
|
; |
(0:1) |
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
ãäå |
aij; bi |
2 K |
. Ïðè |
> |
|
aij |
ïîëÿ |
K |
|
|
|
|
|
|
|
: |
|
|
|
|
|
||||
|
|
|
|
|
> am1x1 + am2x2 + ¢ ¢ ¢ + amnxn = bm |
|
|
|||||
|
|
|
|
|
этом элементы |
|
|
|
называются коэффициентами |
|||
системы |
(0.1), |
à bi |
|
свободными |
членами. (Система линейных |
уравнений, |
||||||
в которой все свободные члены нули, называется однородной. Система линейных уравнений, у которой все коэффициенты и свободные члены нули,
называется нулевой.) Символы xi называются переменными (неизвестными,
буквами) системы (0.1). Решением системы (0.1) называется последовательность элементов ®1; : : : ; ®n ïîëÿ K такая, что:
|
a11®1 + a12®2 + + a1n®n = b1 |
|
|||
8 a21®1 + a22®2 |
+ |
¢ ¢ ¢ |
+ a2n®n = b2 |
: |
|
> |
: : : : : : : : : |
|
¢ ¢ ¢ |
|
|
> |
|
|
|
|
|
> |
|
|
|
|
|
< |
|
|
|
|
|
>
>
>
: am1®1 + am2®2 + ¢ ¢ ¢ + amn®n = bm
Мы можем и мы будем будем рассматривать решения систем линейных уравнений от n переменных как элементы множества
n def
K = K £ K £ ¢ ¢ ¢ £ K = f(®1; : : : ; ®n) j ®i 2 Kg:
Определение 0.2. Система линейных уравнений называется разрешимой, если множество е¼ решений непусто.
Подсистемой системы (0.1) будем называть любую систему линейных уравнений, составленную из некоторых уравнений системы (0.1).
Предложение 0.1. Если система линейных уравнений (0.1)- разрешима, то и любая е¼ подсистема также разрешима.
Доказательство. Непосредственно вытекает из определений 0.1, 0.2. |
¤ |
Нашей задачей является ответ на вопрос: разрешима ли данная система линейных уравнений, и, если разрешима, то описать в том или ином виде множество е¼ решений как подмножество множества Kn. В этом параграфе мы приводим простой
и эффективный алгоритм, называемый методом Гаусса, позволяющий ответить на вопрос о разрешимости системы линейных уравнении и получить описание множества решений.
2
Трапециевидные системы линейных уравнений. |
|
|
|
|
|||||||||||||||
Прежде чем решать систему общего вида (0.1) мы рассмотрим класс систем |
|||||||||||||||||||
специального вида, которые заведомо являются разрешимыми. |
|
|
|
||||||||||||||||
Определение 0.3. Система линейных уравнений вида |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
8 |
c |
|
x |
|
+ c12x2 + |
|
|
+ c1nxn = d1 |
|
|
|
||
|
|
|
|
|
|
|
11 |
|
1 |
c22x2 +¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ + c2nxn = d2 |
|
|
|
||||||
|
|
|
|
|
|
> |
|
|
|
|
|
: : : : : : : : : |
|
|
|
|
|
||
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ ¢ |
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
; |
|
(0:2) |
||
ãäå |
|
· |
|
|
|
>ïðè |
|
è |
|
|
6 |
для любого |
|
|
, называется |
||||
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
> |
|
|
|
|
|
|
ckkxk + ¢ ¢ ¢ + cknxn |
= dk |
|
|
|
||
|
k |
|
n; c |
ij |
= |
0 |
|
|
|
i > j c |
ii |
= 0 |
|
i = 1; : : : ; k |
|
|
|||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
||||
трапециевидной (в уравнениях (0.2) мы не писали слагаемых вида cijxj |
= 0xj äëÿ |
||||||||||||||||||
i < j) .
Определение 0.4. Общим решением системы (0.2) называется последовательность k формул вида
|
xi = fi(xk+1; xk+2; : : : ; xn) |
(0:3) |
|||||||||
i = k; k ¡ 1; : : : ; 1, ãäå |
|
|
1 |
|
|
|
|
||||
|
fk(xk+1; xk+2; : : : ; xn) = |
(dk ¡ ckk+1xk+1 ¡ ¢ ¢ ¢ ¡ cknxn); |
|||||||||
|
|
|
|
||||||||
|
ckk |
||||||||||
fk¡1(xk+1; xk+2; : : : ; xn) = |
|
|
|
1 |
|
(dk¡1 |
¡ ck¡1 kfk(xk+1 |
; xk+2; : : : ; xn) |
|||
|
|
|
|||||||||
ck¡1 k¡1 |
|||||||||||
|
¡ck¡1 k+1xk+1 ¡ ¢ ¢ ¢ ¡ ck¡1 nxn); : : : |
|
|||||||||
|
|
|
|
|
|
|
|
|
j=k |
|
|
|
|
|
1 |
|
|
|
|
jX |
|
||
|
fi(xk+1; xk+2; : : : ; xn) = |
|
cii |
(di ¡ ( |
cijfj(xk+1; xk+2; : : : ; xn)) |
||||||
|
|
|
|
|
|
|
|
|
=i+1 |
|
|
|
¡cik+1xk+1 ¡ ¢ ¢ ¢ ¡ cinxn); : : : : |
(0:4) |
|||||||||
Формулы |
(0.3), получающиеся |
последовательным выражением переменных |
|||||||||
xk; : : : ; x1 |
как функций от |
|
переменных |
xk+1; : : : ; xn |
("подъемом снизу- |
||||||
вверх по системе"(0.2)), определяют соотношения между элементами любой последовательности (®1; : : : ; ®n) 2 Kn, являющейся решением x1 = ®1; : : : ; xn = ®n
системы (0.2).
Åñëè k = n, то формулы (0.3) имеют вид xi = fi, ãäå fi элементы поля K,
вычисляемые по правилам (0.4), без членов вида ¡cik+1xk+1 ¡ ¢ ¢ ¢ ¡ cinxn. Â ýòîì
случае система (0.2) имеет единственное решение.
Пусть k < n. Тогда переменные xk+1; : : : ; xn называются свободными. В этом случае любая последовательность ¯1; : : : ; ¯n¡k 2 K определяет решение системы (0.2) :
®1 := f1(¯1; : : : ; ¯n¡k); : : : ; ®k := fk(¯1; : : : ; ¯n¡k); |
|
®k+1 := ¯1; : : : ; ®n := ¯n¡k: |
(0:5) |
3
Это следует из определения построения общего решения (0.4). Кроме того, любое решение системы (0.2) может быть записано в виде (0.5). Если множество свободных переменных не пусто, то множество решений системы (0.2) равномощно множеству Kn¡k. Действительно, любая (n¡k)- последовательность ¯1; : : : ; ¯n¡k 2 K однозначно
определяет решение системы (0.2). Таким образом, если k < n, т.е., если множество
свободных переменных не пусто, множество решений системы (0.2) содержит более одного решения, а если к тому же поле K бесконечно, то множество решений
системы (0.2) также бесконечно. Суммируя, сказанное выше получаем
Предложение 0.2. Трапециевидная система линейных уравнений (0.2) - разрешима. Она имеет единственное решение тогда и только тогда, когда k = n.
Åñëè k < n, то множество е¼ решений имеет вид
f(f1(¯1; : : : ; ¯n¡k); : : : ; fk(¯1; : : : ; ¯n¡k); ¯1; : : : ; ¯n¡k) j (¯1; : : : ; ¯n¡k) 2 Kn¡kg:
В частности, если K бесконечное поле, то и множество решений системы (0.2) при k < n- бесконечно.
Элементарные преобразования систем линейных уравнений.
Определение 0.5. Следующие преобразования систем линейных уравнений называются элементарными:
I. перестановка местами двух уравнений;
II. перестановка местами двух(переменных (например, от системы
2x1 + 3x2 = 7 x1 ¡ x2 = 3
переходим к системе |
( |
3x2 + 2x1 = 7 ); ¡x2 + x1 = 3
III. почленное умножение одного из уравнений на ненулевой элемент поля (например, вместо i-того уравнения в (0.1)
ai1x1 + ai2x2 + ¢ ¢ ¢ + ainxn = bi
записываем уравнение
®ai1x1 + ®ai2x2 + ¢ ¢ ¢ + ®ainxn = ®bi
для некоторого ® 2 K; ® =6 0);
IV. почленное прибавление к i-тому уравнению j-òîãî (i =6 j), умноженного (почленно) на некоторый элемент поля K (т.е. вместо уравнения
4
ai1x1 + ai2x2 + ¢ ¢ ¢ + ainxn = bi
записываем уравнение
(ai1 + ¸aj1)x1 + (ai2 + ¸aj2)x2 + ¢ ¢ ¢ + (ain + ¸ajn)xn = bi
для некоторого ¸ 2 K);
V. вычеркивание и приписывание нулевых уравнений, т.е. уравнений вида
0x1 + 0x2 + ¢ ¢ ¢ + 0xn = 0:
Замечание 0.1. При обозначении переменных в системах (0.1), (0.2) мы использовали естественную нумерацию слева направо. Однако, при перестановке переменных нумерация меняется. Следует сохранять первоначально принятую нумерацию и учитывать е¼ при описании множества решений в Kn. Например,
единственным решением системы
(
3x2 + 2x1 = 7 ¡x2 + x1 = 3
будет x2 := 15 ; x1 := 165 . Множество решений этой системы будем записывать, используя начальный порядок переменных f(165 ; 15 )g ½ K2.
Пусть S1 система линейных уравнений от n переменных над полем K, à S2 система, полученная из S1 одним из элементарных преобразований. Символом
S1 Ã S2
будем обозначать элементарное преобразование, переводящее систему S1 в систему
S2. Если нужно указать, какое именно элементарное преобразование использовано, будем ставить соответствующий номер преобразования:
I |
; S1 |
II |
; : : : |
S1 Ã S2 |
à S2 |
Предложение 0.3. Каждое из элементарных преобразований обратимо, т.е. для любого элементарного преобразования S1 Ã S2 существует элементарное
преобразование S2 Ã S1.
Доказательство. Непосредственно |
вытекает из определения элементарных |
преобразований. |
¤ |
Отметим, что тождественное преобразование также является элементарным; например, преобразование типа III при ® = 1 èëè òèïà IV ïðè ¸ = 0.
5
Определение 0.6. Две системы линейных уравнений от n переменных над полем K называются эквивалентными, если множества их решений совпадают.
Предложение 0.4. Любая последовательность элементарных преобразований переводит систему линейных уравнений в эквивалентную.
Доказательство. Очевидно, что достаточно проверить утверждение только для случая одного элементарного преобразования S1 Ã S2. Из определений 0.1, 0.5
следует, что любое решение системы S1 является также решением системы S2. Поскольку существует элементарное преобразование S2 Ã S1 (предложение 0.3), любое решение системы S2 также будет решением системы S1. Таким образом, множества решений систем S1; S2 совпадают, а значит это эквивалентные системы (определение 0.6). ¤
Теорема 0.1. Любая ненулевая разрешимая система линейных уравнений приводится к трапециевидной системе (с точностью до перенумерации переменных) конечным числом элементарных преобразований. При этом, число уравнений этой трапециевидной системы не превосходит числа уравнений исходной системы.
Доказательство. Пусть (0.1) ненулевая разрешимая система. Тогда существует хотя бы один коэффициент aij 6= 0 (действительно, если все коэффициенты нули,
а система ненулевая, то в системе имеется уравнение 0x1 + 0x2 + ¢ ¢ ¢ + 0xn = bi 6=
0). Элементарными преобразованиями типа I, II можно добиться, чтобы член aijxj
располагался в левом верхнем углу системы. Поэтому можно сразу предполагать, что a11 6= 0.
Далее проведем доказательство нашего утверждения индукцией по m ( = число уравнений). Для m = 1 утверждение очевидно ( одно уравнение это трапециевидная
система). Предположим, что утверждение теоремы истинно для всех ненулевых разрешимых систем, у которых число уравнений меньше, чем m. Рассмотрим систему
(0.1), для которой a11 6= 0. Для любого i > 1 к строке с номером i прибавим первую
строку, умноженную на ¡ai1
a11 . Получим систему
8
> a x
> 11 1
>
<
>
>
>
:
+ a12x2 + ¢ ¢ ¢ + a1nxn = b1 |
|
|||||||||||||
a0 |
x |
2 |
+ |
¢ ¢ ¢ |
+ a0 |
x |
n |
= b0 |
(0:6) |
|||||
22 |
|
|
|
|
|
2n |
|
|
2 |
|||||
: : : : : : : : : |
|
|
|
|
|
|
|
|||||||
a0 |
|
x |
2 |
+ |
¢ ¢ ¢ |
+ a0 |
|
x |
n |
= b0 |
||||
m2 |
|
|
|
|
mn |
|
|
m |
||||||
6

для некоторых a0ij; b0 2 K. Ввиду предложения 0.4, система линейных уравнений (0.6)
также разрешима, а значит и система |
|
|
|
|
(0:7) |
||
|
8 |
:a:220 :x: :2:+: :¢:¢ ¢ + a20 nxn = b20 |
|||||
|
> |
|
|
|
|
|
|
является разрешимой |
: |
|
|
|
|
|
|
|
< |
a0 |
x2 + |
¢ ¢ ¢ |
+ a0 |
xn = b0 |
|
|
> |
m2 |
|
mn |
|
m |
|
|
(предложение 0.1). Если эта система нулевая, то мы вычеркнем |
||||||
все уравнения (0.7) из системы (0.6) и получим одно уравнение, являющееся |
|||||||
трапециевидной системой. Если система (0.7)- ненулевая, то по предположению |
|||||||
индукции она приводится элементарными преобразованиями к трапециевидной |
|||||||
системе. Отметим, что все элементарные преобразования системы (0.7), кроме |
|||||||
типа II, можно рассматривать и как элементарные преобразования системы |
|||||||
(0.6), а преобразование типа II перестановки переменных (с номерами > 1) , |
|||||||
можно производить и в первом уравнении системы (0.6). Таким образом, приведя |
|||||||
элементарными преобразованиями подсистему (0.7) к трапециевидной системе, мы |
|||||||
приведем элементарными преобразованиями и систему (0.6) к трапециевидной |
|||||||
системе. Так как мы не приписывали новых уравнений, то число уравнений |
|||||||
трапециевидной системы · m. |
|
|
|
|
|
¤ |
|
Следствие 0.1. Однородная система уравнений над полем K, у которой число уравнений m меньше числа переменных n имеет ненулевое решение. Если при этом, поле K бесконечно, то множество решений такой системы бесконечно.
Доказательство. Однородная система уравнений разрешима ( (0; : : : ; 0) является
решением такой системы). Ввиду теоремы 0.1 такая система приводится к эквивалентной трапециевидной системе. ¤
Алгоритм Гаусса.
Доказательство теоремы 0.1 содержит алгоритм, позволяющий выяснить разрешимость ненулевой1 системы линейных уравнений (0.1) и в случае е¼ разрешимости найти общее решение системы. А именно, алгоритм состоит из следующих шагов:
Замечание 0.2. В схеме, приведенной выше, Шаги представляют собой набор элементарных действий, порядок выполнения которых, не определ¼н здесь
однозначно. Например, в Шаге 1 поиск коэффициента aij =6 0 можно организовать следующим образом: для фиксированного номера переменной j = 1; : : : ; n, меняя номер уравнения i = 1; : : : ; m, проверяем, является ли нулем соответствующий коэффициент aij.
1множество решений нулевой системы линейных уравнений это вс¼ множество Kn
7
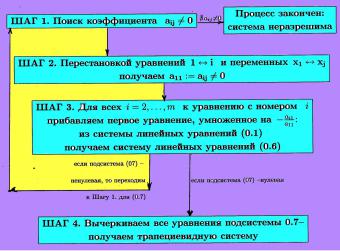
Рис. 1. Алгоритм Гаусса
Замечание 0.3. При переходе от Шага 3 к Шагу 1, т.е. от системы к подсистеме, надо иметь ввиду, что уравнения, которые находятся "выше" уравнений подсистемы, сохраняются и каждая подстановка переменных подсистемы меняет местами и соответствующие переменные в этих уравнениях.
Замечание 0.4. В литературе методом (алгоритмом) Гаусса иногда называют не только приведение системы линейных уравнений к трапециевидной форме, но и вычисление общего решения (0.3) по формулам (0.4). При этом, приведение системы линейных уравнений к трапециевидной форме называют прямым процессом, а вычисление общего решения (0.3) по формулам (0.4) обратным. Ниже под методом (алгоритмом) Гаусса мы будем понимать только приведение системы линейных уравнений к трапециевидной форме методом исключения переменных (Рис.1).
Алгоритм Гаусса дает ответ на вопрос о разрешимости системы (0.1) и позволяет определить с помощью формул множество решений. Действительно, если алгоритм Гаусса приведет систему (0.1) к виду (0.2), то система (0.1) разрешима, и общее решение (0.3) системы (0.2) определяют также решение системы (0.1) (предложение 0.4). Эти формулы будем называть также общим решением исходной системы
(0.1). Так как выбор поиска aij 6= 0 в Шаге 1 неоднозначен, то вид полученной
системы (0.2) также не определяется однозначно, а, значит, неоднозначен и выбор свободных переменных. Однако, число свободных переменных не зависит от выбора, использованных элементарных преобразований (это будет доказано ниже).
Таким образом, возможность приведения системы (0.1) к виду (0.2), используя алгоритм Гаусса, гарантирует разрешимость системы (0.1). Остановка алгоритма Гаусса возможна только в одном случае, оставшиеся уравнения, с которыми нужно
8
проделать очередной шаг алгоритма Гаусса, имеют вид
0x1 + 0x2 + ¢ ¢ ¢ + 0xn = bi
(è bi 6= 0 хотя бы для одного i). Следовательно, для разрешимости системы (0.1)
необходимым и достаточным условием является возможность приведения системы к трапециевидной форме (0.2) методом Гаусса.
|
|
ПРИМЕР. |
Найдем решения системы линейных уравнений над полем Q. |
||
> |
|
3x3 + x4 + 2x5 = 1 |
|
¡ |
|
> |
|
|
> |
|
|
> |
|
|
< |
|
2x2 + 2x3 x4 + 4x5 = 2 |
8 |
|
|
> |
2x1 |
+ 3x3 + x4 + 2x5 = 3 |
> |
|
|
> |
|
|
> |
|
|
> |
|
|
: |
|
+ 2x2 + 8x3 + x4 + 8x5 = 6 |
> 2x1 |
||
Ниже будем обозначать:
(i) ¡ уравнение с номером i; [j] ¡ переменная с номером j: Элементарными преобразованиями приводим систему к трапециевидной форме:
> |
|
|
|
3x3 + x4 + 2x5 = 1 |
|
à |
> |
x4 + |
3x3 |
|
|
+ 2x5 = 1 |
||||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
< |
|
|
2x2 |
+ 2x3 |
|
x4 |
+ 4x5 |
= 2 |
|
|
< |
x4 + 2x2 + 2x3 |
|
+ 4x5 = 2 |
||||||||
8 |
|
|
¡ |
II:([1]$[4]) |
8 |
|
||||||||||||||||
> |
2x1 |
+ 2x2 |
+ 8x3 |
|
+ 8x5 |
= 6 |
> |
¡ |
+ 2x2 + 8x3 |
+ 2x1 |
+ 8x5 |
= 6 |
||||||||||
> |
+ x4 |
|
|
> x4 |
||||||||||||||||||
> |
2x1 |
|
+ 3x3 |
+ x4 |
+ 2x5 |
= 3 |
|
|
> x4 |
+ 3x3 |
+ 2x1 |
+ 2x5 |
= 3 |
|||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
8 4 |
|
|
|
: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2x2 + 5x3 |
+ 6x5 |
= 3 |
|
|
|
|
|
|||||
|
|
|
|
à |
|
|
> |
x |
+ |
3x3 |
|
+ 2x5 |
= 1 |
à |
|
|
|
|||||
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
2x1 |
= 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV :(2)+(1);(3)¡(1);(4)¡(1) |
< |
|
|
|
|
|
|
|
|
IV :(4)¡(2) |
|
|
|||||||
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
2x2 + 5x3 + 2x1 + 6x5 = 5 |
|
|
|
|
|
|||||
8 |
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|||||||
|
2x2 + 5x3 |
|
+ 6x5 |
= 3 |
|
8 |
|
2x2 |
+ 5x3 |
+ 6x5 |
= 3 |
|||||||||||
> |
x4 |
+ |
3x3 |
|
|
+ 2x5 |
= 1 |
à |
> |
x4 |
|
+ 3x3 |
+ 2x5 |
= 1 |
||||||||
> |
|
|
|
|
2x1 |
|
|
= 2 |
|
> |
|
|
2x1 |
|
|
|
= 2 |
|||||
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
II:[3]¡[1] |
< |
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
2x1 |
|
|
= 2 |
> |
|
|
2x1 |
|
|
|
= 2 |
||||||
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|||||||||
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
9
à |
> |
x |
4 |
|
+ 3x3 + 2x5 = 1 |
|
à |
|
|
2x2 |
+ 5x3 + 6x5 = 3 |
|
|||||
|
8 |
|
|
âû÷. |
||||
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
IV :(4)¡(3) |
< |
|
|
|
|
|
V : |
[4] |
> |
|
|
|
2x1 |
= 2 |
|||
|
> |
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
: |
|
|
|
|
0 = 0 |
|
|
|
> |
|
|
|
|
|
|
|
8 |
|
|
2x2 |
|
|
+ 5x3 |
+ 6x5 |
= 3 |
|
получили трапециевидную систему: |
||||
> |
x4 |
|
|
|
|
|
|
+ 3x3 |
+ 2x5 |
= 1 |
¡ |
|
||
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полагаем:> |
x |
; x |
|
- |
2x1 |
|
|
|
= 2 |
|
|
|||
> |
|
5 |
свободные |
переменные. Общее решение системы линейных |
||||||||||
: |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(3 ¡ 5x3 ¡ 6x5); x4 = 1 ¡ 3x3 ¡ 2x5 |
||||
|
|
|
|
|
x1 = 1; x2 = |
|
||||||||
|
|
|
|
|
2 |
|||||||||
Множество решений системы, как подмножество в Q5: |
||||||||||||||
|
|
|
|
|
f(1; |
1 |
(3 ¡ 5® ¡ 6¯); ®; 1 ¡ 3® ¡ 2¯; ¯) j ®; ¯ 2 Qg: |
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
||||||||
Упражнение.
Напишите программу (в пакете Maple или SAGE) для алгоритма Гаусса (Рис 1).
Комментарии
Поле определения системы. При определении системы линейных уравнений над некоторым полем K ìû
должны зафиксировать некоторое поле, содержащее все коэффициенты системы. Выбор такого поля не определяется самими коэффициентами. Например, систему, у которой коэффициенты являются рациональными числами, можно рассматривать как систему над полями Q; R; C и любым другим полем характеристики ноль.
Системы линейных уравнений над кольцом. Можно рассматривать системы линейных уравнений и над кольцами. В этом случае все коэффициенты aij являются элементами некоторого кольца K и все решения системы
мы ищем в множестве Kn. Однако, для колец вопрос о решении систем становится значительно сложнее. Например,
даже вопрос о решении простейшей системы, состоящей из одного уравнения ax + by = c над кольцом целых чисел,
требует некоторых усилий.
Методы решения систем линейных уравнений. Существует множество различных методов решения систем линейных уравнений. Некоторые из них обсуждаются в приведенной ниже литературе. Для систем с небольшим числом уравнений и переменных метод Гаусса является достаточно эффективным. Следует отметить, что в настоящее
время имеются в пакетах программ Maple, SAGE и др. программы, позволяющие находить не только приближенные численные решения, но и точные общие решения систем линейных уравнений.
10
