Лекция №29 Понятие λ-матрицы.

Определение

λ-матрица — квадратная матрица, элементами которой являются многочлены над некоторым числовым полем. Если имеется некоторый элемент матрицы, который является многочленом степени l, и нет элементов матрицы степени большей чем l, то l — степень λ-матрицы.

, (1)

Используя обычные операции над матрицами, любую λ-матрицу можно представить в виде:

(2)

В случае если определитель матрицы отличен от нуля, то λ-матрица называется регулярной.

Пример

(3)

Теорема о приведении λ-матрицы к каноническому виду

Всякая λ-матрица эквивалентна некоторой канонической -матрице, то есть она приводится элементарными преобразованиями к каноническому виду.

Доказательство

Будем доказывать эту теорему методом математической индукции. Действительно, при n=1 будет

(4)

Если , то наша матрица уже каноническая. Если же, то достаточно разделить многочленна его старший коэффициент – это будет элементарное преобразование матрицы – и мы получим каноническую матрицу.

Пусть теорема уже доказана для λ-матриц порядка . Рассмотрим произвольную λ-матрицупорядкаn. Если она нулевая, то уже является канонической. Поэтому будем считать, что среди элементов матрицы имеются ненулевые.

Переставляя строки и столбцы матрицы , можно перевести один из ненулевых элементов в левый верхний угол. Таким образом, среди λ-матриц, эквивалентных матрице, имеются такие, в левом верхнем углу которых стоит ненулевой многочлен. Рассмотрим все такие матрицы. Можно найти среди всех λ-матриц, эквивалентных матрицеи имеющих ненулевой элемент в левом верхнем углу, одну из таких, что многочлен, стоящий в её левом верхнем углу, имеет наименьшую возможную степень. Деля первую строку этой матрицы на старший коэффициент указанного многочлена, мы получим такую λ-матрицу, эквивалентную матрице,

, (5)

что , старший коэффициент этого многочлена равен 1.

Докажем, что все элементы первой строки и первого столбца полученной матрицы нацело делятся на 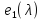. Пусть для

, (6)

где степень меньше степени, еслиотлично от нуля. Тогда, вычитая изj-го столбца матрицы первый столбец, умноженный на , а затем переставляя первый иj-й столбцы, мы придём к матрице, эквивалентной матрице , в левом верхнем углу которой стоит многочлен, то есть многочлен меньшей степени, чем, что противоречит выбору этого многочлена. Отсюда следует, что и требовалось доказать.

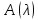Вычитая теперь из j-го столбца первый столбец, умноженный на , заменим элементнулём. Делая такие преобразования дляj=2, 3, … , n, заменим нулями все элементы . Аналогично заменяются нулями все элементыСледовательно, мы придём к такой матрице, эквивалентной матрице, в левом верхнем углу которой стоит многочлен, а все остальные элементы первой строки и первого столбца равны нулю,

(7)

По индуктивному предположению, матрица (n-1)-го порядка, стоящая в правом нижнем углу полученной матрицы (7), элементарными преобразованиями приводится к каноническому виду:

(8)

Совершив эти же преобразования, мы получим, что

(9)

Теорема об эквивалентности двух λ-матриц

Всякая λ-матрица эквивалентна лишь одной канонической матрице.

Доказательство

Пусть дана произвольная λ-матрица А(λ) порядка n. Фиксируем некоторое натуральное число k, ,и рассмотрим все миноры k-го порядка матрицы А(λ). Вычисляя эти миноры, получим конечную систему многочленов от λ; наибольший общий делитель этой системы многочленов, взятый со старшим коэффициентом 1, обозначим через .

Получили многочлены

(10)

однозначно определяемые самой матрицей А(λ). При этом есть наибольший общий делитель всех элементов матрицы А(λ), взятый с коэффициентом 1, а равен определителю матрицы А(λ), делённому на его старший коэффициент. Если матрица А(λ) имеет ранг r, то

, (11)

в то время как все остальные многочлены системы (10) отличны от 0.

Определение

Наибольший общий делитель 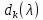всех миноров k-го порядка λ-матрицы А(λ), k=1, 2, …, n, не меняется при выполнении в матрице А(λ) элементарных преобразований.

Пусть к i-ой строке матрицы А(λ) прибавляется её j-я строка, j≠i, умноженная на многочлен φ(λ); получающуюся матрицу обозначим через , а наибольший общий делитель всех её миноров k-го порядка, взятый со старшим коэффициентом 1 – через .

Ясно, что не будут меняться те миноры, через которые i-я строка не проходит. Не меняются и те миноры, через которые проходят как i-я, так и j-я строки, так как определитель не меняется от прибавления к одной его строке кратного другой его строки. Возьмём любой из тех миноров k-го порядка, через которые проходит i-я строка, но не проходит j-я; обозначим его через M. Соответствующий минор матрицы можно представить, как сумму минораМ и умноженного на φ(λ) минора М’ матрицы А(λ), получающегося из минора М заменой элементов i-ой строки матрицы А(λ) соответствующими элементами её j-ой строки. Так как М и М’ делятся на то иМ+ φ(λ)М’ будет делиться на . Отсюда следует, что все миноры матрицынацело делятся на, а поэтому иделится на. Так как для рассматриваемого элементарного преобразования существует обратное того же типа, то иделится на. Если учесть, что старшие коэффициенты обоих многочленов равны 1, то, что и требовалось доказать.