
Понятие линейного оператора
.docxЛекция 28
Понятие линейного оператора
Определение
1. Рассмотрим
два линейных пространства R и R1
над
полем K.
Оператором ã называется любое правило,
согласно которому каждому вектору
 ставится в соответствие единственный
вектор
ставится в соответствие единственный
вектор
 ,
такой, что
,
такой, что
 .
Вектор
.
Вектор
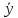 называется образом
вектора
называется образом
вектора
 ,
а вектор
,
а вектор
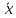 - прообразом
вектора
- прообразом
вектора
 .
.
Определение 2. Оператор ã называется линейным, если выполняются следующие 2 условия:
a)
 ;
;
b)
 .
.
Матрица линейного оператора в заданном базисе
Пусть
 и
и
 – линейные пространства размерности
n
и m
соответственно.
Пусть A
– линейный оператор, действующий из
L1
в
L2.
Зафиксируем в пространстве L1
базис
– линейные пространства размерности
n
и m
соответственно.
Пусть A
– линейный оператор, действующий из
L1
в
L2.
Зафиксируем в пространстве L1
базис
 .
Рассмотрим действие линейного оператора
A
на векторы базиса
.
Рассмотрим действие линейного оператора
A
на векторы базиса
 Разложим векторы
Разложим векторы
 по базису
по базису
 :
:




Коэффициенты
 этих разложений образуют матрицу
этих разложений образуют матрицу
 ,
которая называется матрицей
линейного oператора
A
в паре базисов e
и f.
,
которая называется матрицей
линейного oператора
A
в паре базисов e
и f.
Основные действия над линейными операторами
Пусть L1 и L2 – произвольные линейные пространства.
Определение.
Операторы
 и
и
 называются равными, если
называются равными, если
 .
.
Определение.
Суммой операторов
 и
и
 называется
оператор
называется
оператор
 ,
действующий по правилу
,
действующий по правилу

Определение.
Произведением оператора
 на действительное число λ называется
оператор
на действительное число λ называется
оператор
 ,
действующий по правилу
,
действующий по правилу
 .
.
Определение.
Произведением операторов
 и
и
 называется
оператор
называется
оператор
 ,
действующий по правилу
,
действующий по правилу

Определение.
Пусть
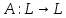 .
Определим степень оператора A следующим
образом:
.
Определим степень оператора A следующим
образом:
 ,
где
,
где
 единичный оператор, действующий по
правилу
единичный оператор, действующий по
правилу
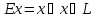 .
.
Легко доказать следующие утверждения.
Утверждение
1.
Если A
и B
– линейные операторы, то
 также линейные операторы (при условии,
что
также линейные операторы (при условии,
что
 существуют).
существуют).
Утверждение 2. В конечномерных линейных пространствах произведению линейного оператора на число, сумме линейных операторов и произведению линейных операторов соответствуют такие же действия с их матрицами.
Понятие собственного вектора и собственного значения линейного оператора. Характеристическая матрица и характеристический многочлен матрицы. Подобные матрицы, их характеристические многочлены
Пусть
 выражается линейно через
выражается линейно через
 :
:
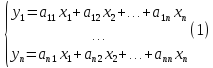 ,
,
тогда
 с координатами
с координатами
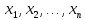 переводятся в вектор
переводятся в вектор
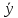 с помощью линейного преобразования (1)
с матрицей А.
с помощью линейного преобразования (1)
с матрицей А.
Пусть
имеется линейное преобразование
(оператор) с матрицей А,
если существует
 ,
такая, что
,
такая, что
 (2), то λ называется собственным числом
(значением), а
(2), то λ называется собственным числом
(значением), а
 - собственным вектором линейного
преобразования соответствующего числа
λ.
- собственным вектором линейного
преобразования соответствующего числа
λ.
Из
(2) следует
 ,
где E
–
единичная матрица.
,
где E
–
единичная матрица.
Матричное уравнение соответствует следующей системе уравнений:

Чтобы
эта система имела ненулевое решение,
необходимо, чтобы ее определитель был
равен 0, поэтому собственные значения
являются корнями уравнения
 ,
то есть
,
то есть

(5) называется характеристическим уравнением.
Чтобы найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей А, поступает следующим образом:
-
составляют характеристическое уравнение (5);
-
находим корни λ характеристического уравнения;
-
каждое
 подставляется в систему (4). Находим все
ее линейно-независимые решения, которые
будут определять собственный вектор,
соответствующий данному
подставляется в систему (4). Находим все
ее линейно-независимые решения, которые
будут определять собственный вектор,
соответствующий данному
 .
Для каждого
.
Для каждого
 существует бесконечно много коллинеарных
соответствующих векторов.
существует бесконечно много коллинеарных
соответствующих векторов.
Определение.
Характеристическим многочленом
 относительно числа λ называется многочлен
вида
относительно числа λ называется многочлен
вида
 .
.
Характеристические многочлены подобных матриц совпадают.
Характеристический многочлен и характеристические корни линейного оператора
Определение.
Уравнение
 называется характеристическим
уравнением оператора
A.
называется характеристическим
уравнением оператора
A.
Теорема. Для того чтобы число λ являлось собственным значением
оператора A, необходимо и достаточно, чтобы оно было действительным корнем характеристического уравнения оператора A.
Теорема о линейной независимости собственных векторов, отвечающих различным собственным значениям линейного оператора.
Теорема.
Пусть собственные значения
 линейного оператора A
попарно различны. Тогда система
соответствующих им собственных векторов
линейного оператора A
попарно различны. Тогда система
соответствующих им собственных векторов
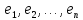 линейно независима.
линейно независима.
Доказательство.
Доказательство опирается на метод математической индукции, проводимый по количеству n векторов в системе. При n = 1 утверждение теоремы верно, так как линейная независимость системы из одного вектора означает, что этот вектор ненулевой, а собственный вектор, согласно определении., является ненулевым.
Пусть
утверждение верно при n
= m,
то есть для произвольной системы из m
собственных векторов
 .
Добавим к системе векторов еще один
собственный вектор
.
Добавим к системе векторов еще один
собственный вектор
 ,
отвечающий собственному значению
,
отвечающий собственному значению
 ,
и докажем, что расширенная таким способом
система векторов останется линейно
независимой. Рассмотрим произвольную
линейную комбинацию полученной системы
собственных векторов и предположим,
что она равна нулевому вектору:
,
и докажем, что расширенная таким способом
система векторов останется линейно
независимой. Рассмотрим произвольную
линейную комбинацию полученной системы
собственных векторов и предположим,
что она равна нулевому вектору:

К равенству (1) применим линейный оператор A и в результате получим еще одно векторное равенство

Учтем,
что векторы
 являются собственными:
являются собственными:
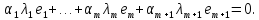
Вспоминая,
что система векторов
 ,
по предположению, линейно независима,
делаем вывод, что у полученной линейной
комбинации все коэффициенты равны нулю:
,
по предположению, линейно независима,
делаем вывод, что у полученной линейной
комбинации все коэффициенты равны нулю:

Поскольку
все собственные значения λi
попарно различны, то из равенств (3)
следует, что
 .
Значит соотношение (1) можно записать в
виде
.
Значит соотношение (1) можно записать в
виде
 ,
а так как вектор
,
а так как вектор
 ненулевой (как собственный вектор), то
ненулевой (как собственный вектор), то
 .
В итоге получаем, что равенство (1)
выполняется лишь в случае, когда все
коэффициенты
.
В итоге получаем, что равенство (1)
выполняется лишь в случае, когда все
коэффициенты
 ,
равны нулю. Тем самым мы доказали, что
система векторов
,
равны нулю. Тем самым мы доказали, что
система векторов
 линейно независима.
линейно независима.
Теорема о существовании базиса, состоящего из собственных векторов линейного оператора
Теорема 1. Матрица линейного оператора A, действующего в линейном пространстве, в данном базисе является диагональной тогда и только тогда, когда все векторы этого базиса являются собственными для оператора A.
Доказательство:
Пусть
A
— матрица линейного оператора A
в базисе
 .
Согласно определению, j-м
столбцом матрицы A
является столбец координат вектора
Abj.
.
Согласно определению, j-м
столбцом матрицы A
является столбец координат вектора
Abj.
Если матрица A является диагональной, то произвольно взятый ее j-й столбец имеет вид (0 . . . 0 µj 0 . . . 0)т (единственный ненулевой элемент стоит на j-м месте). Для вектора Abj получаем представление Abj = b(0 . . . 0 µj 0 . . . 0)т= µjbj, которое как раз и означает, что вектор bj является собственным с собственным значением µj. Значит, все базисные векторы являются собственными, а все диагональные элементы матрицы A являются собственными значениями.
Верно и обратное. Если каждый вектор bj является собственным для линейного оператора A и ему отвечает собственное значение λj, то Abj = λjbj = b(0 . . . 0 λj 0 . . . 0)т, т.е. в матрице оператора A в этом базисе равны нулю все элементы, кроме диагональных, а диагональный элемент в j-м столбце равен λj.
Следствие 1. Если характеристическое уравнение линейного оператора, действующего в n-мерном линейном пространстве, имеет n попарно различных действительных корней, то существует базис, в котором матрица этого оператора является диагональной.
Доказательство:
Каждый действительный корень характеристического уравнения является собственным значением линейного оператора. Каждому из таких корней можно сопоставить хотя бы по одномусобственному вектору. Система выбранных таким образом векторов, согласно теореме о линейной независимости собственных векторов, является линейно независимой, а так как количество n векторов в ней равно размерности линейного пространства, она является базисом. Этот базис состоит из собственных векторов.
Согласно теореме 1, матрица линейного оператора в этом базисе имеет диагональный вид.
Следствие 2. Если характеристическое уравнение квадратной матрицы порядка n имеет n попарно различных действительных корней, то эта матрица подобна некоторой диагональной.
Доказательство:
Пусть характеристическое уравнение матрицы A порядка n имеет n различных действительных корней. Выберем произвольное n-мерное линейное пространство L, зафиксируем в нем некоторый базис b = (b1, b2, . . . , bn) и рассмотрим линейный оператор A, матрицей которого в базисе b является матрица A. По теореме 1 существует базис, в котором матрица A'
этого оператора диагональна. Матрицы A и A' подобны. Отметим, что
на диагонали матрицы A' стоят все попарно различные собственные значения матрицы A.
