
- •0: Определения, способы задания графов. Определения
- •Способы задания графов
- •1: Бинарные отношения. Свойства бинарных отношений. Как их проверять по матрице и графу?
- •7: Гамильтоновы графы. Гамильтоновость и точки сочленения. Теоремы Дирака и Оре. Гамильтоновы графы
- •Гамильтоновость и точки сочленения
- •11: Применения формулы Эйлера: непланарность k5 и k33 Следствие теоремы Эйлера
- •Непланарность k5
- •Непланарность графа k3,3
- •12: Обход в ширину
- •13: Обход в глубину
- •14: Центр, радиус и диаметр графа
- •15: Сильная связность. Граф конденсации. Сильная связность
- •Граф конденсации
- •16: Алгоритм Косарайю
- •17: Раскраски графов. Хроматический многочлен.
- •18: Хроматический многочлен дерева и цикла.
- •19: Сети и потоки. Теорема Форда-Фалкерсона. Алгоритм Форда-Фалкерсона. Алгоритм поиска максимального потока в плоском графе. Сети и потоки
- •20: Двудольные графы. Паросочетания Двудольные графы
- •Паросочетания
- •Алгоритм построения максимального паросочетания двудольного графа
- •21: Остовные деревья. Алгоритм Прима.
- •22: Остовные деревья. Алгоритм Краскала.
- •23: Алгоритм Дейкстры
- •24: Алгоритм Флойда
20: Двудольные графы. Паросочетания Двудольные графы
Двудольный
граф — граф
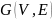 такой, что
— объединение непересекающихся непустых
множеств
и
и каждое ребро соединяет вершину из
с вершиной из
.
такой, что
— объединение непересекающихся непустых
множеств
и
и каждое ребро соединяет вершину из
с вершиной из
.
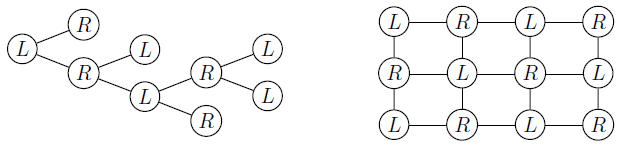
Теорема. Граф двудольный тогда и только тогда, когда в нём нет циклов нечётной длины.
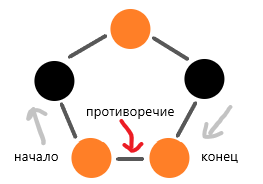 Доказательство.
Пусть
граф имеет цикл нечётной длины.
Первую
вершину цикла занесём в первую долю,
следующую — во вторую и т. д.
Т. к. цикл
нечётной длины, последняя вершина цикла
будет одной доли с первой, что противоречит
определению двудольного графа.
Доказательство.
Пусть
граф имеет цикл нечётной длины.
Первую
вершину цикла занесём в первую долю,
следующую — во вторую и т. д.
Т. к. цикл
нечётной длины, последняя вершина цикла
будет одной доли с первой, что противоречит
определению двудольного графа.
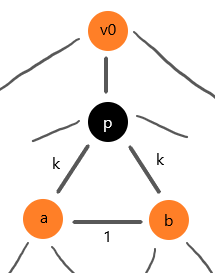 Доказательство
в обратную сторону.
Начнём обход
в ширину, чередуя занесение в ту или
иную долю при увеличении расстояния
Доказательство
в обратную сторону.
Начнём обход
в ширину, чередуя занесение в ту или
иную долю при увеличении расстояния
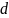 от начальной вершины
от начальной вершины
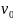 .
Некоторая
вершина
может быть соединена с некоторой вершиной
на расстоянии
.
Если
.
Некоторая
вершина
может быть соединена с некоторой вершиной
на расстоянии
.
Если
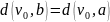 ,
то можно найти общего предка
,
то можно найти общего предка
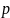 этих вершин, что
этих вершин, что
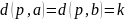 .
Тогда
длина цикла через вершины
.
Тогда
длина цикла через вершины
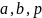 будет равна
будет равна
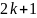 — нечётному числу.
— нечётному числу.
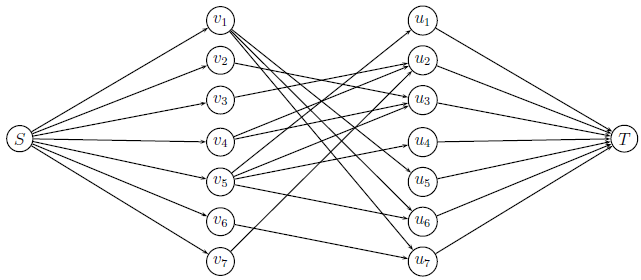
Паросочетания
Паросочетание — подмножество рёбер двудольного графа, никакие два из которых не смежны между собой.
Насыщенная вершина — вершина, инцидентная ребру из паросочетания.
Свободная вершина — вершина, не инцидентная ребру из паросочетания.
Совершенное паросочетание — паросочетание, где все вершины графа насыщенные.
Алгоритм построения максимального паросочетания двудольного графа
Ввести фиктивные вершины и
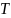 ,
соединив S с вершинами
первой доли, а T — второй
доли.
,
соединив S с вершинами
первой доли, а T — второй
доли.Ориентировать все рёбра от S к первой доле, от первой доли ко второй, от второй доли к T.
Пока существует путь от S к T
Изменить ориентацию рёбер вдоль этого пути
Удалить рёбра, инцидентные фиктивным вершинам
Рёбра, ориентированные от второй доли к первой — искомое паросочетание.
21: Остовные деревья. Алгоритм Прима.
стр. 292
Алгоритм ищет минимальное остовное дерево графа.
Остовное дерево — дерево, являющееся подграфом графа и содержащее все его вершины.
Алгоритм.
22: Остовные деревья. Алгоритм Краскала.
Алг. 2.16 стр. 294-296
Остовное дерево — дерево, являющееся подграфом графа и содержащее все его вершины.
23: Алгоритм Дейкстры
Ищет минимальный путь между источником и остальными вершинами.
Инициализация:
Устанавливаем всем вершинам длину пути на максимальную.
Устанавливаем источнику длину пути на 0.
Основной алгоритм:
Пока есть необработанные вершины
Находим необработанную вершину , у которой кратчайшая длина пути.
Для всех смежных с вершин :
Изменяем текущую длину пути до на сумму длины и длины пути до , если эта сумма меньше.
Помечаем вершину обработанной.
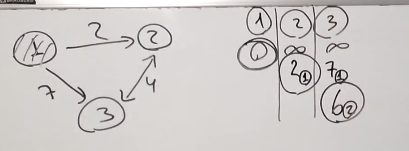
Теорема.
Алгоритм Дейкстры ищет кратчайшие пути
от источника до остальных
вершин.
Доказательство.
Рассмотрим
минимальный путь
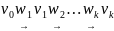 На
первом шаге алгоритма
На
первом шаге алгоритма
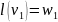 Заметим,
что сопоставляемая длина пути может
только уменьшаться в процессе.
Когда
мы начинаем обрабатывать
Заметим,
что сопоставляемая длина пути может
только уменьшаться в процессе.
Когда
мы начинаем обрабатывать
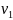 ,
то к этому моменту
,
то к этому моменту
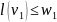 ,
а для
,
а для
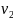 путь станет
путь станет
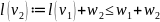 .
Получается
при обработке
.
Получается
при обработке
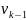 для
для
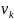 путь станет
путь станет
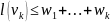 .
Но
так как мы рассматриваем минимальный
путь, то
.
Но
так как мы рассматриваем минимальный
путь, то
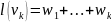 .
Значит
алгоритм действительно работает
корректно.
.
Значит
алгоритм действительно работает
корректно.
24: Алгоритм Флойда
Алгоритм находит все кратчайшие пути между всеми парами вершин.
Инициализация:
 — матрица смежности взвешенного графа
(«0» — диагональ, ∞ — нет ребра, остальное
— есть ребро).
— матрица смежности взвешенного графа
(«0» — диагональ, ∞ — нет ребра, остальное
— есть ребро).
Алгоритм
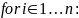
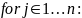
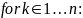
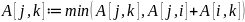
Доказательство индукцией по количеству рёбер в пути.
