7: Гамильтоновы графы. Гамильтоновость и точки сочленения. Теоремы Дирака и Оре. Гамильтоновы графы

Гамильтонов путь — простой путь, включающий все вершины.

Гамильтонов цикл — простой цикл, включающий все вершины.

Полугамильтонов граф — граф, имеющий гамильтонов путь.

Гамильтонов граф — граф, имеющий гамильтонов цикл.

Гамильтоновость и точки сочленения

Точка сочленения — вершина, при удалении которой увеличивается количество компонент связности графа.

Утверждение. Если в графе есть точка сочленения, то граф не гамильтонов. Объяснение. Начнём обход графа с точки сочленения по одной из сторон. Так как снова пройти через точку сочленения невозможно, то невозможно построить гамильтонов цикл.

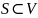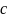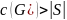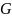Теорема. Рассмотрим множество . Обозначим за количество компонент связности графа. Если , то граф не гамильтонов. Если 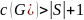, то граф не полугамильтонов. Доказательство. Заметим, что компоненты связности графа 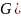связаны вершинами из 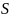. Рассмотрим гамильтонов цикл, разделённый вершинами из . Заметим, что вершины разбивают цикл на 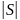путей. Каждый путь проходит по вершинам только одной компоненты связности графа , поэтому количество путей не превосходит количество компонент связности графа .

Аналогично, рассмотрим гамильтонов путь. В этом случае частей будет 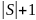. Каждая часть принадлежит только одной компоненте связности графа , поэтому количество путей не превосходит количество компонент связности графа .

Теоремы Дирака и Оре

Теорема Оре

Если для любых несмежных вершин и графа порядка 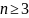(число вершин в графе) выполняется 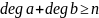, то граф — гамильтонов (другими словами: сумма степеней любых двух несмежных вершин не меньше общего числа вершин в графе).

Теорема Дирака

Если для любой вершины графа порядка выполняется 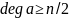, то граф — гамильтонов.

8: Деревья. Несколько эквивалентных определений дерева

Дерево — связный граф без циклов.

Лес — произвольный граф без циклов.

Висячая вершина или лист — вершина степени 1.

Остовное дерево — дерево, являющееся подграфом графа и содержащее все его вершины.

Дерево — граф, любые две вершины которого соединены простой цепью.

Дерево — граф без циклов с числом вершин на единицу большим числа рёбер.

9: Код Прюфера

Код Прюфера — последовательность из 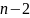чисел (от 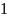до ) с возможными повторениями, кодирующая структуру дерева.

Алгоритм построения кода Прюфера

Выбирается концевая вершина с наименьшим номером, и в код записывается номер единственной вершины, с которой она соединена. Концевая вершина удаляется. Процесс идёт до тех пор, пока не останется две вершины.

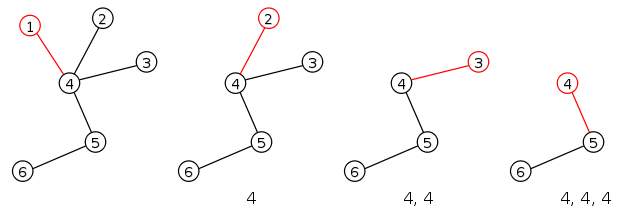
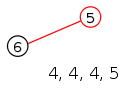
Алгоритм восстановления дерева по коду Прюфера

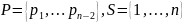
Выбирается минимальный номер 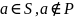. Добавляется ребро , а сами и 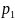удаляются из списков. Процесс повторяется до тех пор, пока не станет пустым. Добавляется ребро вершин с оставшимися номерами из .

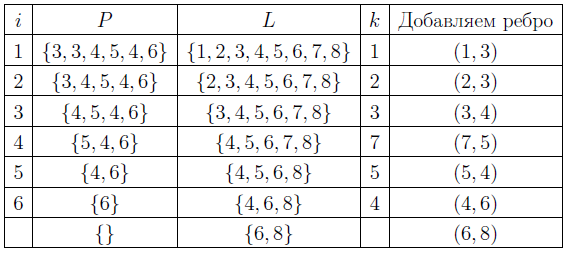
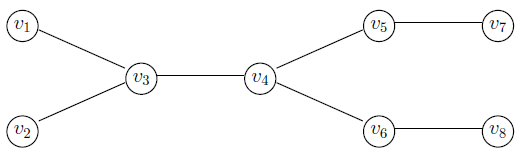
10: Цикломатическое число графа. Теорема Эйлера. Планарные графы

Цикломатическое число графа

Цикломатическое число графа — минимальное число рёбер, удаление которых разрушает все циклы графа, превращая его в дерево или в лес.

Цикломатическое число графа — количество независимых циклов в графе.

Вычисляется: 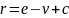— число рёбер 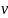— число вершин — число компонент связности

Планарные графы

Изоморфность графов — взаимно-однозначное отображение, сохраняющее соответствие между рёбрами графов.

Плоский граф — граф, вершины которого — точки, а рёбра — непрерывные плоские линии без самопересечений и пересечений с другими рёбрами.

Планарный граф — граф, изоморфный плоскому графу.

Теорема Эйлера

Грань плоского графа — ограниченная циклом часть плоскости, по которой не проходит ни одна цепь, начало и конец которой принадлежат этому циклу. (также есть неограниченная/внешняя грань)

Теорема. Пусть — плоский связный граф, имеющий вершин, рёбер и 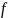граней. Тогда

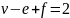
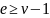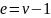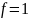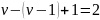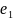Доказательство по индукции. Fix — фиксируем число рёбер. База: Граф связен, значит . Пусть , тогда — дерево, значит циклов нет, тогда . Индукционный переход: Пусть теорема справедлива для всех . Докажем теорему для . Т. к. 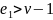, значит есть цикл. Пусть 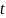— некоторое ребро этого цикла. Значит принадлежит двум граням. Удалим его. Тогда грани сольются в одну, а граф останется связен. Новый граф имеет вершин, 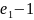рёбер и 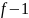граней. Значит . 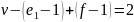Тогда .
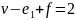