11: Применения формулы Эйлера: непланарность k5 и k33 Следствие теоремы Эйлера

Пусть — плоский связный граф, имеющий вершин, рёбер и граней. Тогда при 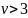справедливо .

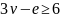Доказательство. Пусть 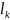— число граней, ограниченных 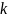рёбрами. Поскольку нет петель и кратных рёбер, то каждая грань ограничена минимум тремя рёбрами: 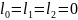Общее число граней: 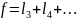Общее количество рёбер (при такой подсчёте каждое ребро учитывается дважды): 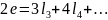Отсюда получаем:

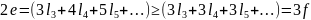
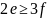По теореме Эйлера:

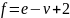
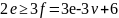
Непланарность k5

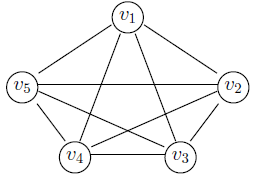
Для этого графа 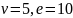. Если бы граф был плоским, тогда по следствию , но 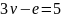— противоречие, доказывающее непланарность графа.

Непланарность графа k3,3

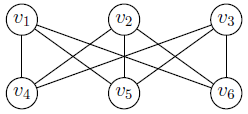
Для этого графа 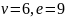. Если бы граф был плоским, то число граней должно быть 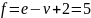. В этом графе нет циклов длины 3, поэтому 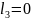, значит должно выполняться: 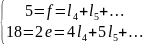Очевидно, что 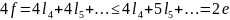Однако 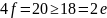Возникло противоречие, доказывающее непланарность графа.

12: Обход в ширину

Сначала просматриваются все соседние вершины, затем соседи соседей и т. д. Используется принцип FIFO (очередь).

1. Добавляем в очередь и список просмотренных вершин произвольную вершину

2. Пока очередь не пуста

   1. Посмотреть на текущую вершину в очереди

   2. Если вершина смежная с какой-нибудь не просмотренной вершиной

1. Добавить в очередь и просмотренные вершины

3. Иначе

   1. Удалить вершину из очереди

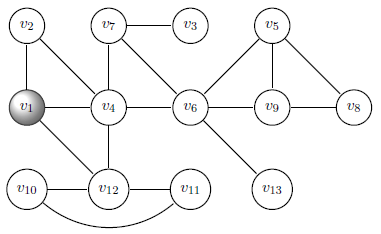
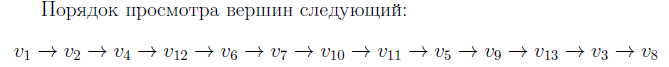
13: Обход в глубину

Идти вглубь, пока это возможно, а когда стало невозможно, возвращаться и искать другой путь. Используется принцип LIFO (стек).

2. Записываем в стек и список просмотренных вершин произвольную вершину

3. Пока стек не пуст

   1. Посмотреть на текущую вершину в стеке

   2. Если вершина смежная с какой-нибудь не просмотренной вершиной

      1. Записать в стек и в просмотренные вершины

   3. Иначе

      1. Удалить вершину из стека

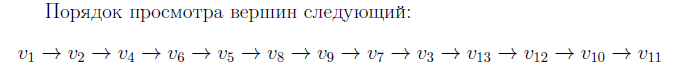
14: Центр, радиус и диаметр графа

Расстояние 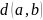— число рёбер в кратчайшем пути от до

Эксцентриситет 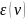— расстояние до самой удалённой вершины от

Пусть — связный неориентированный граф

Диаметр — наибольший из всех эксцентриситетов

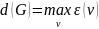
Радиус — наименьший из всех эксцентриситетов

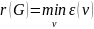
Центральная вершина — вершина, у которой наименьший эксцентриситет

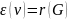
Центр — множество центральных вершин

Теорема.

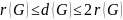
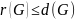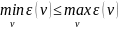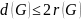
Доказательство. , то есть — очевидно 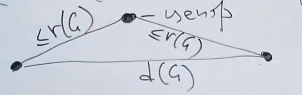От центра до любой вершины расстояние не больше радиуса графа. Таким образом, если мы проведём путь между крайними вершинами через центр, то диаметр не будет превосходить двух радиусов.

Теорема. Центр дерева — 1 вершина или 2 соседние, лежащие(ая) на диаметре.

Доказательство. Рассмотрим диаметр дерева. Для вершин, лежащих на диаметре, расстояние до одной из крайних вершин 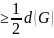. Рассмотрим вершину вне диаметра. Поскольку граф — дерево, то от вершины сущесвтует единственный путь до диаметра в вершину . Получается, что расстояние от до одной из крайних вершин (пусть это будет 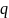) больше 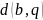и больше расстояния до центра. Таким образом, действительно образуется центр дерева.

Теорема. — дерево. 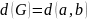, где — самая удалённая от , — самая удалённая от .

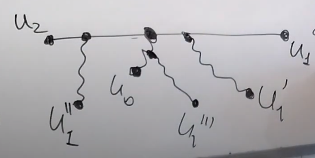Доказательство такое, что расстояние от крайней вершины диаметра, до вершины со штрихом меньше по определению диаметра. Тогда самое удалённое расстояние от вершины не может быть до вершины со штрихом.