15: Сильная связность. Граф конденсации. Сильная связность
Сильная
связность — отношение двух узлов,
показывающее существование ориентированных
путей между ними в обе стороны (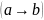
и
)
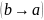Сильносвязный граф — оргаф, у которого любые два узла сильно связаны
Компонента сильной связности — ориентированный подграф, порождённый классом эквивалентности по сильной связности, то есть максимальный по включению сильно связный подграф
(Слабосвязный граф — орграф, у которого при убирании ориентации дуг получается связный граф)
Граф конденсации
Граф
конденсации орграфа
— орграф
,
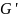вершины которого — это компоненты
сильной связности
,
а дуга в
между вершинами проводится, если в
существует хотя бы одна дуга между
вершинами, входящими в соответсвующие
компоненты сильной связности.
Теорема.
Граф конденсации не содержит
циклов.
Доказательство.
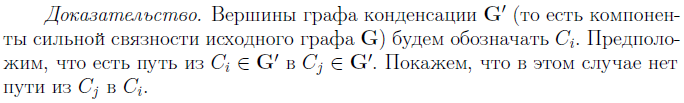
Теорема.
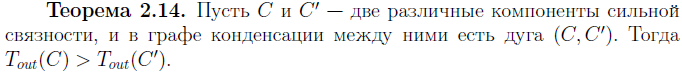
16: Алгоритм Косарайю
Алгоритм ищет компоненты сильной связности орграфа.
Начинаем поиск в глубину.
По мере выхода вершин из стека, записываем время их выхода.
Строим транспонированный граф исходного графа.
Сортируем вершины в порядке убывания их времени выхода.
Для каждой вершины в отсортированном порядке запускаем поиск в глубину. Вершины, найденные поиском входят в компонент сильной связности. (Найденные вершины игнорируются)
…
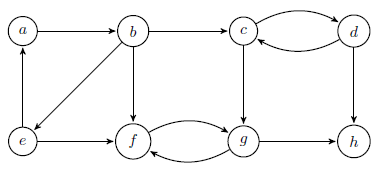
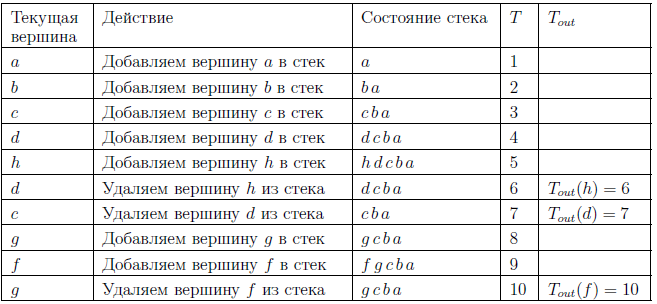
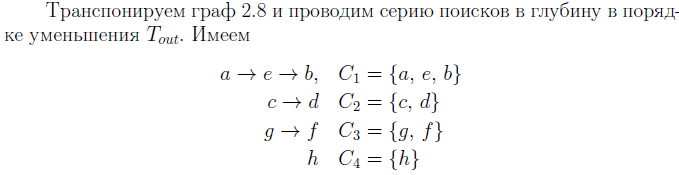
17: Раскраски графов. Хроматический многочлен.
Раскраска
графа — отображение
,
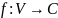где
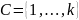— множество «цветов»,
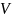— вершины.
Правильная раскраска — раскраска смежных вершин в различный цвет.
Хроматическое
число — наименьшее количество цветов
,
в которые граф можно правильно раскрасить.
(обозначение —
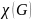[хи])
Хроматический
многочлен
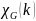— количество правильных раскрасок
графа G в k
цветов.
Утверждение.
Если G — полный граф, то
.
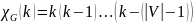Объяснение.
Первую вершину можно покрасить в k
цветов, вторую на 1 меньше, и т. д.
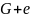— добавление ребра в граф
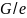— объединение вершин, инцидентных
ребру, в одну
Теорема.
Пусть
— граф,
— ребро, соединяющее вершины
и
,
но отсутствующее в графе,
тогда
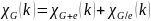Доказательство.
Рассмотрим
раскраски, при которых
и
окрашены в разные цвета. Количество
таких раскрасок равно хроматическому
многочлену графа с добавленным ребром
(то есть
).
Рассмотрим
раскраски, при которых
и
окрашены в одинаковые цвета.
Количество таких раскрасок равно
хроматическому многочлену графа с
объединёнными вершинами
и
(то есть
).
Получается,
что общее количество раскрасок —
и с разными, и с одинаковыми цветами
и
— равно
.
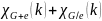Следствие. — многочлен. Доказательство индукцией по количеству антирёбер (множество пар вершин, не соединённых рёбрами).
База:
Пусть
,
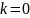значит это полный граф, тогда
.
Переход:
Пусть
—граф без
рёбер. Тогда
— граф без
рёбер, а
— граф без
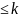рёбер. Значит, как минимум одно антиребро
исчезло.
Получается, что индукционному
предположению слагаемые
и
— многочлены, значит
также многочлен.
<дописать про остальные следствия http://www.youtube.com/watch?v=5T5oFuRVorQ>
18: Хроматический многочлен дерева и цикла.
https://youtu.be/5T5oFuRVorQ?t=1644
19: Сети и потоки. Теорема Форда-Фалкерсона. Алгоритм Форда-Фалкерсона. Алгоритм поиска максимального потока в плоском графе. Сети и потоки
Сеть — положительно взвешенный орграф, в котором существует ровно одна вершина-источник, в которую не входят рёбра, и ровно одна вершина-сток, из которой не выходят рёбра.
Веса означают пропускную способность рёбер.
Поток — функция в сети, сопоставляющая каждому ребру неотрицательное число (величину потока) так, чтобы оно не превышало пропускную способность ребра и для каждой вершины, кроме источника и стока, сумма входящих потоков была равна сумме выходящих.
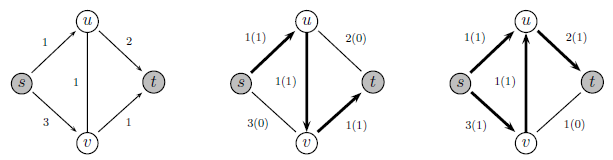
Разрез
— множество рёбер, соединяющих вершины
непересекающихся множеств
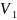и
,
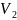где
.
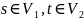Дивергенция потока — разность суммарных потоков через входящие и выходящие в вершину рёбра.
Пропускная способность разреза— сумма пропускных способностей рёбер разреза.
Величина потока через разрез — разность суммы потоков рёбер P+ и суммы потоков рёбер P-.
Величина потока не зависит от выбора разреза (это теорема) и равна дивергенции источника.
Алгоритм строит поток.
находит максимальный поток в сети
Инициализация:
Для каждого
ребра приравниваем поток нулю.
Алгоритм: