0: Определения, способы задания графов. Определения

(Неориентированный) граф — пара множеств: множество вершин 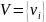и множество рёбер

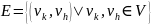
Порядок — число вершин графа (обозначается )

Петля — ребро у которого конец и начало совпадают

Параллельные рёбра — рёбра, соединяющие одну и ту же пару вершин

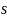-граф — граф, у которого максимальное число параллельных рёбер равно

Если 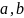— концы ребра 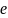, то инцидентно вершинам , а сами вершины смежные.

Полный граф — граф, у которого любые две вершины смежные

Звезда вершины — рёбра, инцидентные этой вершине; если их 0, то вершина изолирована, если 1 — висячая.

Способы задания графов

Матрица инцидентности

Матрица, где строки — вершины, а столбцы — рёбра. Смежные вершины в столбце ребра 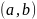помечаются 1 (если орграф: -1 в начало и 1 в конец).

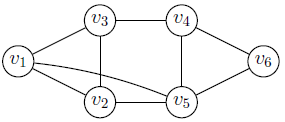
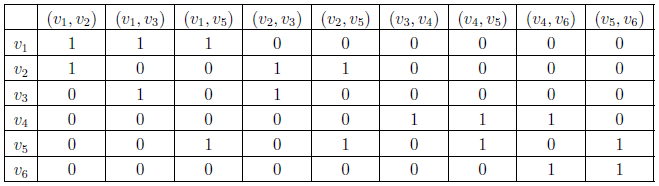
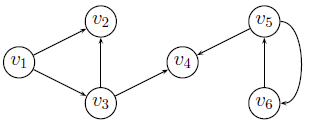
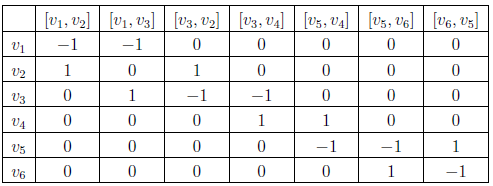
Матрица смежности

Матрица, где строки и столбцы — вершины. Ребро 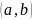помечается 1 в пересечениях вершин 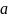и в матрице.

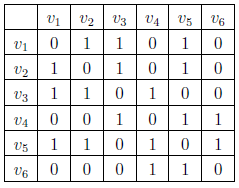
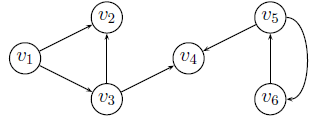
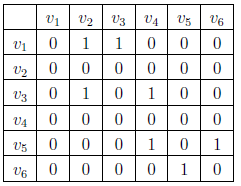
Списки смежности

Массив, состоящий из списков, относящихся к каждой вершине. Эти списки содержат вершины, инцидентные к этой вершине.

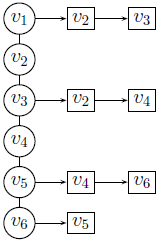
Список рёбер

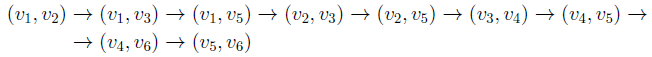
1: Бинарные отношения. Свойства бинарных отношений. Как их проверять по матрице и графу?

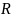Бинарное отношение на множестве — подмножество множества 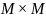Если элемент находится в отношении с другим элементом, то значит, что пара этих элементов находится в подмножестве .

Рефлексивность — 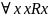(операция ) Диагональ из «1». Петля у каждого узла.

Антирефлексивност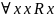ь — (операция ) Диагональ из «0». Нет петель.

Симметричность — (операция ) Матрица симметрична. Все рёбра в обе стороны.

Асимметричность — 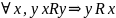(операция ) Диагональ из «0». Нет симметричных «1». Нет петель. Все рёбра в одну сторону.

Антисимметричность — 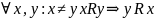(операция , 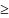) Нет симметричных «1». Все рёбра в одну сторону.

Транзитивность — 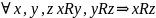(операция , ) Если из можно вдоль дуг попасть в , то должна быть дуга, непосредственно их соединяющая.

2: Отношения эквивалентности. Классы эквивалентности.

339-341

Отношение эквивалентности — отношение, обладающее рефлексивностью, симметричностью и транзитивностью.

Класс эквивалентности — подмножество элементов, находящихся в отношении эквивалентности с элементом . На графе это выглядит как компонента сильной связности.

3: Отношения порядка. Диаграмма Хассе. Топологическая сортировка.

341-346

Отношение нестрогого порядка — отношение, обладающее рефлексивностью, антисимметричностью и транзитивностью. (операция )

Отношение строгого порядка — отношение, обладающее асимметричностью и транзитивностью. (операция )

Линейность порядка —  (операция )

Топологическая сортировка

Топологическая сортировка по отношению частичного порядка строит согласованное с ним отношение линейного порядка (но не обязательно).

1. Цикл по 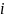в диапазоне

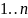
   1. Найти минимальный элемент множества и переместить в созданный список, удалив из текущего.

Топологическая сортировка упорядочивает вершины ориентированного графа в порядке, не нарушающем направление дуг.

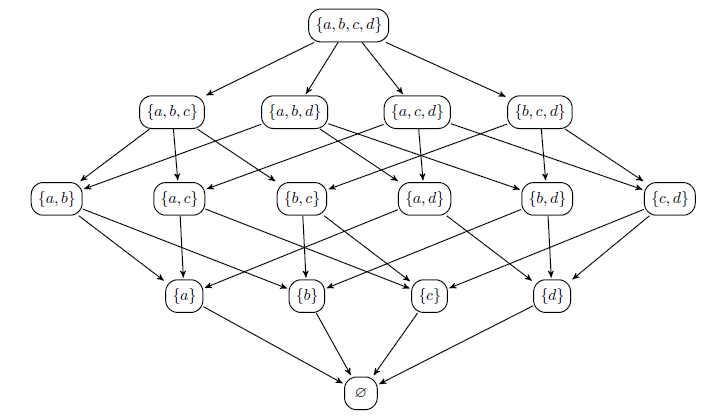
Диаграмма Хассе

Строится для упорядоченного множества. Если элемент непосредственно следует за , то рисуется дуга от вершины к .

4: Рефлексивное, симметричное, транзитивное замыкания. Способы построения.

346-351

Замыкание по свойству 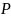— минимально возможное отношение 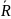, обладающее свойством и содержащее в себе подмножество .

Пример:

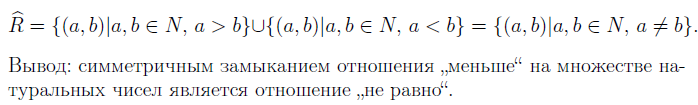
Рефлексивное замыкание

На графе построить везде петли. В матрице — добавить «1» на главную диагональ.

Симметричное замыкание

На графе сделать рёбра в обе стороны. В матрице сделать её симметричной.

Транзитивное замыкание

На графе дополнить дугами , если из можно попасть в (другим путём). По матрице построить матрицу достижимости 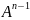, где 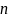— количество элементов в .

5: Пути и циклы в графе. Связность. Компоненты связности

Пути и циклы в графе

Путь — последовательность вершин и рёбер между ними

Открытый путь — путь, где концевые вершины пути не одинаковы

Замкнутый путь — путь, где концевые вершины пути одинаковы

Простой путь — путь, где рёбра не повторяются

Простая цепь (или -цепь) — путь, где вершины (а значит и рёбра) не повторяются

Простой цикл — замкнутый путь, где вершины не повторяются (кроме концевых)

Связность

Связность — отношение двух вершин, показывающее существование пути между ними

Связный граф — граф, у которого любые две вершины связаны.

Компоненты связности

Связность вершин является отношением эквивалентности:

1. рефлексивность: путь 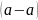существует для любого

2. симметричность: пути 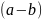и

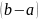
3. транзитивность: соединяя последовательно цепи 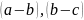, получаем цепь

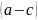
Компонента связности — подграф, порождённый классом эквивалентности по связности, то есть максимальный по включению связный подграф

6: Эйлеров путь и цикл

Эйлеров путь — простой путь (т. е. рёбра не повторяются), включающий все рёбра графа.

Граф, имеющий замкнутый эйлеров путь, — эйлеровый, а разомкнутый — полуэйлеровый.

Теорема. Эйлеров цикл существует тогда и только тогда, когда граф связный и все его вершины имеют чётную степень.

Следствие. Эйлеров путь существует тогда и только тогда, когда граф связный и существует ровно две вершины нечётной степени.

Алгоритм поиска замкнутого эйлерового пути

1. Записать в стек произвольную вершину

2. Пока стек не пуст

   1. Посмотреть на текущую вершину в стеке (a)

   2. Если есть ребро (a, b) с любой вершиной b

      1. Записать вершину b в стек

      2. Удалить ребро (a, b) из графа

   3. Иначе

      1. Удалить вершину a из стека

      2. Записать вершину a в последовательность эйлерова цикла