Коды Адамара - Доклад

Коды Адамара

Жак Адамар (1865-1963) - один из крупнейших французских математиков конца XIX и первой половины XX века, автор ряда основополагающих работ в области теории чисел, алгебры и математического анализа.

Важную роль в алгебре и комбинаторике играют матрицы Адамара, которые впервые были введены в математический обиход в конце прошлого века ^*). Сравнительно недавно, в 1960 г., было замечено, что эти матрицы могут быть использованы для построения кодов с большим кодовым расстоянием

Квадратная матрица Н порядка n с элементами ±1 называется матрицей Адамара, если выполняется условие

НH^T = nЕ_n.

Вот несколько примеров матриц Адамара:

(1),

n = 1

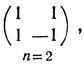
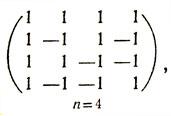
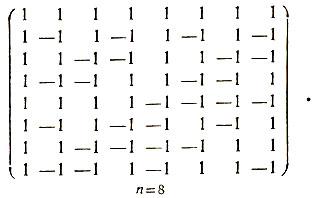
Рассмотрим произвольную матрицу Адамара

h_ij = ± 1.

Из определения следует, что для любой пары строк с номерами i и j (i ≠ j) верно равенство:

h_i1h_j1 + h_i2h_j2 + ... + h_inh_jn = 0. (1)

Таким образом, различные строки матрицы Адамара попарно ортогональны. Далее, число слагаемых в (1), равных +1, должно совпадать с числом слагаемых, равных -1. Следовательно, n четно и любые две строки совпадают ровно в n/2 позициях и различаются в остальных.

Пусть теперь А - двоичная матрица, получающаяся из матрицы Н заменой элемента +1 на 0 -1 на 1. Множество векторов-строк матрицы А образует тогда код с расстоянием Хемминга между любыми кодовыми словами, равным n/2. Так, из матрицы Адамара порядка 8 получаем матрицу A, задающую код длины 8 с кодовым расстоянием 4:

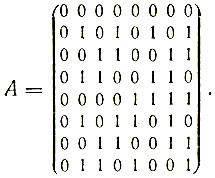
Не меняя кодового расстояния, можно уменьшить длину кода, если отбросить первый (нулевой) символ каждого слова.

Указанным образом из всякой матрицы Адамара порядка n можно получить двоичный код Адамара типа (n-1, n, n/2) (n-1 - длина кодового слова, n - число слов кода, n/2 - кодовое расстояние). Это, как правило, код, не являющийся линейным.

С матрицей А связаны еще два кода, которые тоже называют кодами Адамара.

Первый из них получается так. Перейдем от матрицы А к матрице A‾, заменив все элементы матрицы A их дополнениями (т. е. заменив единицы нулями, а нули - единицами). Тогда строки матриц A и A‾ в совокупности образуют код типа (n, 2n, n/2), что легко проверяется с помощью равенства (1).

Другой код Адамара получается из предыдущего отбрасыванием первого символа в каждом кодовом слове. Это будет код типа (n - 1, 2n, n/2 - 1).

Например, из матрицы (2) можно получить таким способом коды Адамара типов (8, 16, 4) и (7, 16, 3).

Коды Адамара, как видно из их определения, обладают интересной особенностью: расстояние между любыми двумя кодовыми словами одинаково и совпадает поэтому с кодовым расстоянием. Подобные коды называют эквидистантными, и в некоторых случаях их использование дает особые преимущества.

Коды Адамара, обладая большим кодовым расстоянием, позволяют соответственно исправить и большое количество ошибок (первые два из них исправляют ошибки примерно в четверти позиций кодового слова). Достигается это, конечно, ценой высокой избыточности.

Для построения и реализации кода Адамара той или иной длины необходимо построить сначала матрицу Адамара соответствующего порядка. Надо сказать, что такое построение является совсем нелегким делом, и этому вопросу посвящен внушительный раздел современной комбинаторики. Некоторые методы построения будут рассмотрены ниже в разделе "Задачи и дополнения" (см. также [4]).

С матрицами Адамара связан ряд нерешенных проблем, одна из которых состоит в следующем. Мы уже видели, что порядок n матрицы Адамара при n ≥ 3 может быть лишь четным. Более того, нетрудно доказать, что при n ≥ 4 порядок обязан делиться на 4. До настоящего времени остается открытым вопрос: для любого ли n, кратного 4, существует матрица Адамара порядка n? Неизвестно, в частности, существует ли матрица Адамара порядка 268 (это наименьший порядок, кратный 4, для которого матрица Адамара еще не построена).

Задачи и дополнения

1. Укажем наиболее простой способ построения матриц Адамара сколь угодно больших порядков. Пусть Н_n - матрица Адамара порядка n и -Н_n - матрица с противоположными элементами. Составим из них матрицу порядка 2n следующим образом:

Именно таким образом получались одна из другой матрицы порядков 1, 2, 4, 8, приведенные в начале этого параграфа.

Доказать, что матрица Н_2n является матрицей Адамара.

2. Следующие две операции преобразуют матрицу Адамара снова в матрицу Адамара:

1) перестановка строк (или столбцов);

2) умножение строки (или столбца) на -1.

С помощью этих операций любую матрицу Адамара можно преобразовать в так называемую нормализованную матрицу Адамара, у которой первая строка и первый столбец состоят из одних единиц.

3. Изложим еще один метод построения матрицы Адамара - метод Пэли. Рассмотрим поле Z_р вычетов по модулю р, где р - простое число. Всякий элемент Z_p, являющийся квадратом какого-либо элемента того же поля, называется квадратичным вычетом, всякий другой - квадратичным невычетом. Определим на Z_p следующую функцию χ‾(i), называемую символом Лежандра ^*):

Исходя из этого определения, можно доказать, что для всякого с ≠ 0 выполняется равенство

χ(1‾) χ(‾1 + ‾c) + χ(2‾) χ(‾2 + ‾c) + ... + χ(p-1)‾ χ (p-1‾ + c‾) = -1. (3)

Рассмотрим теперь квадратную матрицу Q порядка р, элементы которой q_ij (i, j = 1, 2, ..., р) определяются следующим образом:

q_ij = χ(j‾ - i‾).

Пусть Е - единичная матрица порядка р, a J - квадратная матрица того же порядка, все элементы которой равны 1. Тогда, пользуясь (3), можно доказать равенства

QQ^T = pE - J, QJ = JQ = 0. (4)

Пусть теперь p = 4k - 1. В этом случае матрица

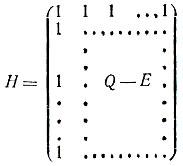
является матрицей Адамара порядка p + 1. Действительно, вычисляя произведение НН^Т, получаем:

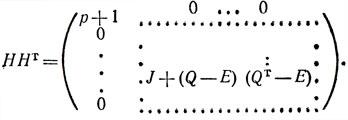
Далее, как нетрудно проверить, матрица Q порядка р = 4k - 1 совпадает с матрицей -Q^T. Отсюда с учетом (4) имеем:

J + (Q - E) (Q^T - E) = J + QQ^T - Q - Q^T + E = J + pE - J - Q + Q + E = (p + 1)E.

Таким образом, HH^T = (р + 1)E.