Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

abzalilov_malakaev_shirokova_

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

544.3 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

неопределенностей невозможно сразу сказать о том, существуют или нет иско• мые пределы, не говоря уже о нахождении их значений, если они существуют.

6.1. Раскрытие неопределенностей типа	0	.	Для раскрытия та•

	0

кой неопределенности обычно используется метод разложения на множители числителя и знаменателя с последующим сокращением одинаковых множите• лей.

Пример 1. Найти lim

x2 − 3x + 2

. Имеем неопределенность типа

x2 − 1

x→1

Разложим на множители числитель и знаменатель:

lim

x2 − 3x + 2

= lim

1)(x − 2)

(x −

x→1

−

x→1

1)(x + 1)

−

= lim

x − 2

1 − 2

−

1 + 1

→

1 x + 1

Пример 2.

Найти lim

√

. Для разложения знаменателя на мно•

1 + 3x − 1

→

жители используем прием умножения обеих частей на сопряженное к знамена•

телю выражение:

√

x→0

x( 1 + 3x + 1)

√1 + 3x − 1

0 = x→0 (√1 + 3x − 1)(√1 + 3x + 1)

lim

√

= lim

x( 1 + 3x + 1)

= lim

1 + 3x + 1

1 + 0 + 1

x→0 (1 + 3x − 1)

x→0

6.2. Раскрытие неопределенностей типа

∞

. Для

раскрытия

неопределенности этого типа обычно используется методn

∞деленияo

числителя и

знаменателя на наивысшую степень переменной.

Пример 3. Найти lim

x − 3x2

. Имеем неопределенность типа

∞

. Наи•

x→∞ x2 + 1

высшая степень числителя и знаменателя равна двум. Делим числительn∞oи зна•

менатель на x2:

lim

x − 3x2

∞

= lim

x1 − 3

0 − 3

x→∞

x2 + 1

∞o

x→∞

1 +

1 + 0

−

Здесь мы учли, что

= 0:

∞

Пример 4. Найти lim

(x − 1)2

. Выделяем наивысшие степени числителя

√

+ 4

и знаменателя:

→∞

n∞o

lim

(x − 1)2

∞

= lim

1 − x1

= lim

1 − x1 2

+ 4

→∞ √x

→∞ x 1 +

→∞ 1 1 + 42

(1 − 0)2

0√1 + 0

∞

Неопределенности остальных типов обычно сводят к неопределенностям ти•

∞o

па

∞

путем алгебраических преобразований.

6.3. Задания к теме. Найти пределы:

lim

x2 − 4x + 1

lim

x − 3

lim

tg x

x→2

2x + 1

x→3 x2 − 2x + 3

√

x→π sin 2x

lim

3x − 1

5. lim

x3 − 1

lim

− 6x

2 − 9

x→∞ x

x→∞ x2 + 5

x→∞

3x + 1

√1 + x −

√1 − x

lim

8. lim

√x − 1

x→0

x→1

√x − 1

lim

3x + 6

10.

lim

9 − x2

x→−2

x3 + 8

x→3

√3x − 3

11. lim

5x2 − 3x + 2

12. lim

3x + 1

2x2 + 4x + 1

x→∞

√3x2 + 1

Ответы: 1. 51 . 2. 21 . 3. 21 . 4. 0. 5. ∞. 6. 2. 7. 1. 8. 32 . 9. 41 . 10. −12. 11.

. 12.

√

§ 7.		Комплексные числа
Мнимая единица – это число, квадрат которой равен −1:
i	2	√

		= −1 или i = −1.

Комплексные числа – расширение множества вещественных чисел. Любое комплексное число z может быть представлено как формальная сумма z = = x + iy, где i – мнимая единица, а x и y – вещественные числа, называемые действительной и мнимой частями соответственно: x = Re z, y = Im z.

Если для геометрической интерпретации вещественных чисел использова• лась числовая прямая, то для интерпретации комплексных чисел используется плоскость, где по оси абсцисс откладывается действительная часть, а по оси ординат – мнимая.

z = 5 + 3i 3

−3

z = 5 − 3i

Комплексно сопряженным числом к z = x+iy называется число z = x−iy. Например, для числа z = 5 + 3i комплексно сопряженным будет z = 5 − 3i.

С комплексными числами тесно связана основная теорема алгебры, которая гласит, что алгебраическое уравнение порядка n

zn + an−1zn−1 + . . . + a1z + a0 = 0

с комплексными коэффициентами ak имеет ровно n комплексных корней: z1, z2,

. . . , zn. Если все коэффициенты ak вещественные, корни уравнения будут либо чисто вещественные числа, либо пары комплексно сопряженных корней.

Пример 1. Решить квадратное уравнение x2 + 4x + 40 = 0. Вычисляем дискриминант D = 42 − 4 · 40 = −144. Так как D < 0 уравнение не имеет веще• ственных корней, но из основной теоремы алгебры следует, что у квадратного

уравнения есть два корня. Учитывая, что

√

= 12i,

D =

−144 =

144 ·

−1

найдем

√

1,2

−4 ± D

−4 ± 12i

−

6i.

Пример 2. Найти все корни уравнения x3 = 8. Из основной теоремы алгебры следует, что у данного уравнения должно быть три корня:

x3 = 8 x3 − 22 = 0 (x − 2)(x2 + 2x + 4) = 0.

Из условия обращения первой скобки в нуль находим первый корень: x1 = 2, из условия обращения в нуль второй скобки – два остальных:

√

+ 2x + 4 = 0 D = −12 D = 2 3i

√

−2 − 2 3i

−

1 +

−

7.1. Задания к теме. Найти все корни уравнений:

1. x2 + 25 = 0, 2. x2 − 2x + 5 = 0, 3. x3 + 8 = 0,

4. x4 + 5x2 − 36 = 0, 5. x4 + 4x2 + 4 = 0, 6. x4 + 4 = 0,

7. x4 − 6x3 + 10x2 = 0, 8. x4 = 81, 9. x6 + 64 = 0.

Ответы: 1. ±5i. 2. 1 ± 2i. 3. −2, 1 ± √3. 4. ±2, ±3i. 5. ±√2i, ±√2i. 6.

√

±1 ± i. 7. 0, 0, 3 ± i. 8. ±3, ±3i. 9. ±2i, ± 3 ± i.

§ 8. Вычисление производных.

Производной функции f(x) называется функция, обозначаемая как f′(x)

равная пределу отношения
f′(x) = lim		f(x +		x) − f(x)

				x
	x→0
8.1. Таблица производных элементарных функций
1.	(C)′ = 0				2. (xn)′ = nxn−1
3.	(ln x)′ =		1		4. (loga x)′ =	1
			x			x ln a

√31x2 .

5.	(ex)′ = ex				6. (ax)′ = ax ln a
7.	(sin x)′ = cos x				8.	(cos x)′ = − sin x
	1							1
9.	(tg x)′ =				10.	(ctg x)′ = −
9.	(tg x)′ =	cos2 x			10.	(ctg x)′ = −	sin2 x
11.	(arcsin x)′ =			1	12.	(arccos x)′ =			1


			√1 − x2					−	√1 − x2
			√1 − x2					−	√1 − x2
				1					1
13.	(arctg x)′ =				14.	(arcctg x)′ = −
13.	(arctg x)′ =		x2 + 1		14.	(arcctg x)′ = −				x2 + 1

8.2. Правила вычисления производных. Для вычисления производ• ных (или, другими словами, дифференцирования) применяются следующие пра•

вила:
1.	(Cu)′ = Cu′	– вынесение постоянного множителя.
2.	(u + v)′ = u′ + v′	– дифференцирование суммы.
3.	(uv)′ = u′v + uv′	– дифференцирования произведения.

4.u ′ = u′v − uv′ – дифференцирование дроби. v v2

5.Если y = f(u), а u = g(x)), то y(x) = f[g(x)] – сложная функция

(функция от функции). Ее производная y′ = f′(u) · g′(x).
Пример 1. Найти производную функции y = 2x3 − 3 sin x +
Используем первое и второе правила дифференцирования:
		−	√x2	′	−
	′ + (		1	′			2
y′ = 2x3	′ + (		3 sin x)′ +	= 2(x3)′ 3(sin x)′ +		x−	3
			3

′

= 6x2

−

3 cos x

x(−32 −1) = 6x2

−

3 cos x

x−35

= 6x2

−

3 cos x

−

− 3

√x5

Пример 2. Найти производную функции y =

cos x

Используем правило дифференцирования дроби:

y′

cos x

′ =

(cos x)′x2 − cos x(x2)′

(x2)2

(− sin x)x2 − (cos x)2x

−

x sin x + 2 cos x

Пример 3. Найти производную функции y = sin x2.

Здесь y(x) – сложная функция, где внешняя функция f(u) = sin u и внут• ренняя u = g(x) = x2. По правилу дифференцирования сложной функции

y′ = (sin(x2))′ = (sin u)′u · (x2)′x = cos u · 2x = 2x cos x2.

Пример 4. Найти производную y = arctg

x3e2x .

По правилу дифференцирования сложной функции вначале берем произ•

водную от внешней функции (arctg u):

y′ = arctg(x3e2x) ′ =

x3e2x ′ = . . .

1 + (x3e2x)2

Далее нам потребуется формула дифференцирования произведения:

. . . =

· (x3)′e2x + x3 e2x ′ = . . .

1 + x6e4x

Функция e2x также является сложной, поэтому

3x2e2x

+ x3e2x(2x)′

3x2e2x + 2x3e2x

(3 + 2x)x2e2x

. . . =

6 4x

1 + x e

8.3. Задания к теме. Найти производные функций:

1. y =

2. y = 6

√

x − 4

y = x

cos x.

cos x

4. y =

. 5. y = x22x.

6. y = (1 − 5x)4. 7. y = p1 − x2.

√

8. y =

cos 4x.

9. y = arcsin

1 − 4x.

11. y = ln r

1 + 2x

10. y = ln

√x + √x + 1 .

−

12. y = x arctg

−

ln(x2 + a2).

13. y = arctg e2x + ln r

e2x + 1

14. y = x arccos x − 1 − x2.

e2x

−

√

15. y = x2p1 − x2.

16. y =

4 + 1

17. y = √xe√x.

18. y =ln(e2x +

19. y =arccos √

e4x + 1).

2x − 4x2.

1 − 2x

2+2x+3

Ответы: 1.

−

. 2.

−

. 3. x(2 cos x

−

x sin x). 4. (2 cos x

−

√

−x sin x)/x

. 5. 2

(2x+x

ln x). 6. −20(1−5x)

. 7. −

√

. 8. −2 tg 4x cos 4x.

−

√

10.

√

11.

12.

arctg a . 13.

14. arccos x. 15.

−

4x2

−

e8x

x 4x

2 x +1

x(2−3x2)

−

2(3x+1)

e√

2e2x

√

. 16.

−

x3√

. 17.

1 +

√

18.

√

. 19. qx

− 4.

1−x2

4x+1

e4x+1

§9. Исследование функций.

9.1.Исследование возрастания и убывания функции. Функция y = f(x) называется возрастающей (убывающей) на отрезке [a, b], если для

любых x1 и x2 > x1 на этом отрезке f(x1) < f(x2) (f(x1) > f(x2)). Интервалы возрастания и убывания функции называются интервалами монотонности.

Достаточное условие возрастания(убывания) функции. Если функция дифференцируема на этом отрезке и f′(x) > 0, то функция возрас• тает. Если f′(x) < 0, то функция убывает.

9.2. Нахождение точек экстремума функции. Точка x = x0 на• зывается точкой максимума (минимума) для функции y = f(x), если f(x0) является наибольшим (наименьшим) значением функции в некоторой окрестно• сти этой точки. Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – ее экстремумами.

Необходимым условием экстремума является равенство нулю или отсутствие первой производной функции в точке x0, т.е. f′(x0) = 0 или не существует. Эти точки называются критическими.

Первым достаточным условием экстремума в точке x0 является смена знака у первой производной функции при переходе x через точку x0. Если f′(x) при переходе через точку x0 меняет знак плюс на минус, то в точке x0 функция имеет максимум, в противном случае – минимум. Если при переходе через критическую точку производная не меняет знак, то экстремума нет.

Второе достаточное условие экстремума. Пусть функция f(x) име• ет вторую производную в критической точке x0. Если f′′(x0) > 0 (< 0), то точка

x0 является точкой минимума (максимума).

9.3. Исследование выпуклости функции. Функция y = f(x) назы• вается выпуклой вверх (вниз) на интервале (a, b), если касательные к графику функции на этом интервале расположены выше (ниже) графика функции.

Достаточное условие выпуклости функции. Если функция дважды дифференцируема на этом отрезке и f′′(x) > 0, то функция является выпуклой вниз. Если f′′(x) < 0, то функция является выпуклой вверх.

Точки, в которых выпуклость переходит в вогнутость, или наоборот, назы• ваются точками перегиба функции. При переходе через эти точки вторая произ• водная f′′(x) меняет знак.

9.4. Асимптоты к графику функции. Прямая называется асимпто• той к графику функции, если при стремлении к бесконечности расстояние от графика до прямой стремится к нулю.

Асимптоты бывают вертикальными, они показывают поведение функции в окрестности особой точки, когда y → ±∞, и наклонными, дающими представ• ление о поведении функции при x → ±∞. Если a – особая точка, то уравнение вертикальной асимптоты x = a.

Кривая y = f(x) имеет наклонную асимптоту при x → ∞, уравнение кото• рой y = kx + b, если существуют пределы:

xlim	f(x)	= k	и	xlim [f(x) − kx] = b.

	x
→∞				→∞

В случае k = 0 асимптота называется горизонтальной, ее уравнение y = b =

= lim f(x).

x→∞

9.5. План исследования функции и построения ее графика.

1.Область определения функции, ее особые точки, вертикальные асимптоты.

2.Исследование поведения функции при x → ∞. Наклонные (горизонталь• ные) асимптоты.

3.Вид функции (четная/нечетная/общего вида). Периодичность.

4. f(x) = 0		нули функции, интервалы знакопостоянства.
5. f′(x) = 0		точки экстремума, интервалы монотонности.

6. f′′(x) = 0	точки перегиба, интервалы выпуклости.
		4x
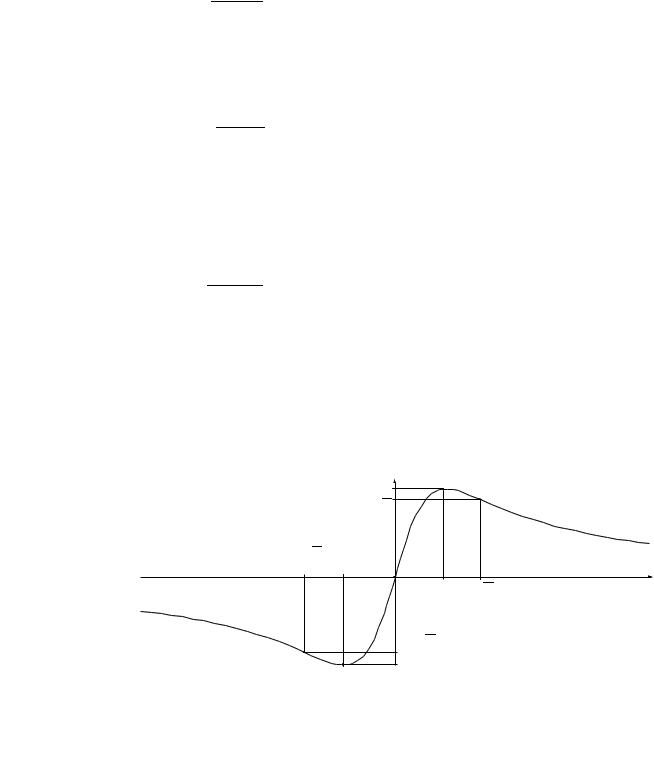
Пример 1. Исследовать функцию y =			и построить её график.

		x2 + 1

1.Область существования функции – вся числовая ось, то есть (−∞, ∞). Следовательно, у этой кривой нет особых точек и вертикальных асимптот.

2.Найдем предел функции при x → ∞:

lim

= lim

= 0

x→∞ x2 + 1

x→∞

1 +

1 + 0

Следовательно, y = 0 – горизонтальная асимптота.

3. f(−x) =

−2

= −f(x). Значит, функция является нечетной

(−x) +1

= −x +1

и ее график симметричен относительно начала координат.

4. f(x) =

= 0 x = 0 – нуль функции. Функция отрицательна при

x2+1

и положительна при x

∞)

(−∞

4(x2

5. f

′(x) =

− 2

= 0

−

1 = 0

x =

1. У функции две критиче•

−(x +1)

ские точки. При x (−∞, −1) (1, ∞) производная f′(x) < 0, следовательно, на этих интервалах функция убывает. При x (−1, 1) f′(x) > 0 функция воз• растает. Точка x = −1 – это точка минимума функции, точка x = 1 – точка

максимума.

√

6. f′′(x) =

8x(2x2−3)3

x = 0илиx =

. При x

= 0

(infty,

−

sqrt3)

√

(x +1)

(0, 3)

вторая производная f′′(x) < 0, на этих интервалах функция выпукла

вверх. На интервалах x

(

sqrt3, 0)

√

) f′′(x) > 0 и функция выпукла

−

( 3,

∞

вниз.

Строим график функции, учитывая точки максимума и минимума, три точ•

ки перегиба и горизонтальную асимптоту:
	2 y
	√
	3
√	−1
− 3	−1	√
	0	√	3	x
	0	1	3

√

− 3 2

9.6. Задания к теме.

Исследовать функцию и построить ее график.

1. y = x2 + 4x + 5, 2. y = 4x −

, 3.

y =

1 + x2

4. y =

x2 − 6x + 13

, 5. y =

, 6. y = x2e−x,

x − 3

x2 − 3

7. y = x3 + 6x2 + 9x, 8. y =

(x − 1)2

, 9. y = xe−x2/2.

x2 + 1

§10. Нахождение наибольших и наименьших значений величин.

1.Решеткой длиной 120м нужно огородить прилегающую к дому прямоуголь• ную площадку наибольшей площади. Определить размеры прямоугольной площадки.

2.В треугольник с основанием a и высотой h вписан прямоугольник наиболь• шей площади. Определите его площадь.

3.Из квадратного листа картона со стороной a вырезаются по углам одинако• вые квадраты и из оставшейся части склеивается прямоугольная коробка. Какова должна быть сторона вырезанного квадрата, чтобы объем коробки был наибольшим?

4.Боковые стороны и меньшее основание трапеции равны 10см. При каком большем основании ее площадь будет наибольшей?

5.Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения равен 18м. При каком радиусе полукруга площадь сече• ния будет наибольшей?

6.В полукруг радиуса R вписан прямоугольник наибольшей площади. Опре• делите его размеры.

7.Из круга вырезан сектор, содержащий угол α, а затем свертывается в конус. При каком угле α объем конуса будет наибольшим.

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.07.201943.44 Кб19кл 2011.docx
#
21.11.2018334.34 Кб1A18.doc
#
09.11.201957.34 Кб4A24.doc
#
26.04.2019716.8 Кб1A6.doc
#
10.02.2015266.85 Кб18Abelyar.rtf
#
10.02.2015544.3 Кб16abzalilov_malakaev_shirokova_.pdf
#
04.12.201831.95 Кб2Access_izmenennyy.docx
#
10.02.20156.8 Mб36acer extensa 5635.pdf
#
10.02.20151.78 Mб36Ace_The_Case_2nd_Ed.pdf
#
10.11.2018246.27 Кб2administr_pravo.doc
#
23.11.201947.1 Кб24Affixation.doc