
- •Определенный интеграл (интеграл Римана) Площадь криволинейной трапеции
- •Определение интеграла Римана, условия его существования
- •Необходимое и достаточное условия существования определенного интеграла
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом Формула Ньютона-Лейбница
- •Интегрирование определенного интеграла по частям
- •12.1. , 12.2., 12.3..
- •Замена переменной в определенном интеграле
- •Вычисление определенного интеграла с помощью максимы
- •Длина дуги кривой
- •Объем тела вращения
- •13.1. , 13.2.,
Интегрирование определенного интеграла по частям
Требуется вычислить
интеграл
![]() ,
где
,
где![]() и
и![]() функции
от
функции
от![]() .
Используя последний вариант формулы
Ньютона-Лейбница, получаем
.
Используя последний вариант формулы
Ньютона-Лейбница, получаем![]() ,
в правой части стоит неопределенный
интеграл, для интегрирования которого
можно использовать формулу
,
в правой части стоит неопределенный
интеграл, для интегрирования которого
можно использовать формулу![]() .
В результате
.
В результате
![]() .
.
Итак, формула интегрирования по частям определенного интеграла
![]() .
.
Пример.
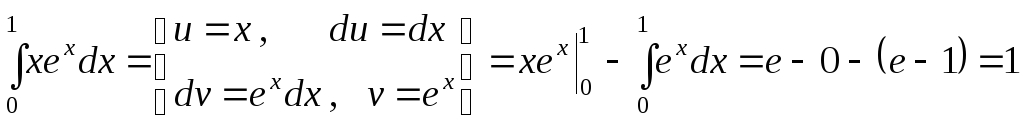 .
.
Примеры для самостоятельного решения
12.1. , 12.2., 12.3..
Ответы. 12.1.
![]() , 12.2.
, 12.2.![]() ,
12.3.
,
12.3.![]() .
.
Замена переменной в определенном интеграле
Замену переменной
в определенном интеграле можно осуществить
двумя способами. Первый – непосредственное
применение формулы Ньютона-Лейбница,
то есть переход от определенного
интеграла к неопределенному
![]() ,
затем замена переменной в неопределенном
интеграле, его вычисление, возвращение
к старой переменной
,
затем замена переменной в неопределенном
интеграле, его вычисление, возвращение
к старой переменной
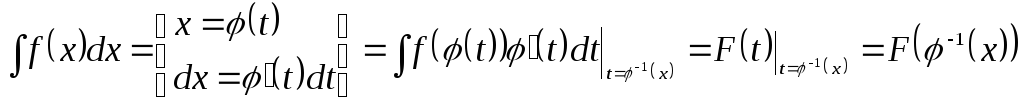
и подстановка верхнего и нижнего пределов интегрирования в соответствии с формулой Ньютона Лейбница
![]() .
.
Здесь
![]() первообразная
функции
первообразная
функции![]() ,
а
,
а![]() обратная
функция функции
обратная
функция функции![]() .
.
Возможен и другой
путь, основанный на том, что в отличие
от неопределенного интеграла, когда
результатом вычисления является функция,
определенный интеграл представляет
собой число. Введем обозначения
![]() ,
тогда
,
тогда
![]()
![]() .
.
Отсюда имеем
![]() .
.
Но![]() первообразная
функции
первообразная
функции![]() ,
следовательно,
,
следовательно,
![]() ,
,
откуда следует формула, реализующая замену переменной без возвращения к старой переменной
![]() .
.
Другими словами,
вместо возвращения к старой переменной
осуществляется корректировка пределов
интегрирования в интеграле после замены
переменной. В процессе этой корректировки
устанавливается, каковы пределы
интегрирования по новой переменной
![]() ,
если пределы интегрирования по старой
переменной от
,
если пределы интегрирования по старой
переменной от![]() до
до![]() .
.
Замечание. Поскольку при любом способе интегрирования осуществляется переход от определенного интеграла к неопределенному, все теоретические наработки, связанные с заменой переменной в неопределенном интеграле, справедливы и при замене переменной в определенном интеграле. При одном условии – существование интеграла относительно новой переменной также должно гарантироваться.
Примеры.
1.
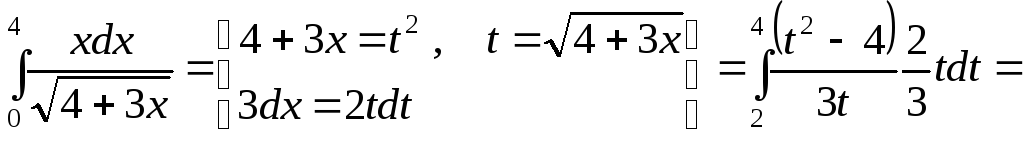
![]() .
.
Отметим, что при
осуществлении замены переменной в
соответствии с рекомендациями теории
необходимо эту замену уточнять, чтобы
не напутать при корректировке пределов.
В вычисленном интеграле теория рекомендует
замену
![]() ,
если корректировку пределов интегрирования
осуществлять с помощью этой формулы,
то
,
если корректировку пределов интегрирования
осуществлять с помощью этой формулы,
то![]() и
и![]() ,
,![]() и
и![]() .
Чтобы избежать путаницы в знаках, формулу
.
Чтобы избежать путаницы в знаках, формулу![]() следует записать либо в виде
следует записать либо в виде![]() ,
либо
,
либо![]() .
И тот, и другой варианты приводят к
желаемому результату – избавлению от
иррациональностей. Однако до установления
пределов интегрирования следует
остановиться на одной из формул. В
примере была выбрана первая формула.
.
И тот, и другой варианты приводят к
желаемому результату – избавлению от
иррациональностей. Однако до установления
пределов интегрирования следует
остановиться на одной из формул. В
примере была выбрана первая формула.
2.
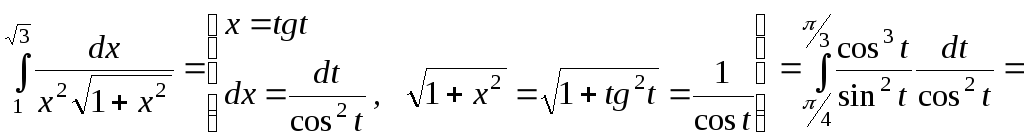
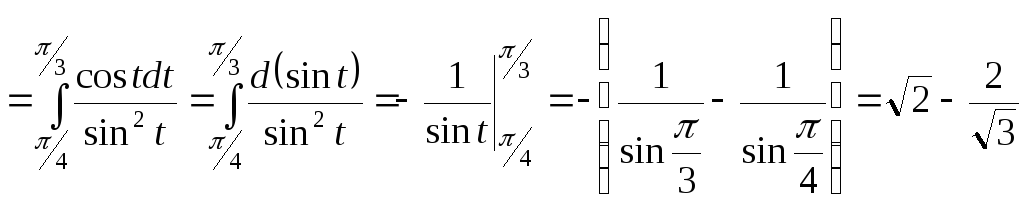 .
.
Для корректировки
пределов использовалась формула ![]() ,
из которой следует, что
,
из которой следует, что
![]() имеет место при
имеет место при![]() ,
а
,
а![]() реализуется при
реализуется при![]() .
.
Вычисление определенного интеграла с помощью максимы
В этом случае используется команда, мало отличающаяся от команды для вычисления неопределенного интеграла, лишь после переменной интегрирования добавляются пределы интегрирования, причем в порядке их возрастания.
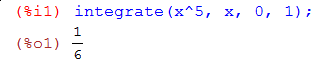
Например, команда
integrate(x^5,x,0,1)
и Shift+Enter
вычисляет интеграл ![]()
Интеграл
![]() ,
вычисленный ранее вручную,
,
вычисленный ранее вручную,

Интеграл ![]()
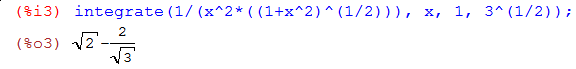
Примеры для самостоятельного решения
12.4.
![]() ,
12.5.
,
12.5.![]() , 12.6.
, 12.6.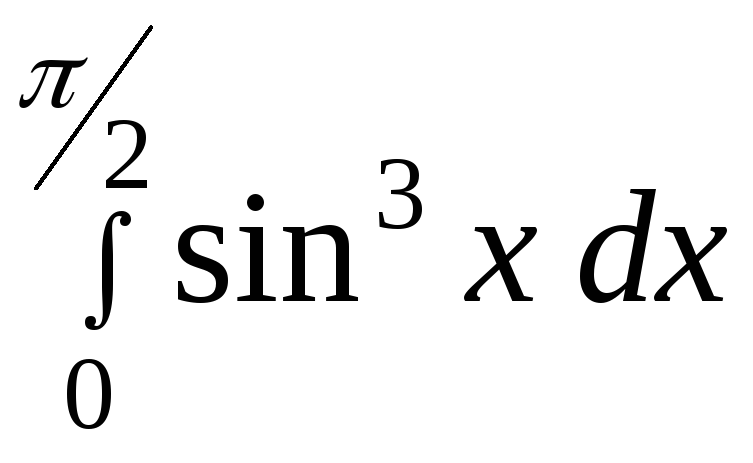 ,
,
12.7.
![]() ,
12.8.
,
12.8.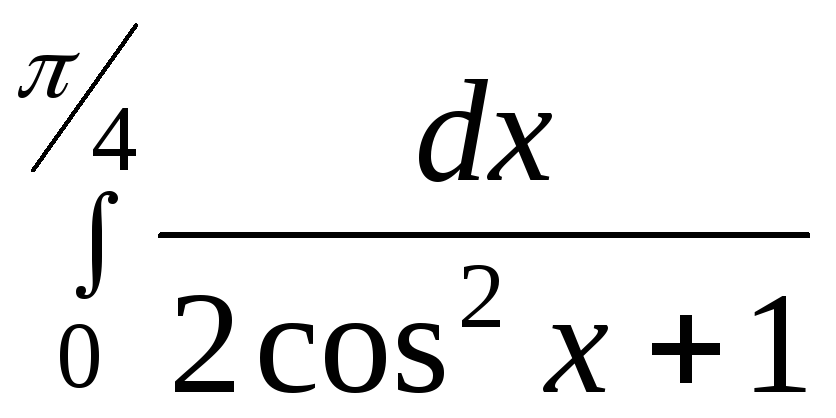 ,
12.9.
,
12.9.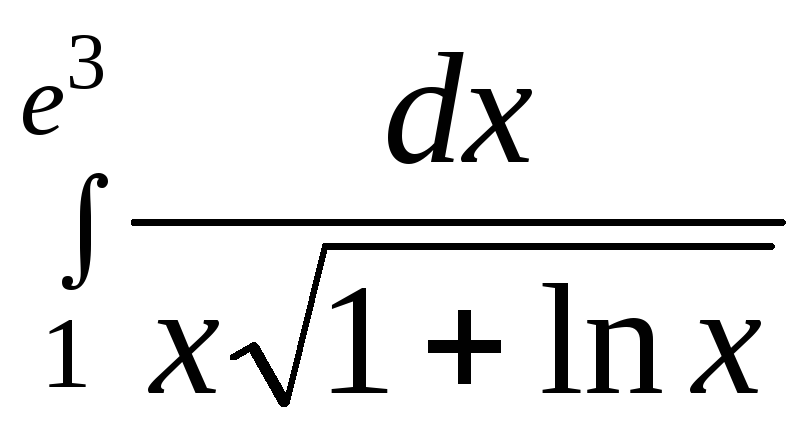 .
.
Ответы.
12.4.
![]() ,
12.5.
,
12.5.![]() ,
12.6.
,
12.6.![]() ,
12.7.
,
12.7.![]() ,
12.8.
,
12.8.![]() ,
12.9. 2.
,
12.9. 2.
Разные задачи
12.10.
![]() ,
12.11.
,
12.11.
![]() ,
,
12.12.
![]() ,
12.13.
,
12.13.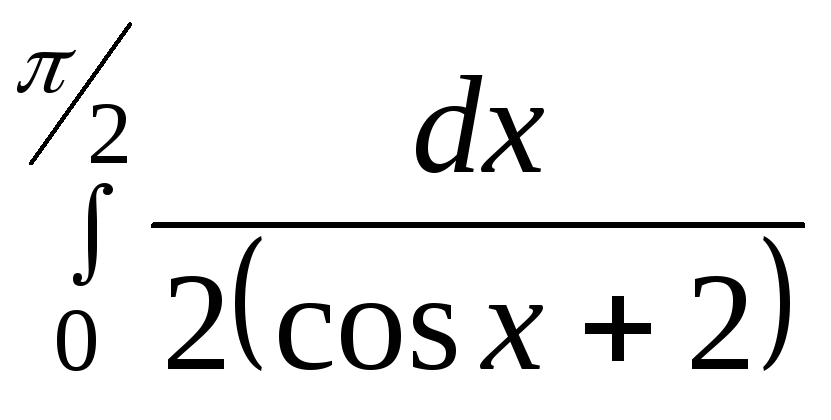 ,
,
12.14.
![]() ,
12.15.
,
12.15.
![]() ,
12.16.
,
12.16.
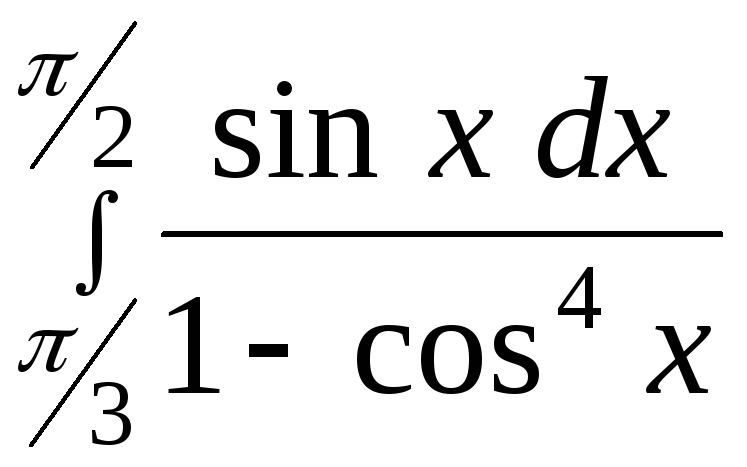 ,
,
12.17.
![]() ,
12.18.
,
12.18.
![]() ,
12.19.
,
12.19.
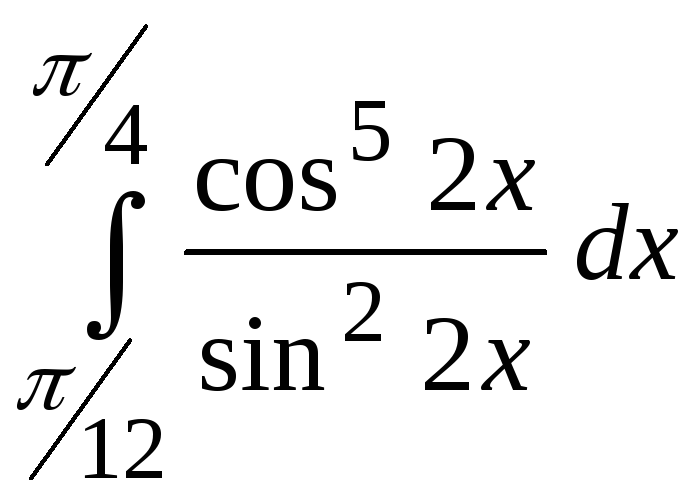 .
.
Ответы.
12.10. ![]() ,
12.11.
,
12.11. ![]() ,
12.12.
,
12.12. ![]() ,
12.13.
,
12.13. ![]() ,
,
12.14. ![]() ,
12.15.
,
12.15. ![]() ,
12.16.
,
12.16. ![]() ,
,
12.17. ![]() ,
12.18.
,
12.18.
![]() ,
12.19.
,
12.19.![]() .
.
Приложения определенного интеграла
Площадь фигуры
Декартова система координат
Выше было показано, что геометрический смысл определенного интеграла – площадь криволинейной трапеции. Покажем, как с его помощью определяются площади более сложных плоских фигур.
Явное задание функции
Поскольку значение
интеграла
![]() может быть как отрицательным, так и
положительным, а площадь фигуры –
величина положительная, следует
руководствоваться следующим правилом.
может быть как отрицательным, так и
положительным, а площадь фигуры –
величина положительная, следует
руководствоваться следующим правилом.
Если подынтегральная
функция на интервале
![]() меняет знак, скажем, в точках
меняет знак, скажем, в точках![]() и
и![]() ,
причем
,
причем![]() ,
площадь фигуры определяется формулой
,
площадь фигуры определяется формулой
![]() .
.
Покажем на примере
1, что может получиться, если не следовать
этому правилу. Пусть необходимо вычислить
площадь фигуры, ограниченной осью
абсцисс и кривой
![]() на интервале
на интервале![]() .
Если не заметить, что на этом интервале
синусоида меняет знак, проходя через
точку
.
Если не заметить, что на этом интервале
синусоида меняет знак, проходя через
точку![]() ,
то решение принимает вид
,
то решение принимает вид![]() .
Ясно, что получен неверный результат,
площадь этой фигуры не равна нулю. Теперь
применим вышеприведенную формулу
.
Ясно, что получен неверный результат,
площадь этой фигуры не равна нулю. Теперь
применим вышеприведенную формулу
![]() =2+2=4.
=2+2=4.
В рассмотренном примере ошибочное решение видно сразу, так как оно противоречит ожидаемому результату, но бывают случаи, когда ошибку в расчетах заметить трудно, а иногда и невозможно. Это происходит, когда площадь части фигуры, расположенной ниже оси абсцисс, скажем, значительно меньше площади части фигуры, расположенной в верхней полуплоскости. Тогда результат, полученный без разбиения интеграла на части будет не очень заметно отличаться от правильного результата. Эту ошибку без надлежащей проверки можно не заметить, хотя она может оказаться важной.
Пример 2. Вычислить площадь фигуры, ограниченной линиями
![]() .
.
Кривая пересекает
ось абсцисс при
![]() и
и![]() .
Очевидно, интересующая нас фигура
находится в области
.
Очевидно, интересующая нас фигура
находится в области![]() ,
причем подынтегральная функция в этой
области отрицательна (рисунок 41)
,
причем подынтегральная функция в этой
области отрицательна (рисунок 41)
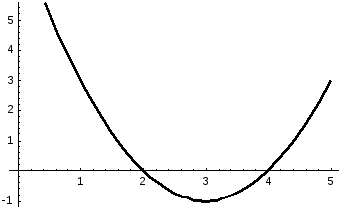
Рисунок 41.
![]() .
.

Пример 3. Вычислить
площадь фигуры, ограниченной линиями
![]() ,
,![]() ,
,![]()
![]() .
Сделаем рисунок
.
Сделаем рисунок
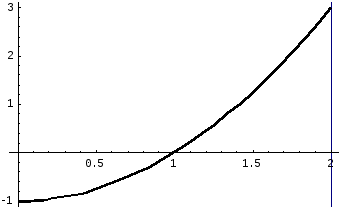
Рисунок 42.
Из рисунка 42 видно,
что часть фигуры расположена ниже оси
![]() ,
другая выше ее, причем кривая пересекает
ось абсцисс при
,
другая выше ее, причем кривая пересекает
ось абсцисс при![]() .
Итак,
.
Итак,
![]()
![]() .
.
![]()
Пример 4. Вычислить
площадь фигуры, находящейся в правой
полуплоскости
![]() и ограниченной линиями
и ограниченной линиями![]() ,
,![]() .
Сделаем рисунок
.
Сделаем рисунок
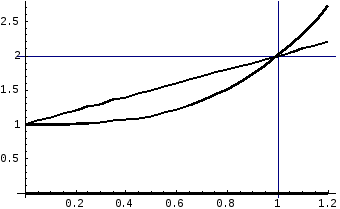
Рисунок 43.
Из рисунка 43
следует, что заданная фигура представляет
разность двух трапеций и занимает
область
![]() ,
формула ее площади имеет вид
,
формула ее площади имеет вид![]() ,
где
,
где![]() ,
,![]() .
Тогда
.
Тогда
![]() .
.

Параметрическое задание функции
Чтобы получить
формулу площади плоской фигуры, когда
уравнение кривой, ограничивающей фигуру,
задано параметрически
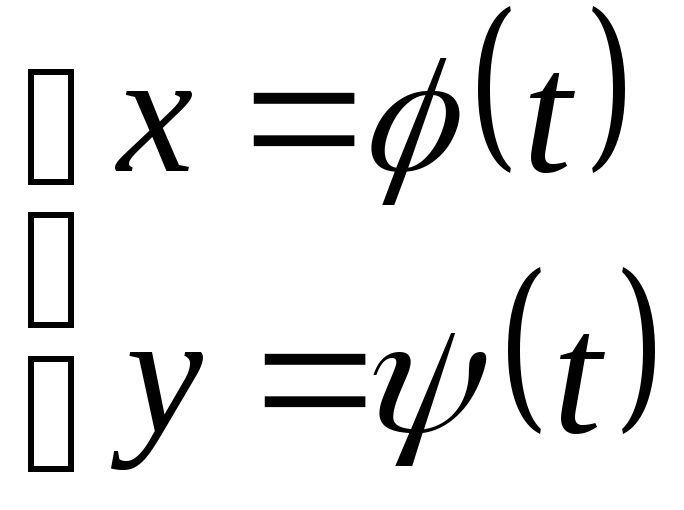 ,
следует в
,
следует в
формуле
![]() произвести замену переменной
произвести замену переменной
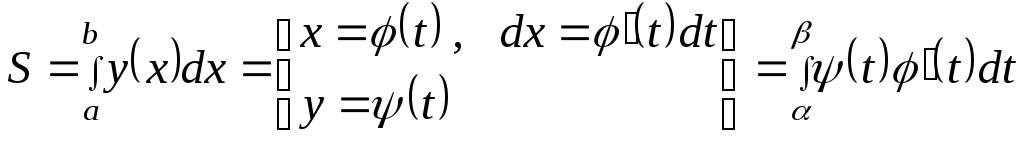 ,
,
здесь
![]() значение
переменной
значение
переменной![]() ,
соответствующее
,
соответствующее![]() ,
,![]() значение
переменной
значение
переменной![]() ,
соответствующее
,
соответствующее![]() .
Итак, для параметрически заданной
функции
.
Итак, для параметрически заданной
функции
![]() .
.
Здесь, как и в предыдущем параграфе, необходимо следить за точками, в которых функция меняет знак.
Пример 1. Вычислить
площадь фигуры, ограниченной одной
аркой циклоиды
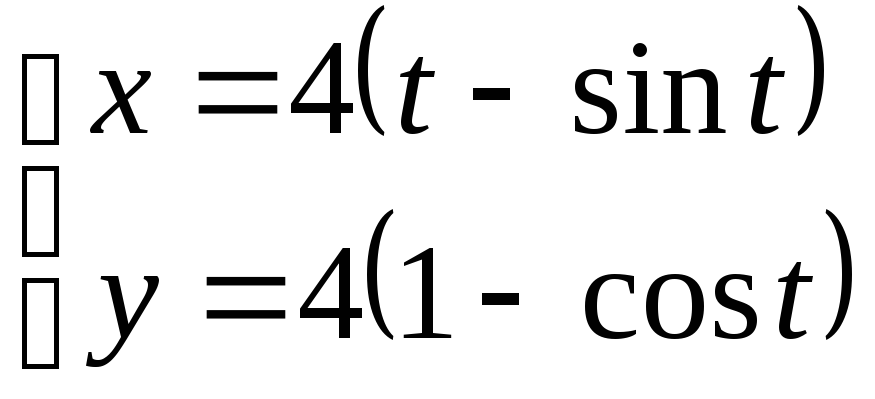 и осью абсцисс. Определим два ближайших
друг к другу значения параметра
и осью абсцисс. Определим два ближайших
друг к другу значения параметра![]() ,
при которых
,
при которых![]() .
Это
.
Это![]()
![]() и
и![]()
![]() .
Именно в этой области располагается
одна арка циклоиды, и в этих пределах
нужно производить интегрирование.
Сделаем рисунок
.
Именно в этой области располагается
одна арка циклоиды, и в этих пределах
нужно производить интегрирование.
Сделаем рисунок
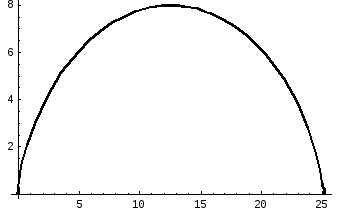
Рисунок 44.
Из рисунка видно,
что внутри области
![]() кривая знака не меняет. Тогда
кривая знака не меняет. Тогда
![]()
![]() .
.
Получим тот же результат с помощью МАКСИМЫ

Пример 2. Вычислить
площадь эллипса
![]() .
.
Запишем уравнение
эллипса в параметрической форме
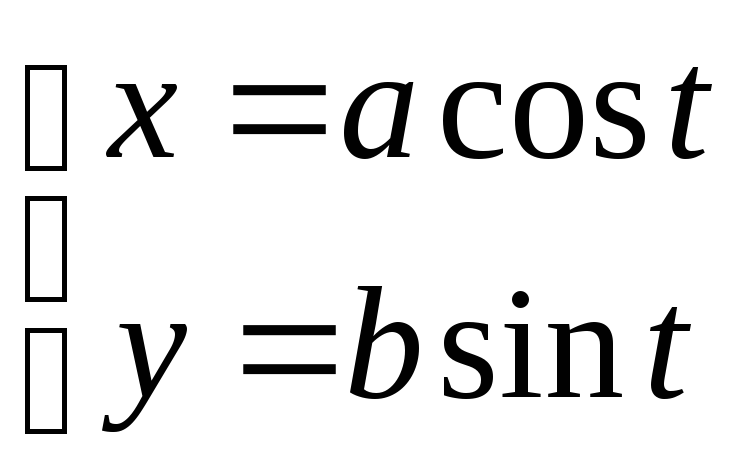 .
Если вычислить площадь фигуры,
расположенной в верхней полуплоскости
.
Если вычислить площадь фигуры,
расположенной в верхней полуплоскости![]() ,
полученный результат умножить на 2,
получим искомую площадь. Но эта часть
кривой реализуется при
,
полученный результат умножить на 2,
получим искомую площадь. Но эта часть
кривой реализуется при![]() .
Таким образом,
.
Таким образом,
![]()
![]() .
.
Полярная система координат
Определим площадь
криволинейного сектора, ограниченного
лучами
![]() ,
,![]() и кривой
и кривой![]() .
Разобьем область
.
Разобьем область![]() на
на![]() подобластей – элементарных секторов.
Заменим каждый элементарный сектор
сектором круга, радиус которого
подобластей – элементарных секторов.
Заменим каждый элементарный сектор
сектором круга, радиус которого![]() и угол
и угол![]() .
Тогда площадь элементарного сектора
равна
.
Тогда площадь элементарного сектора
равна![]() .
Площадь всего криволинейного сектора
приближенно описывается интегральной
суммой
.
Площадь всего криволинейного сектора
приближенно описывается интегральной
суммой![]() .
При этом с возрастанием числа разбиений
области
.
При этом с возрастанием числа разбиений
области![]() значение интегральной суммы приближается
к истинному значению площади криволинейного
сектора, так как уменьшается погрешность
замены каждого элементарного сектора
частью круга. Очевидно,
значение интегральной суммы приближается
к истинному значению площади криволинейного
сектора, так как уменьшается погрешность
замены каждого элементарного сектора
частью круга. Очевидно,![]() .
Однако, предел интегральной суммы, если
он не зависит от способа разбиения
области и выбора точек
.
Однако, предел интегральной суммы, если
он не зависит от способа разбиения
области и выбора точек![]() равен определенному интегралу.
Следовательно, площадь криволинейного
сектора определяется формулой
равен определенному интегралу.
Следовательно, площадь криволинейного
сектора определяется формулой
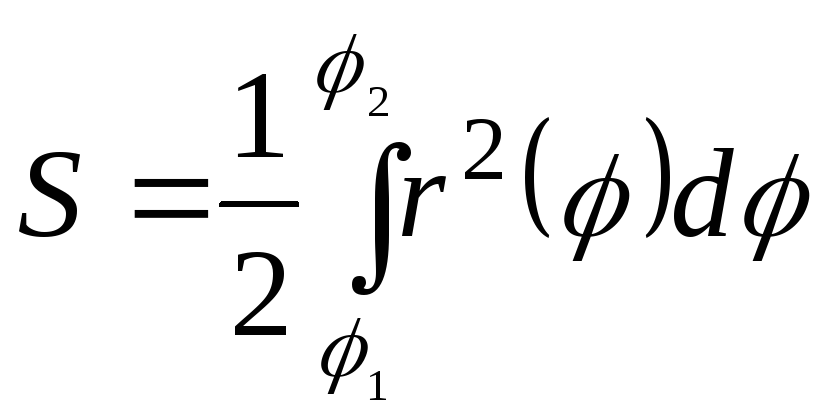 .
.
Пример 1. Вычислить
площадь фигуры, ограниченной одним
витком спирали Архимеда
![]() .
.

Рисунок 45.
Один виток спирали
проходится при изменении угла
![]() от 0 до
от 0 до![]() .
Тогда
.
Тогда![]() .
.

Пример 2. Вычислить
площадь фигуры, ограниченной кардиоидой
![]() .
Рисунок
.
Рисунок
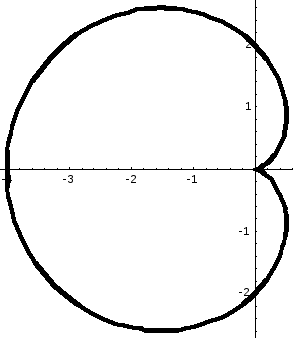
Рисунок 46.
Очевидно,
![]()
![]() .
.
