Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MAall

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

906.34 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Достаточность.

Пусть существует f0(x0). Тогда

f(x0 +

x) − f(x0)

= f0

(x0) + o(1),

x → 0. После умножения на

x + o(1) ·

x получаем: f(x0 + x) − f(x0) = f0(x0) ·

x → 0. Очевидно, o(1) ·

x = o(Δx), поэтому функция f(x) дифференцируема в точке

x0. Достаточность доказана. Теорема доказана.

Из доказательства теоремы видно, что число A в определении дифференцируемости

равно f0(x0).

В связи с этой теоремой функцию,

имеющую (конечную)

производную в

некоторой точке, называют дифференцируемой в этой точке.

Сам процесс вычисления

производной называют дифференцированием функции.

Теорема (о непрерывности дифференцируемой функции.) Если функция дифференци-

руема в некоторой точке, то она непрерывна в этой точке.

Доказательство.

Пусть

функция f(x) дифференцируема

в точке

x0.

То-

гда

f(x0 +

x) − f(x0)

f0(x0) ·

x + o(Δx),

→

Отсюда

lim f(x ) =

lim f(x +

f(x ) =

lim

(x )Δx + o(Δx)

= 0, т.е.

f(x )

при

x → 0. Это

−

f(x)

x = x0.

0 →

→

x 0

→

означает

что функция

непрерывна при

Теорема доказана

Достаточным условием дифференцируемости непрерывность не является. Мы видели,

что функция f(x) = |x| не имеет производной при x = 0. Однако, f(x) непрерывна в этой

√

точке (как и во всякой другой). Это следует, например, из равенства |x| = x2 и теоремы о непрерывности сложной функции. Можно доказать и непосредственно: если ε > 0, то, взяв

δ= ε, получим, что при |x−x0| < δ выполняются соотношения |x|−|x0| 6 |x−x0| < δ = ε,

т.е. |x| − |x0| < ε.

Рассмотрим теоремы о правилах дифференцирования функций.

Теорема (о производной суммы, произведения и частного.) Пусть функции f(x) и g(x) дифференцируемы в точке x0. Тогда в этой точке дифференцируемы также функции

f(x) ± g(x), f(x) · g(x),

f(x)

(последняя — при условии g(x) 6= 0), причём

g(x)

f(x) ± g(x0

) 0 = f0(x) ± g0(x)

f x)g(x) = f (x)g(x) + f(x)g (x)

f((x)

f0(x0)g(x)

−

f(x)g0(x0)

g(x)

Доказательство. Имеем:

f x

g x

)

0 =

lim

f(x +

g(x +

−

f(x)

g(x) =

( )

(

x 0

→

(

)

g x

)

g(x)

(

f0 x

lim

x −

x→0

( )

Производная произведения может быть вычислена так:

f(x)

g(x) 0

lim

f(x +

x)g(x +

x) − f(x)g(x)

x→0

−

f(x + x)g(x + x)

f(x)g(x + x) + f(x)g(x + x)

f(x)g(x)

= lim

x→0

f(x +

f(x)

g(x +

g(x)

lim

f x

−

) +

−

x→0

(

( )

= f0(x)g(x) + f(x)g0(x) .

Здесь мы воспользовались непрерывностью функции g(x), которая является следствием дифференцируемости: g(x + x) → g(x) при x → 0.

В случае производной частного рассуждаем аналогично

x→0

g(x + x)

− g(x)

f(x + x)

f(x)

lim

f(x + x) − f(x)

g(x)

−

f(x)

g(x + x) − g(x)

= lim

g(x) · g(x + x)

x→0

f0(x)g(x) − f(x)g0(x)

Теорема доказана.

g(x) 2

Пусть f(x) = C, где C — константа. Тогда

f0(x) = lim

f(x +

x) − f(x)

lim

C − C

= 0,

x→0

т.е. C0

0. Поскольку постоянный множитель можно вынести за знак предела, то

(Cf(x))0 = Cf0(x).

Теорема (о производной сложной функции).

Пусть функции f(x) и g(y) опреде-

лены в окрестностях соответственно точек x0 и y0 и дифференцируемы в этих точ-

ках, y0

= f(x0).

Тогда сложная

функция g(f(x))

дифференцируема

в точке x0,

g(f(x)) 0

= g0(y0) f0(x0).

x=x0

Функция

дифференцируема

следовательно

непре

Доказательство

f(x)

рывна

в точке

x0.

Пусть функция

g(y) определена

для

тех

для

которых

|y − y0| <

ε.

Тогда существует

такое,

что при |x −

x0| < δ

выполняется неравенство |f(x)

− f(x0)|

|f(x) − y0|

ε,

для

таких

имеет смысл

сложная

функция g(f(x)).

Таким образом, сложная функция g(f(x))

определена в окрестности точки x0, и

можно говорить о её производной в этой

точке.

Запишем

определение

дифференцируемости

функции

g(y)

точке

y0:

g(y0 + y) − g(y0) = g0(y0)Δy + o(Δy) ,

y → 0.

o(Δy)

Пусть α(Δy) =

, если

и α(Δy) =

0, если

Очевидно,

α(Δy) → 0,

если

y → 0. Определение дифференцируемости можно переписать так:

g(y0 + y) − g(y0) = g0(y0)Δy + α(Δy) · y,

y → 0.

При достаточно малом

x подставим сюда y0 = f(x0),

y = f(x0 + x) − f(x0). Тогда

g f(x0 + x) − g f(x0) = g0(y0) f(x0 + x) − f(x0) + α(Δy) f(x0 + x) − f(x0) .

Отсюда

g(f(x)) 0

lim

g f(x0 +

− g f(x0)

x=x0

→

f(x0 + x)

f(x0)

= lim

(y0)

−

x→0

f(x0 + x)

f(x0)

+ lim

α(f(x

f(x

)

. (1)

−

x −

x→0

Заметим, что α(f(x0 +

x) − f(x0)) → 0, т.к.

f(x0 +

x) − f(x0) → 0 при

x → 0 —

дифференцируемая в точке x0 функция f(x) непрерывна в этой точке.

Кроме того,

f(x0 +

x) − f(x0)

→

f0(x

) при

→

Поэтому последний предел в (1) равен нулю, и

мы получаем требуемое равенство:

x=x0 = g0(y0) · f0(x0) .

g(f(x)) 0

Теорема доказана.

Правило дифференцирования сложной функции часто записывают в виде

g(f(x)) 0 = g0(f(x)) · f0(x) ,

где под g0 f(x) понимается производная функции g(y), вычисленная при y = f(x).

Теорема (о производной обратной функции.) Пусть функция f(x) осуществляет вза-

имно однозначное отображение окрестности U(x0) точки x0 на окрестность V (y0) точки y0 = f(x0), причём обратная функция f−1(y) непрерывна в точке y0. Тогда, если существует f0(x0) 6= 0, то существует также и (f−1)0(y0), причём

(f−1)0(y0) =

(x0)

Доказательство.

Пусть y0 + y V (y0), и пусть f−1(y0 +

y) = x0 +

x. Далее,

f−1(y0) = x0, и

f−1(y0 +

y) − f−1(y0) = x0 +

x − x0 =

x ,

(2)

f(x0 + x) − f(x0) = f(f−1(y0 + y)) − y0 = y0 + y − y0 = y .

Если y 6= 0 то и

x 6= 0 — это вытекает из того, что отображение f: U(x0) → V (y0)

взаимно однозначно.

Заметим ещё, что из непрерывности функции f−1(y) в точке y0 и

из (2) следует, что если y → 0, то и

x → 0.

Теперь можно вычислить производную

обратной функции:

(f−1)0(y0) = lim

f−1(y0 + y) − f−1(y0)

lim

f−1

(y0

+ y) − f−1

(y0)

→

y 0

= lim

(

0 +

x −

→

)

f0(x0)

f(x

Теорема доказана.

Пример. Функция f(x) = x2 взаимно однозначно отображает бесконечный интервал (0, +∞) на себя. Поэтому существует обратная функция f−1(y) = √y, которая непрерывна по теореме о непрерывности обратной функции. Вычислим производную функции f(x):

f0(x) = lim	(x +	x)2 − x2	=	lim	x2 + 2x	x +	x2 − x2	=

		x				x
x→0				x→0

= lim (2x + x) = 2x.

x→0

Мы видим, что f0(x) 6= 0 на интервале (0, +∞). Поэтому обратная функция дифференцируема в каждой точке такого интервала. Для её производной имеем:

(f−1)0(y) = (√		)0 =	1		21x	x=√y=	1
(f−1)0(y) = (√	y	)0 =	f0(f−1(y))	=	21x	x=√y=	2√y .

√ 0 1

Таким образом, ( y) = 2√y .

кафедра «Математическое моделирование» проф. П. Л. Иванков

Математический анализ

конспект лекций

для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)

Лекция 12.

Таблица производных элементарных функций. Логарифмическая производная и ее применение. Производные высших порядков. Механический смысл второй производной. Дифференциал функции, его геометрический смысл. Правила вычисления дифференциалов. Инвариантность формы первого дифференциала. Применение дифференциалов к приближенным вычислениям. Дифференциалы высших порядков. Дифференцирование неявно и параметрически заданных функций (первая и вторая производная).

ОЛ-2, пп. 1.7, 2.2-2.4, гл. 3.

Найдём производные основных элементарных функций. Если y = ex, то

y0(x) = (ex)0

= lim

ex+Δx − ex

= ex

lim

e x − 1

x→0

Пусть x = ln(1 + t); тогда t → 0 при

x → 0, и мы получаем

y0(x) = ex lim

x − 1

= ex lim

eln(1+t) − 1

= ex lim

ln(1 + t)

ln(1 + t)1/t

x→0

t→0

= e

t→0

= e

ln e

= e ,

lim(1 + t)1/t

т.к. по теореме о втором замечательном пределе (1+ прерывна в точке x = e. Если a > 0, a 6= 1, то ax = ex сложной функции

t)1/t → e при t → 0, и функция ln x не- ln a, и по правилу дифференцирования

(ax)0 = (ex ln a)0 = ex ln a ln a = ax ln a.

Производную логарифмической функции найдём, используя правило дифференци-

рования

обратной

функции.

Действительно,

loga x,

> 0,

a 6= 1, являются взаимно

обратными

функциями.

Поэтому

при

имеем

(loga x)0

. Если a = e, то получаем отсюда формулу

(ay)0|y=loga x

(ln x)0 =

aloga x ln a

x ln a

Для

функции

xα

при

имеем

(используем

степенной

правило

дифференцирования

сложной

функции

полученные

выше

результаты):

(xα)0 = (eα ln x)0 = eα ln x · αx = αxxα = αxα−1, т.е. (xα)0 = αxα−1. Эта же формула остается

в силе и в точке x = 0 (для α > 1; если соответствующая степенная функция определена лишь при x > 0, то эта формула даёт значение правой производной). В самом деле, если

α > 1, то (считаем, что

x > 0, если функция y = xα не определена при x < 0):

(xα)0

x=0

lim

(Δx)α

если α = 1,

если

α > 1,

x→0

т.е.

(xα)0|x=0 = αxα−1|x=0. Если же x отрицательно, и функция y = xα определена при

таких x, то эта функция является либо чётной либо нечётной, т.е.

при x < 0 имеем

xα = ±(−x)α. Тогда

± (−x)α

xα

(xα)0 =

(

x)α

α( x)α−1

(

x)0

= α

( 1) = α

= α xα−1 ,

и (x

)0 = α x

α±1

−

−x

· −

− также и при x < 0.

Рассмотрим тригонометрические функции. Имеем

sin(x +

x) − sin x

2 sin

· cos x +

(sin x)0 =

lim

= lim

x→0

sin

lim

· cos

= cos

x .

x→0

Мы

воспользовались

теоремой

первом

замечательном пределе

непре-

рывностью

функцииπ

cos x.

Далее,

π cos0

sinπ x +

поэтому

(cos x)0

sin

x +

cos

x +

cos

x +

− sin x, т.е.

(cos

= −

sin x.

Производные тангенса и котангенса найдём по правилу дифференцирования дроби:

sin x

cos2 x + sin2 x

(tg x)0 =

cos x

cos2 x

cos x

sin2 x

cos2 x

(ctg x)0

−

= −

sin x

sin2 x

Таким образом, (tg x)0

, (ctg x)0 = −

cos2 x

sin2 x

Рассмотрим обратные тригонометрические функции. Функция y = sin x дифференци-

(sin x)0 = cos x.

y = arcsin x

1 < x < 1

руема на интервале

−

и имеет на этом интервале отличную от нуля производную

Поэтому для обратной функции

при

−

имеем

(arcsin x)0 =

√

cos y

cos(arcsin x)

y=arcsin x

p1 −

sin

(arcsin x)

1 − x

√1 − x2

−

т.е. (arcsin x)0

В формуле

cos(arcsin x) = √1

x2 мы взяли знак «+» перед

радикалом потому, что arcsin x

−

, и косинус положителен на этом интервале.

Аналогично вычисляется и

производная арккосинуса

Функция

y = cos x

на интервале

(0, π) имеет отличную от нуля производную (cos x)0 = − sin x, поэтому

(arccos x)0 =

= −

− sin y y=arccos x

sin(arccos x)

1 − cos2(arccos x)

= −√

1 − x2

если

(−1

, 1).

Можно

также

воспользоваться соотношением

известным

из

элементарной

тригонометрии.

Имеем

arccos x +

arcsin x

Выбор знака «

» перед радикалом в ис

(arccos x)0

− arcsin x

= −√

1 − x2

пользованной выше формуле sin(arccos x) =

√

объясняется тем, что arccos x (0, π),

1 − x

и функция y

= sin x положительна на этом интервале.

Заметим, что рассмотренные

функции y =

arcsin x и y =

arccos x не имеют конечной производной при x ± 1. Для

функции y = arctg x имеем

(arctg x)0

= cos2(arctg x) =

(tg y)0 y=arctg x

1/ cos2(arctg x)

1 + tg2(arctg x)

1 + x2

т.е. (arctg x)0

. Аналогично,

1 + x2

(arcctg x)0 =

= −

= − sin2(arcctg x) =

(ctg y)0 y=arcctg x

1/ sin2(arcctg x)

= −

1 + ctg2(arcctg x)

1 + x2

Этот

же

результат

можно

получить быстрее, если воспользоваться равенством

arcctg x + arctg x =

и предыдущей формулой.

Производные гиперболических функций можно вычислить с помощью формул (ex)0 = ex

и (e−x)0 =

−

e−x.

Например, (sh x)0 =

− e−x

ex + e−x

= сh x.

Аналогично

(сh x)0

= sh x, (th x)0

, (cth x)0 = −

сh2 x

sh2 x

Составим таблицу производных основных элементарных функций.

1.	(ax)0 = ax ln a, (ex)0 = ex .
2.	(loga x)0 =					1			,				(ln x)0						=	1		.
2.	(loga x)0 =								,				(ln x)0						=			.
				x ln a																x
3.	(xα)0 = αxα−1 , (√															)0 =			1		,
													x						1
													x
	(cos x)0	= − sin x.																	2√x
4.	(cos x)0	= − sin x.
5.	(sin x)0	= cos x .
6.	(tg x)0 =			1			.

			cos2 x
7.	(ctg x)0	= −				1					.

					sin2 x
8.	(arcsin x)0			=		1								.


						√1 − x2
9.	(arccos x)0			= −√						1								.
9.	(arccos x)0			= −√						1 − x							2	.
	(arctg x)0 =					1				1 − x
10.						1						.

						1 + x2
	(arcctg x)0					1
11.				= −											.
11.				= −				1 + x2							.

1 0 = − 1 . x x2

Эту таблицу полезно дополнить формулами:
12.	C0 = 0 — производная константы равна нулю .
13. (сh x)0 = sh x .
14.	(sh x)0	= сh x .
15.	(th x)0	=	1		.

			сh2 x
			1
16.	(cth x)0 = −					.
				sh2 x

Рекомендуется также запомнить производные некоторых часто встречающихся функций.

Например, (√

)0 =

1 + x2

√1 + x2

Пусть функция y = f(x) дифференцируема и отлична от нуля на некотором про-

межутке I. Тогда в точках этого промежутка определена

функция

ln |f(x)|.

Найдём

производную

этой

функции. Пусть сначала

f(x)

для

всех

Тогда

ln f(x) 0

f0(x)

Если

f(x)

при

всех

то

(x)

f(f)0(x)

f0(x)

f(x)

ln(

−

f(x)) 0

−

, т.е.

в обоих случаях

ln f(x)

−f(x)

f(x)

Производная от логарифма

(

модуля

функции называется логарифмической производной

)

Eсли последнюю формулу переписать в виде f0(x) = f(x)·(ln |f(x)|)0, то её можно использовать для вычисления f0(x) в тех случаях, когда логарифмическую производную вычислить проще, чем производную самой функции.

	Пример. Пусть y = (f(x))g(x). Тогда
	= y(ln y)0 = y (g(x) · ln f(x))0 = g0(x) · ln f(x) + g(x) ·	f (x)		·		g(x)
y0		0			f(x)		.
y0		f(x)			f(x)		.
	Если функция f(x) дифференцируема в каждой точке		промежутка				то на этом про	-
	Если функция f(x) дифференцируема в каждой точке					I,		-

межутке определена функция f0(x), для которой также можно рассмотреть вопрос о её производной в точках промежутка I. Если такая производная в точке x существует, то она называется второй производной исходной функции f(x) и обозначается f00(x). Производная рассматириваемой функции n-го порядка определяется по индукции. пусть x I, и пусть в окрестности этой точки определена производная (n − 1)-го порядка f(n−1)(x). Тогда производная n-го порядка f(n)(x) в точке x по определению есть f(n−1)(x) 0. Таким образом, в соответствии с этим определением для существования f(n)(x) в точке x требуется, чтобы в некоторой окрестности этой точки существовали производные f(k)(x), k = 0, 1, . . . , n − 1, и чтобы производная (n − 1)-го порядка f(n−1)(x) была дифференцируема в т. x (при этом под «производной нулевого порядка» здесь и далее понимается сама функция f(x)).

Пусть материальная точка движется вдоль ось абсцисс, и пусть зависимость её координаты от времени определяется равенством x = x(t). Тогда мгновенная скорость изменения координаты (в данном случае абсциссы) материальной точки равна, как известно, v(t) = x0(t). Для характеристики скорости изменения v(t) с течением времени вводят

понятие ускорения материальной точки:

a(t) = lim

v(t +

v(t)

lim

x0(t +

x0(t)

= x00(t) ,

−

t→0

т.е. ускорение есть вторая производная координаты по времени. В этом состоит механический смысл второй производной.

Вычислим производные n-го порядка некоторых элементарных функций. Пусть сначала y = ax. В этом случае y0 = ax ln a, y00 = ax ln2 a и т.д. Общая формула y(n) = ax lnn a

доказывается по индукции. В частности, при a = e имеем (ex)(n) = ex, n = 0, 1, 2, . . . .

Рассмотрим степенную функцию y = xα. Здесь y0 = α xα−1, y00 = α (α − 1) xα−2 и т.д. Общая формула (xα)(n) = α (α − 1) . . . (α − n + 1) xα−n доказывается по индукции. Для логарифмической функции y = loga x можно воспользоваться этим результатом при α = −1. Имеем

y0 =

, y00 =

−1

, y000 =

, yIV =

2 · 3

, yV

2 · 3 · 4

и т.д.

x ln a

x2 ln a

x3 ln a

−x4 ln a

x5 ln a

Нетрудно угадать общую формулу

y(n) =

(−1)n−1(n − 1)!

(1)

xn ln a

При n = 1, 2, 3, 4, 5 эта формула справедлива. Для производной (n + 1)-го порядка имеем

( 1)n−1(n

1)!

(

−

1)n−1(n

1)!(

( 1)nn!

xn ln a

xn+1 ln a

y(n+1) = (y(n))0 =

−

и по индукции формула (1) доказана.

Пусть y = sin x. Докажем, что

(sin x)(n) = sin x + n

(2)

При n = 0 имеем (sin x)(0) = sin x = sin

x + 0 ·

. Пусть при некотором n формула (2)

справедлива. Тогда

sin x + n

= cos x + n 2

= sin x + n 2

+ 2

= π

(sin x)(n+1) = (sin x)(n) 0

= sin x + (n + 1)

и формула (2) доказана.

Аналогично доказывается и правило вычисления производной

n-го порядка косинуса:

(cos x)(n) = cos x + n

Рассмотрим еще формулу Лейбница

(u v)(n) = k=0 k u(n−k) v(k),

где для краткости у функций u = u(x) и v = v(x) не указана зависимость от x.

Обе

эти функции предполагаются дифференцируемыми соответствующее число раз в точке

x. Для доказательства формулы

Лейбница применим индукцию

При

n = 1

формула

справедлива

т к

(u v) = u v + u v

v +

. Пусть при некотором n формула

Лейбница уже,

доказана. . 0. Тогда0

(u v)(n+1) =

(u v)(n)) 0 =

u(n−k) v(k)!

k=0

u(n+1−k) v(k)+

= k=0 k

u(n+1−k) v(k)

+ u(n−k) v(k+1) = u(n+1) v(0) + k=1

n−1	n	u(n−k) v(k+1) + u(0) v(n+1) = u(n+1) v(0)+
+ k=0	k	u(n−k) v(k+1) + u(0) v(n+1) = u(n+1) v(0)+
n X		+	k 1	u(n+1−k) v(k) + u(0) v(n+1)		=
+ k=1 k		+	k 1	u(n+1−k) v(k) + u(0) v(n+1)		=
X	n		n
X			−	n+1			u(n+1−k) v(k).
				= k=0		k	u(n+1−k) v(k).
				X	n + 1
				X

Доказательство вполне аналогично доказательству формулы бинома Ньютона; на заключительном этапе рассуждения мы воспользовались равенствами

k	+	k − 1	=	k	,
n		n		n + 1	u(n+1−0) v(0) и u(0) v(n+1) =	n + 1	u(n+1−n−1) v(n+1).
		u(n+1) v(0) =		0	u(n+1−0) v(0) и u(0) v(n+1) =	n + 1	u(n+1−n−1) v(n+1).
				n + 1		n + 1

По индукции формула Лейбница доказана. Рассмотрим вопрос о дифференцировании функции, заданной параметрически. Пусть

на интервале (t1, t2) заданы две функции
x = x(t) и y = y(t) ,	(3)

причём первая их них осуществляет взаимно однозначное отображение интервала (t1, t2) на интервал (x1, x2). В таком случае определена обратная функция t = t(x), и на интервале (x1, x2) можно рассмотреть сложную функцию y(x) = y(t(x)). Про эту последнюю функцию говорят, что она задана параметрически равенствами (3). Предположим, что выполнены условия, при которых применимы правила дифференцирования сложной и обратной функций, и в этом предположении вычислим производную y0(x); имеем

y0(x) = y(t(x)) 0 = y0(t(x)) · t0

y0(t(x))

, т.е. y0(x) =

y0(t(x))

(x) =

x0(t(x))

Обычно эту формулу записывают короче: y0(x) =

y0(t)

√

x0(t)

√

Пример

Пусть

Здесь

t, t

(0, +∞).

y(x) = p

√

√4

x(t) = t , y(t) =

t(x) =

. Производная этой функции по доказанной формуле

y (t)

(x) = x00(t) =

2√t

· 2t

t=√x = 4x3/4

= 4√4 x3 .

Рассмотрим равенство

F (x, y) = 0 ,

(4)

где F (x, y) — «функция двух переменных». Можно считать, что левая часть (4) — это некоторая формула, содержащая x и y. Если для функции y = y(x), заданной на промежутке I, для всех x из этого промежутка выполняется равенство F (x, y(x)) = 0, то говорят, что функция y = y(x) задана неявно равенством (4). Чтобы найти производную функции, заданной неявно, надо продифференцировать равенство F (x, y(x)) = 0 по x, используя

правило дифференцирования сложной функции. Из получившегося соотношения между x, y(x) и y0(x) можно затем выразить y0(x) через x и y(x).

	Пример.		Пусть x2 + y2 = 1. Тогда, если x2 + (y(x))2 = 1, то 2x + 2y(x) · y0(x) = 0, и
		x	√			x
				2
y0	(x) = −		. Например, если y(x) =	1 − x	, то y0(x) = −√			.
		y(x)
						1 − x	2

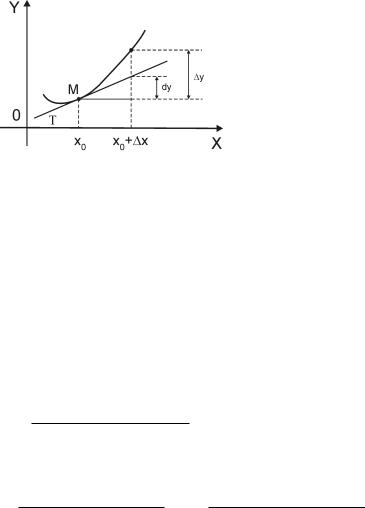
Пусть функция y = f(x) дифференцируема в точке x. Тогда приращение этой функции может быть записано в виде

y = f(x + x) − f(x) = f0(x)Δx + o(Δx) , x → 0 .

Дифференциалом df(x) функции f(x) в точке x называется f0(x)Δx. Эта часть прираще-


ния y = f(x+	x)	−	f(x) линейна относительно x, а при f0		6
					(x) = 0 она является главной
частью y при	x → 0. Приращение			x независимой переменной называется дифферен-

циалом независимой переменной и обозначается dx. В таком случае df(x) = f0(x)dx, и

f0(x) =	df(x)	. Правую часть этого равенства используют также для обозначения произ-

	dx			df(x)
водной; при этом					следует рассматривать не как дробь, а как единое выражение.

				dx
Примеры.			Имеем по определению dex = exdx, d xα = α xα−1dx, d ln x =			1	dx,

						x

d cos x = − sin x dx и т.д.

Рассмотрим геометрический смысл дифференциала. Уравнение касательной T к графику функции y = f(x) в точке M(x0, f(x0)) есть y = f(x0) + f0(x0)(x − x0). Очевидно, ордината касательной при x = x0 равна f(x0). При x = x0 + x ордината касательной T равна f(x0) + f0(x0)Δx. Приращение ординаты касательной, следовательно, равно f0(x0)Δx, т.е. равно дифференциалу функции f(x) в точке x0, отвечающему приращению

x независимой переменной. В этом состоит геометрический смысл дифференциала. Поскольку дифференциал равен производной функции, умноженной на дифференциал

независимой переменной, то правила вычисления дифференциалов мало чем отличаются от соответствующих правил вычисления производных. Например,

d(f(x) + g(x)) = df(x) + dg(x) ,

d(f(x) · g(x)) = df(x) · g(x) + f(x) · dg(x) ,

f(x)

g(x) df(x) − f(x) dg(x)

g(x)

(g(x))2

Докажем лишь последнее равенство. Имеем

f(x)

0 dx =

f0(x)g(x) − f(x)g0(x)

dx =

g(x) df(x) − f(x) dg(x)

g(x)

(g(x))2

Пусть функция f(x) дифференцируема в точке x. Тогда

df(x) = f0(x) dx .

(1)

Рассмотрим теперь сложную функцию f(x(t)). Дифференциал этой функции можно найти с помощью правила дифференцирования сложной функции: df(x(t)) = f0(x(t)) x0(t) dt. Поскольку x0(t) dt = dx(t), то имеем также равенство df(x(t)) = f0(x(t)) dx(t). Если не указывать здесь зависимость от t, то мы вернёмся к прежней форме (1) записи дифференциала:

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.20156.04 Mб21m07.pdf
#
10.02.2015291.36 Кб61m1.pdf
#
21.04.2015312.58 Кб16m101.pdf
#
12.03.2015615.2 Кб29m107.pdf
#
09.02.2015979.24 Кб10MA3.pdf
#
10.02.2015906.34 Кб10MAall.pdf
#
09.02.2015862.2 Кб16MAall.pdf
#
10.02.2015909.4 Кб5MAiu9.pdf
#
09.02.2015160.26 Кб9maket ОФОРМЛЕНИЕ ДОКЛАДОВ.doc
#
21.12.2018553.47 Кб2Management.doc
#
10.02.20151.54 Mб84Manual for the Matlab toolbox EKFUKF.pdf