
MAall
.pdf
при всех n > N1. |
|
Пусть задано |
|
ε > 0. |
|
Тогда для положительного числа |
ε|b|2 |
|
||||||||||||||||||||
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
| |
|
n − |
|
| |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
существует номер N |
|
такой, что при |
n |
|
N |
|
справедливо неравенство |
|
y |
|
b |
|
< |
ε|b|2 |
. |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
При n > max(N1, N2) имеем тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
1 |
|
|
|
|
y |
|
b |
|
2 |
|
|
ε b |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
− |
|
= |
|
| n − | |
|
< |
|
|
· |
| | |
|
= ε, |
|
|
|
|
|
|
|
|
|||||
|
|
b |
yn |
b yn |
|
b |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
| |
| · | |
| |
|
| | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. |
|
1 |
1 |
|
< ε, |
если n |
> max(N1, N2). Поэтому |
nlim |
1 |
1 |
а отсюда, как |
|||||
b − y |
|
y |
= b , |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
→∞ n |
|
|
|
|
|||
отмечалось |
выше |
, вытекает справедливость теоремы. Теорема доказана. |
|
|||||||||||||
Последовательность {xn} |
называется фундаментальной, если для любого ε > 0 |
|||||||||||||||
существует номер |
N = N(ε) |
такой, что при любых m > N |
и |
n > N |
выполняется |
|||||||||||
неравенство |xm − xn| < ε. |
|
|
|
|
|
|
|
|||||||||
Следующая теорема является основной в теории пределов. |
|
|
|
|
|
|||||||||||
Теорема (Критерий Коши существования предела последовательности). Для того,
чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
Поскольку в этой теореме идет речь об эквивалентности двух условий, то ее доказательство естественным образом распадается на две части: доказательство необходимости
и доказательство достаточности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство необходимости. |
Требуется доказать, что если последовательность |
|||||||||||||||||
сходится, то она фундаментальна. |
Пусть |
{xn} — |
сходящаяся |
последовательность |
, |
|||||||||||||
|
ε |
|
||||||||||||||||
a = |
lim xn, и пусть задано ε > 0. |
Для положительного числа |
|
|
|
|
найдется номер |
|||||||||||
2 |
||||||||||||||||||
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
N такой, что при m > N и n > N выполняются |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
неравенства |
|
ε |
|
|
|
ε |
|
|
|
|
|
|
|
|||||
|
|a − xm| |
|
и |
|a − xn| < |
|
|
|
|
|
|
|
|
||||||
|
< |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
2 |
2 |
|
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
ε |
|
|
|
ε |
|
|
||||
|
|xm − xn| = |(xm − a) + (a − xn)| 6 |xm − a| + |a − xn| < |
|
|
|
|
|
||||||||||||
|
|
|
+ |
|
= ε, |
|
|
|||||||||||
|
2 |
2 |
|
|
||||||||||||||
т.е. |
|xm − xn| < ε, если m > N и n > N. Мы видим, что последовательность {xn} |
|
||||||||||||||||
фундаментальна. Необходимость доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство достаточности. |
Здесь требуется доказать, что если |
{xn} — |
||||||||||||||||
фундаментальная последовательность, то у этой последовательности существует предел. Докажем сначала, что {xn} ограничена. Для положительного числа 1 существует номер
Nтакой, что при m > N и n > N выполняется неравенство |xm − xn| < 1. В
частности, при m = N отсюда следует, что при всех n > N справедливо неравенство
|xN − xn| < 1. Следовательно, |
|xn| − |xN | 6 |xN − xn| < 1, и |xn| 6 |xN | + 1. Поэтому при |
|||||||||||||||||||||||||||
всех n = 1, 2, . . . имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|xn| 6 max(|x1|, . . . , |xN |, |
|xN | + 1), |
|
|
|
|
||||||||||||||||||||
и последовательность {xn} ограничена. |
|
Поэтому все элементы этой последовательно- |
||||||||||||||||||||||||||
сти принадлежат некоторому отрезку |
[a1, b1]. |
Разделим этот отрезок пополам и из двух |
||||||||||||||||||||||||||
образовавшихся отрезков |
a1, |
|
a |
1 |
+ b |
1 |
и |
|
a |
1 |
+ b |
1 |
, |
|
b1 |
|
выберем тот, который содержит |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||
бесконечно много элементов рассматриваемой последовательности |
{xn}. Обозначим вы- |
|||||||||||||||||||||||||||
бранный отрезок [a |
, b |
]. Очевидно, |
[a |
, b |
] |
|
[a |
, b |
] |
и b |
2 − |
a |
|
= |
b1 − a1 |
. Далее разделим |
||||||||||||
2 |
2 |
|
|
|
|
|
|
|
1 |
1 |
|
2 |
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|||||
4

|
|
|
|
|
|
|
a |
+ b |
2 |
|
|
|
a |
2 |
+ b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
[a2, b2] пополам и из двух отрезков |
a2, |
|
|
2 |
|
|
и |
|
|
|
|
|
, b2 |
|
|
выберем тот, который |
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||
содержит бесконечно много элементов последовательности |
{xn}. |
Вновь выбранный отре- |
||||||||||||||||||||||||||||||
зок обозначим [a |
, b |
]. Очевидно, |
[a |
, b |
] |
|
[a |
, b |
] |
|
[a |
, b |
], |
|
и b |
|
− |
a |
|
= |
b2 − a2 |
= |
b1 − a1 |
. |
||||||||
3 |
3 |
|
1 |
1 |
|
2 |
|
2 |
|
3 |
|
|
3 |
|
|
|
|
3 |
|
3 |
2 |
4 |
|
|||||||||
Продолжая этот процесс выбора отрезков, получим последовательность вложенных отрез-
ков [a |
, b |
] |
|
[a |
, b |
] |
|
. . . |
|
[a |
|
, b |
|
] |
|
. . . , причем |
b |
n − |
a |
|
= |
b1 − a1 |
. |
По лемме о |
||||||
1 |
1 |
|
2 |
2 |
|
|
|
n |
|
|
n |
|
|
|
|
n |
|
2n−1 |
|
|||||||||||
вложенных отрезках имеется точка |
c, |
|
принадлежащая всем построенным отрезкам. До- |
|||||||||||||||||||||||||||
кажем, что |
lim xn = c. Пусть задано ε > 0. Для этого ε подберем номер N |
так, чтобы |
||||||||||||||||||||||||||||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
||||
при всех |
m > N и |
|
n > N выполнялось неравенство |
|xm − xn| |
< |
|
. Далее, выберем |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||||||
число k |
так, чтобы было |
b1 − a1 |
< |
ε |
; это возможно, т.к. |
lim |
b1 − a1 |
= 0 (см. выше |
||||||||||||||||||||||
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2k−1 |
|
|
|
|
|
|
|
|
k→∞ |
2k−1 |
|
|||||||||
пример на вычисление предела |
lim qk |
при 0 < q < 1). |
|
Поскольку отрезок |
[ak, bk] со- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
держит (по построению) бесконечно много элементов последовательности {xn}, то среди
этих элементов найдется такой элемент |
xn0 , для которого |
|
|
n0 > N. Поэтому при n > N |
|||||||||||||||||||||||
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеем |xn0 − xn| < |
|
|
. Кроме того, т.к. |
c [ak, bk], то |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
c |
x |
n0 | |
6 |
b |
k − |
a |
|
= |
b1 − a1 |
< |
ε |
, т.е. |
| |
c |
− |
x |
n0 | |
< |
|
ε |
|
||||
|
|
|
2k−1 |
|
2 |
||||||||||||||||||||||
|
| − |
|
|
|
k |
|
2 |
|
|
|
|
|
|||||||||||||||
Поэтому при всех |
n > N имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|c − xn| = |c − xn0 + xn0 − xn| 6 |c − xn0 | + |xn0 − xn| < |
|
ε |
+ |
|
ε |
= ε, т.е. |c − xn| < ε, |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||
и последовательность |
{xn} |
имеет своим пределом число |
|
|
c. |
Достаточность доказана. |
|||||||||||||||||||||
Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя общее определение монотонной функции к последовательности (а последовательность есть по определению (числовая) функция натурального аргумента), приходим к понятию монотонной последовательности. В качестве примера рассмотрим определение неубывающей последовательности: последовательность {xn} называется неубывающей,
если xn 6 xn+1, n = 1, 2, . . . .
Теорема (о пределе монотонной последовательности). Монотонная последователь-
ность сходится тогда и только тогда, когда она ограничена.
Доказательство. Необходимость. Требуется доказать, что если монотонная последовательность сходится, то она ограничена. Мы знаем однако, что это утверждение справедливо и без предположения о монотонности последовательности (см. выше теорему об ограниченности сходящейся последовательности). Необходимость доказана.
Достаточность. Требуется доказать, что если монотонная последовательность ограничена, то она имеет предел. Рассмотрим это утверждение для неубывающей последовательности {xn}. Ограниченность снизу здесь не имеет значения: всякая неубывающая последовательность ограничена снизу, например, числом x1. Важна ограниченность сверху. Поскольку непустое множество элементов последовательности ограничено сверху, то это множество имеет точную верхнюю грань M. Пусть задано ε > 0. Для точной верхней грани M выполнены, как известно, два условия:
1)xn 6 M для n = 1, 2, . . . ;
2)существует элемент xN последовательности {xn}, для которого xN > M − ε.
Для элементов последовательности xn, у которых n > N неравенство xn > M − ε будет выполнено и подавно, т.к. данная последовательность не убывает, и xn > xN . Таким образом, при всех n > N имеем такое двойное неравенство:
M − ε < xn 6 M.
5

Следовательно, M −ε < xn < M +ε, что равносильно неравенству |M −xn| < ε. Т.к. последнее неравенство выполняется при всех n > N, то последовательность {xn} сходится (к числу M ). Для неубывающей последовательности достаточность доказана; для невозрастающей последовательности доказательство аналогично. Достаточность доказана. Теорема доказана.
Поскольку в этой теореме представляет интерес лишь утверждение о достаточности, причем для неубывающей (возрастающей) последовательности важна ограниченность сверху, а для невозрастающей (убывающей) последовательности — ограниченность снизу, то обычно используют два следствия из рассмотренной теоремы: если последовательность не убывает (возрастает) и ограничена сверху, то она имеет предел, а если последовательность не возрастает (убывает) и ограничена снизу, то она также имеет предел.
|
Пример. Рассмотрим последовательность xn = 1 + |
1 |
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
. Докажем, что эта последо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
вательность имеет предел. |
|
Для этого рассмотрим вспомогательную последовательность |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yn = 1 + |
|
|
|
|
|
|
и докажем, что она убывает. В самом деле, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
yn |
|
|
1 |
|
n+1 |
|
|
|
1 |
|
|
|
|
n+2 |
|
|
n + 1 |
|
|
n + 1 |
n+1 |
|
n + 1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
= 1 + |
|
|
|
: 1 + |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
· |
|
|
= |
||||||||||||||||
|
|
|
|
yn+1 |
n |
n + 1 |
|
|
|
|
|
|
|
|
n |
n + 2 |
|
|
|
n + 2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + |
|
|
1 |
|
|
|
|
|
n+1 |
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 + 2n |
|
n + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Применим неравенство Бернулли: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
yn |
|
|
|
1 |
|
|
|
n+1 |
|
n + 1 |
|
|
|
|
|
|
|
n + 1 |
|
|
|
n + 1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= 1 + |
|
|
|
|
· |
|
|
|
|
|
> |
1 + |
|
|
|
· |
|
|
> |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
yn+1 |
n2 + 2n |
|
n + 2 |
n2 + 2n |
n + 2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
· |
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
> 1 + |
|
|
|
|
= 1, т.е. yn > yn+1. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n + 1 |
n + 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
Таким образом |
, |
последовательность |
|
|
{yn} |
|
убывает |
. |
|
|
Очевидно |
|
она ограничена снизу |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||
( |
например |
, |
нулём |
Поэтому существует |
|
|
lim |
|
|
1 + |
1 |
|
|
|
|
|
= e. |
Таким же будет и предел |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
исходной последовательности {xn} : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
1 + 1 |
n+1 |
|
|
|
|
lim 1 + n1 |
n+1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
nlim xn |
= nlim |
|
1 + |
|
|
|
= nlim |
|
|
|
|
|
|
|
|
|
= |
|
|
|
lim |
1 + |
1 |
|
|
= e. |
||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
1 + |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
→∞ |
|
→∞ |
|
|
|
|
|
→∞ |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|||||
Приближенное значение e таково: e ≈ 2, 718281828459045, причем верны все написанные знаки. Запомнить их нетрудно: после 2,7 пишем два раза год рождения писателя Л.Н.Толстого, а затем углы равнобедренного прямоугольного треугольника.
6
кафедра «Математическое моделирование» проф. П. Л. Иванков
Математический анализ
конспект лекций
для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)
Лекция 5.
Гиперболические функции, их свойства и графики. Два определения предела функции в точке (предел по Коши и предел по Гейне). Теорема об эквивалентности этих определений. Геометрическая иллюстрация предела. Предел функции в бесконечности. Бесконечные пределы. Единственность предела функции. Локальная ограниченность функции, имеющей конечный предел. Теорема о сохранении функцией знака своего предела. Предельный переход в неравенстве. Теорема о пределе промежуточной функции.
ОЛ-1, пп. 7.1, 7.3, 7.4, 7.8
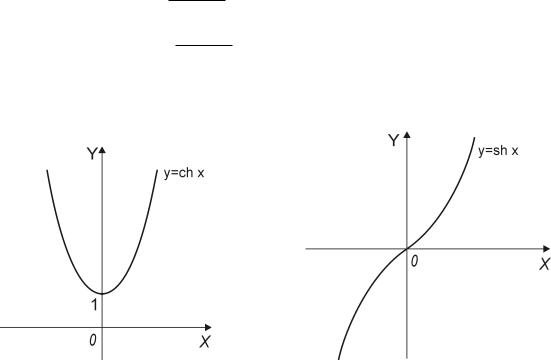
При решении многих задач оказываются полезными гиперболические функции:
сh x = ex + e−x — гиперболический косинус; 2
sh x = ex − e−x — гиперболический синус; 2
th x = |
sh x |
, |
cth x = |
сh x |
— гиперболические тангенс |
|
сh x |
sh x |
|||||
|
|
|
и котангенс соответственно. |
|||
|
|
|
|
|
1

Свойства гиперболических функций похожи на соответствующие свойства тригономе-
трических функций. Например, |
|
|
|
|
|
|
|
|
sh(x ± y) = sh x · сh y ± sh y · сh x, |
сh(x ± y) = сh x · сh y ± sh x · sh y. |
|
||||||
Из последнего равенства при x = y |
в случае знака минус получаем |
|
|
|
|
|||
|
|
|
сh2 x − sh2 x = 1. |
|
|
|
|
|
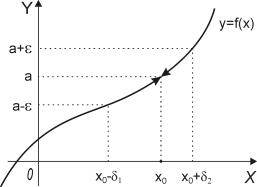
Пусть функция |
f(x) определена в проколотой окрестности точки |
x0. |
Число |
a |
||||
называется пределом функции |
f(x) при x → x0, если для любого |
ε > 0 |
существует |
|||||
положительное число δ = δ(ε) |
такое, что если 0 < |x − x0| < δ, то |f(x) − a| < ε. |
|
||||||
Это — определение предела по Коши. Определение предела по Гейне выглядит так. |
||||||||
Пусть функция |
|
|
|
˚ |
точки x0. Число |
|||
f(x) определена в проколотой окрестности U (x0) |
||||||||
a называется пределом функции f(x) при |
x → x0, если для любой последовательности |
|||||||
˚ |
|
|
nlim xn = x0, выполняется равенство |
nlim f(xn) = a. |
||||
{xn} точек из U (x0), для которой |
||||||||
|
|
|
→∞ |
|
|
→∞ |
|
|
Эти определения эквивалентны, |
т.е. с их помощью вводится одно и то же понятие. |
|||||||
Чтобы убедиться в этом, требуется доказать два утверждения. |
|
|
|
|
||||
Пусть сначала |
a является пределом функции f(x) при x → x0 |
в смысле определе- |
||||||
ния по Коши. Проверим, что при этом будут также выполнены требования определения по Гейне. Пусть задана последовательность точек {xn}, все элементы которой лежат в
|
|
˚ |
|
и пусть |
lim xn = x0. Если задано |
ε > 0, то в соот- |
|
проколотой окрестности U (x0), |
|||||||
|
|
|
|
|
n→∞ |
|
|
ветствии с определением предела по Коши найдется δ = δ(ε) > 0 |
такое, что для всех |
||||||
˚ |
|
|
| < δ, выполняется неравенство |
|f(x) − a| < ε. Поскольку |
|||
x U (x0), для которых |x − x0 |
|||||||
lim xn = x0, то найдется номер |
N такой, что при всех n > N |
выполняется неравенство |
|||||
n→∞ |
|
|f(xn) − a| < ε. Таким образом, при n > N выполняется неравен- |
|||||
|xn − x0| < δ, а тогда |
|||||||
ство |
|f(xn) − a| < ε, |
т.е. |
nlim f(xn) = a, |
и число a является пределом функции f(x) |
|||
|
|
|
→∞ |
|
|
|
|
при |
x → x0 в смысле определения по Гейне. |
|
|
||||
Предположим теперь, что a |
является пределом функции f(x) при x → x0 в смысле |
||||||
определения по Гейне. Доказательство того, что a будет также пределом в смысле определения по Коши удобнее провести методом от противного. Если требования определения
по Коши не выполняются, то найдется |
ε0 |
> 0 |
такое, что при любом положительном |
||||||||||
δ существует число |
˚ |
|
|
|
|
|x − x0| < δ, однако |
|f(x) − a| > ε0. |
||||||
x U (x0), для которого |
|||||||||||||
Зафиксировав такое |
ε0, при каждом |
n = 1, 2, . . . подберем такое |
xn |
˚ |
что |
||||||||
U (x0), |
|||||||||||||
1 |
|
и при этом |f(xn) − a| > |
|
|
|
Из последнего неравенства следует, |
что |
||||||
|xn − x0| < |
|
, |
ε0. |
|
|||||||||
n |
|
||||||||||||
a не является пределом последовательности |
{f(xn)} при n → ∞. |
Чтобы доказать, |
|||||||||||
что lim xn |
= x0 заметим, что для любого положительного числа |
ε |
при некотором |
||||||||||
n→∞ |
|
|
|
|
|
1 |
< ε. Ясно, что тогда при любом n > N |
||||||
натуральном |
|
N |
выполняется неравенство |
||||||||||
|
|
N |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
1 |
|
|
|
|
|
|
|
|
|
|
выполняется также неравенство |xn − x0| < |
|
|
|
< ε, т.е. |
|xn − x0| < ε. Это означает |
||||||||||||||||||||
n |
N |
||||||||||||||||||||||||
, что |
nlim xn = x0. |
Таким образом, xn → x0 |
при |
n → ∞, |
|
и в то же время {f(xn)} |
|||||||||||||||||||
|
→∞ |
|
|
|
n → ∞. |
Полученное противоречие означает, |
|
|
|||||||||||||||||
не стремится к |
a |
при |
что доказываемое |
||||||||||||||||||||||
утверждение справедливо. Эквивалентность двух определений предела доказана. |
|
||||||||||||||||||||||||
Если a |
есть предел функции |
f |
( |
x |
) |
|
при |
x |
→ |
0 |
, |
то пишут a |
= x x0 |
или |
|||||||||||
|
|
|
|
|
x |
lim f(x), |
|||||||||||||||||||
f(x) → a |
|
x → x0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|||
при |
По ходу доказательства эквивалентности двух определений |
||||||||||||||||||||||||
предела мы воспользовались тем, |
что для любого (сколь угодно малого) числа ε0 |
> 0 |
|||||||||||||||||||||||
найдется натуральное |
N |
такое, |
что |
|
1 |
< ε0, т.е. |
|
N > |
|
1 |
. Справедливость этого |
||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
ε0 |
|
|
||
утверждения следует из аксиомы Архимеда: для любого вещественного числа существует превосходящее его натуральное число. Опираясь на существование точной верхней грани у всякого непустого ограниченного сверху множества действительных чисел, можно доказать аксиому Архимеда. В самом деле, пусть существует действительное число E такое, что n 6 E для любого n N (здесь E – заглавная греческая буква эпсилон; эту букву часто используют для обозначения «сколь угодно большого числа», в отличие от буквы ε, служащей для обозначения «сколь угодно малого числа» (например, в определении
предела)). Тогда N — непустое ограниченное сверху подмножество |
R. |
Следовательно, |
||
у этого множества существует точная верхняя грань n0. Для числа |
n0 |
выполнены два |
||
условия: |
n N выполняется неравенство n 6 n0; |
|
|
|
1) |
для любого |
|
|
|
2) |
для любого |
ε > 0 существует n N такое, что n > n0 − ε. |
|
|
Взяв ε = 1, получим, что n > n0 − 1, т.е. n + 1 > n0, а т.к. n + 1 — натуральное число, то мы получаем противоречие с первым условием. Таким образом, точная верхняя грань n0 не существует, и множество N не является ограниченным сверху, т.е. аксиома Архимеда справедлива.
На рисунке показана геометрическая иллюстрация предела: чтобы по заданному ε > 0
подобрать δ = δ(ε) > 0, |
о котором говорится в определении предела (по Коши), доста- |
||||||
точно взять минимальное из чисел δ1 и δ2. |
|
|
|
|
|||
Рассмотрим теперь функцию f(x), |
определенную в некоторой окрестности точки +∞, |
||||||
т.е. на интервале (x0, +∞). Число a |
называется пределом функции f(x) при x → +∞, |
||||||
если для любого ε > 0 существует число E (не меньшее x0) такое, что при всех |
x > E |
||||||
выполняется неравенство |
|f(x) − a| < ε. Это — определение по Коши. |
Можно сфор- |
|||||
мулировать и определение по Гейне: |
число |
a называется пределом функции |
f(x) |
||||
при x → ∞, если для всякой последовательности точек {xn} интервала |
(x0, +∞) из |
||||||
условия |
nlim xn = +∞ вытекает равенство |
nlim f(xn) = a. |
Эти определения экви- |
||||
|
→∞ |
|
|
→∞ |
x → x0. |
|
|
валентны; доказательство проводится так же, |
как и в случае |
Обозначение: |
|||||
a = lim |
f(x), или f(x) → a при x → +∞. |
|
|
|
|
||
Следует отметить, что в теории последовательностей мы не рассматривали ситуацию
3

из последнего определения, когда lim xn = +∞. Говорят, что последовательность {xn}
n→∞
имеет пределом |
+∞, если для любого числа E |
существует номер N такой, что |
при всех n > N |
выполняется неравенство xn > E. |
Аналогично определяются пределы |
lim xn = −∞, и lim xn = ∞. Надо только в последнем определении неравенство xn > E
n→∞ n→∞
заменить соответственно на xn < E и |xn| > E.
Эти определения без труда переносятся на случай функций. Запись lim f(x) = +∞
x→x0
для функции, определенной в проколотой окрестности точки x0, означает, что для любого E найдется положительное число δ такое, что если 0 < |x − x0| < δ, то f(x) > E. Если последнее неравенство заменить соответственно на f(x) < E или |f(x)| > E, то получим определения того, что f(x) → −∞ или f(x) → ∞ при x → x0.
Рассмотрим теорему о единственности предела функции.
Теорема (о единственности предела функции). Функция f(x), определенная в про-
колотой окрестности точки x0, может иметь не более одного предела при x → x0.
Доказательство. Пусть |
a |
lim f(x) и b = |
lim f(x), |
причем |
a |
6= |
b. |
Для положи |
- |
|||||||||||||
|
|
|
|
|
= x x0 |
|
|
x |
→ |
x0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
→ |
|
|
|
|
|
|
| |
|
− |
|
0| |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
тельного числа ε = |
|a − b| |
найдется |
δ |
|
> 0 такое, что при |
0 < |
|
x |
|
x |
|
< δ |
|
выполняется |
||||||||
|
|
|
|
|
|
|||||||||||||||||
неравенство |
|f(x) − a| < ε, и число |
δ2 > 0 такое, что при |
0 < |x − x0| < δ2 |
выполняется |
||||||||||||||||||
неравенство |
|f(x) − b| < ε. |
Если |
δ = min(δ1, |
δ2), то при 0 < |x − x0| < δ имеем |
||||||||||||||||||
|a −b| = |(a −f(x)) + (f(x) −b)| 6 |a −f(x)|+ |f(x) −b| < 2ε = |a −b|, т.е. |a −b| < |a −b|
— противоречие. Теорема доказана.
Теорема (о локальной ограниченности функции, имеющей предел). Для функции f(x), имеющей (конечный) предел при x → x0 существует проколотая окрестность этой точки, на которой данная функция ограничена.
Доказательство. Пусть a = lim f(x). Тогда для положительного числа 1 найдется
x→x0
δ > 0 такое, что при 0 < |x − x0| < δ выполняется неравенство |f(x) − a| < 1. Отсюда
|f(x)| = |f(x) − a + a| 6 |f(x) − a| + |a| < 1 + |a|, т.е. |f(x)| < 1 + |a|,
и мы видим, что f(x) ограничена в проколотой δ-окрестности (x0 − δ, x0) (x0, x0 + δ) точки x0. Теорема доказана.
Теорема (о сохранении функцией знака своего предела). Пусть предел |
lim f(x) |
||||||||||||
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
положителен. Тогда функция |
f(x) положительна в некоторой проколотой окрестности |
||||||||||||
точки x0. |
|
|
|
|
|
|
|
|
a |
||||
Доказательство. Пусть |
lim f(x) = a, a > 0. Тогда для положительного числа |
|
|||||||||||
|
2 |
|
|||||||||||
x→x0 |
|
|
|
|
|
|
|
||||||
найдется δ > 0 такое, что при 0 < |x −x0| < δ выполняется неравенство |f(x) −a| < |
|
a |
|||||||||||
|
|
|
. |
||||||||||
2 |
|||||||||||||
|
|
|
a |
a |
|
a |
|||||||
Это неравенство равносильно такому: |
− |
|
< f(x) − a < |
|
; следовательно, |
f(x) > |
|
, |
|||||
2 |
2 |
2 |
|||||||||||
т.е. данная функция положительна при |
x (x0 − δ, x0) (x0, x0 + δ). Теорема доказана. |
||||||||||||
Переформулированные соответствующим образом последние три теоремы остаются в
силе и для других рассмотренных выше предельных процессов. |
|
|
Теорема (о предельном переходе в неравенстве). Пусть функции |
f(x) |
и g(x) опре- |
˚ |
|
˚ |
делены в проколотой окрестности U (x0) точки x0, причем для любого |
x U (x0) выпол- |
|
няется неравенство f(x) > g(x). Тогда, если эти функции имеют пределы |
a = lim f(x) |
|
|
|
x→x0 |
и b = lim g(x), то a > b.
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
Пусть вопреки |
утверждению теоремы |
|
0| |
a |
< b, |
и пусть |
||||||
2 |
|
1 |
|
| |
|
− |
|
|
1 |
|
|
||
ε = |
b − a |
> 0. Тогда существует δ > 0 |
такое, что при 0 < |
|
x |
|
x |
|
< δ |
|
имеет место не- |
||
|
|
|
|
|
|||||||||
4
равенство |f(x) −a| < ε, т.е. a−ε < f(x) < a+ ε. Аналогично существует δ2 > 0 такое,
что при 0 < |x−x0| < δ2 |
|
выполняется неравенство |g(x)−b| < ε, т.е. b−ε < g(x) < b+ε. |
|||||||||||||||
Если |
|
|
|
и |
0 < |x − x0| < δ, |
то |
|
|
|
|
a + b |
− ε < g(x), т.е. |
|||||
δ = min(δ1, δ2), |
|
f(x) < a + ε = |
|
|
= b |
||||||||||||
|
2 |
|
|||||||||||||||
f(x) < g(x) для указанных значений x — противоречие. Теорема доказана. |
|
||||||||||||||||
|
Замечание. |
Если в условии теоремы неравенство |
|
f(x) > g(x) |
заменить на строгое, |
||||||||||||
т.е. если f(x) > g(x), |
|
то отсюда, вообще говоря, не следует, что |
a > b. Например, при |
||||||||||||||
x |
< 1, x = 0, |
имеем |
| |
x |
| |
> x2. В то же время |
lim |
x |
| |
= lim x2 = 0. |
|
|
|
|
|||
| | |
|
6 |
|
|
|
|
x→0 | |
|
x→0 |
|
|
|
|
|
|||
|
Теорема (о пределе |
промежуточной |
функции). |
Пусть |
для всех |
x |
из неко- |
||||||||||
торой |
|
|
|
|
|
˚ |
|
x0 |
|
|
выполняется |
двойное неравенство |
|||||
проколотой окрестности U (x0) точки |
|
|
|||||||||||||||
f(x) 6 g(x) 6 h(x) , и пусть существуют пределы |
|
|
lim f(x) |
и |
lim h(x), |
равные од- |
|||||||||||
ному и тому же числу |
|
a. Тогда и lim g(x) = a. |
|
x→x0 |
|
x→x0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Для произвольного положительного числа ε |
существуют положи- |
|||||||||||||||
тельные числа |
δ1 и δ2 |
|
такие, что при |
0 < |x − x0| < δ1 |
имеет место неравенство |
||||||||||||
|f(x) −a| < ε, т.е. a −ε < f(x) < a + ε, а при |
0 < |x −x0| < δ2 |
выполняется неравенство |
|||||||||||||||
|h(x) − a| < ε, |
т.е. a − ε < h(x) < a + ε. Тогда при |
0 < |x − x0| < δ, |
δ = min(δ1, δ2), |
||||||||||||||
выполняется неравенство |
a − ε < f(x) 6 g(x) 6 h(x) < a + ε, т.е. a − ε < g(x) < a + ε, и |
||||||||||||||||
|g(x)−a| < ε. Таким образом, при 0 < |x−x0| < δ имеет место неравенство |g(x)−a| < ε. Это означает, что lim g(x) = a. Теорема доказана.
Заметим, что аналоги доказанных теорем справедливы и для других рассмотренных выше предельных процессов (в том числе и в теории последовательностей).
5
кафедра «Математическое моделирование» проф. П. Л. Иванков
Математический анализ
конспект лекций
для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)
Лекция 6.
Односторонние пределы. Теорема о замене переменной в пределе (о пределе сложной функции). Арифметические операции с функциями, имеющими пределы. Первый и второй замечательные пределы. Следствия из них.
ОЛ-1, пп. 7.2, 7.4-7.7
Пусть функция f(x) |
определена при x0 < x < x0 +η, где η − некоторое положитель- |
|
ное число. Говорят, что |
a есть предел функции f(x) |
при x → x0+, если для любого |
ε > 0 существует δ = δ(ε) > 0 такое, что при любом |
x, x0 < x < x0 + δ, выполняется |
|
неравенство |f(x) − a| < ε. Такой предел называют правосторонним или пределом при
x |
→ |
x |
0 |
справа |
. |
Обозначение |
: |
lim f(x) = a. Аналогично можно определить предел |
||||||||
|
|
|
|
x x0+ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
lim |
f(x) при условии, что функция |
f(x) |
задана при x |
|
− |
η < x < x |
; η > 0. |
|||||||||
x→x0− |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
||
|
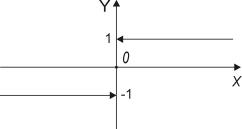
Пример. Рассмотрим функцию («сигнум икс») |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1, |
если |
x > 0, |
|
|
|
|
|
|
|
|
|
|
sign x = |
0, |
если |
x = 0, |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1, |
если |
x < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
Очевидно, lim sign x = −1, lim sign x = 1.
Теорема (о пределе сложной функции). Пусть функция f(x) определена в проколотой
окрестности точки 0 и принимает значения в проколотой окрестности ˚ 0 точки 0 x V (y ) y ,
˚
причём lim f(x) = y0. Тогда, если функция g(y) определена на V (y0), и lim g(y) = a, то и lim g(f(x)) = a.
Доказательство. Пусть задано ε > 0. Т.к. lim g(y) = a, то для ε найдётся δ = δ(ε) > 0
такое, что при 0 < |y − y0| < δ выполняется неравенство |g(y) − a| < ε. Для положительного числа δ в силу равенства lim f(x) = y0 существует число η = η(δ) > 0 такое, что при
1
всех x, 0 < |x −x0| < η, имеет место неравенство |f(x) −y0| < δ; при этом в силу того, что
˚ |
, выполняется также неравенство |f(x) − y0| > 0. |
f(x) V (y), и, следовательно, f(x) 6= y0 |
Таким образом, по заданному ε > 0 мы нашли η > 0 такое, что при всех x, 0 < |x−x0| < η, выполняется неравенство 0 < |f(x) − y0| < δ; в таком случае для всех указанных x выполняется неравенство |g(f(x)) − a| < ε. Это означает, что lim g(f(x)) = a. Теорема
x→x0
доказана.
Замечание. Теорема остаётся в силе, если какие-либо из чисел x0, y0 или a заменить символами −∞, +∞ или ∞. Можно также рассмотреть аналоги доказанной теоремы, в которых фигурируют односторонние пределы. Ограничение f(x) 6= y0 можно отбросить, если функция g(y) определена при y = y0, и g(y0) = a.
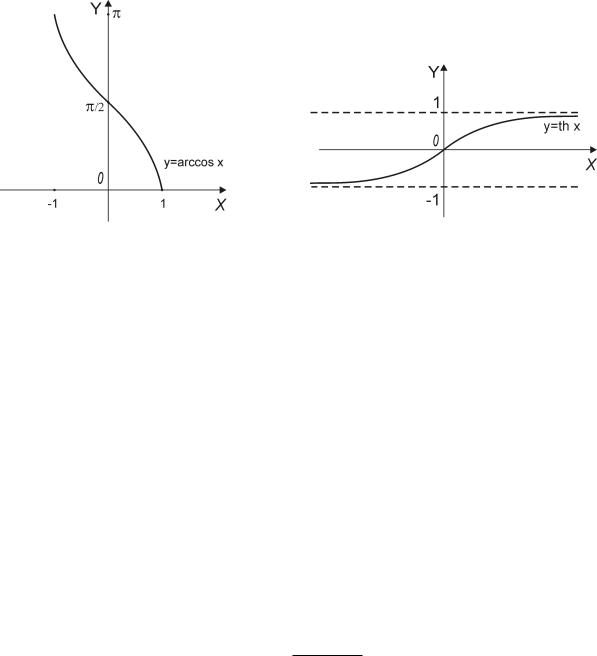
Пример. Найти пределы lim arccos th x и |
lim arccos th x. |
x→−∞ |
x→+∞ |
Из графика арккосинуса ясно, что lim arccos y = π и lim arccos y = 0. Для доказатель-
ства этих равенств следует воспользоваться непрерывностью арккосинуса, которая будет рассмотрена ниже. Поскольку th x → −1 при x → −∞, и th x → 1 при x → +∞, причём всегда | th x| < 1, то arccos th x → π при x → −∞, и arccos th x → 0 при x → +∞.
|
|
Теорема |
(об |
|
арифметических |
операциях |
|
|
|
над |
функциями, |
имею- |
|||||||||||
щими предел). |
|
Пусть |
lim f(x) |
= |
a, |
|
|
lim g(x) |
= |
b. |
Тогда |
||||||||||||
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
x→x0 |
|
|
|
|
|
|||
lim (f(x) |
± |
g(x)) = a |
± |
b, |
lim f(x) |
· |
g(x) |
= ab, |
lim |
|
f(x) |
= |
|
a |
. |
Последнее равен- |
|||||||
|
|
||||||||||||||||||||||
x |
→ |
x0 |
|
|
|
|
x x0 |
|
|
x |
→ |
x0 |
|
g(x) |
|
b |
|
|
|||||
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ство справедливо при |
|
b |
6= 0, а также при условии, что g(x) 6= 0 |
для всех |
x из |
||||||||||||||||||
некоторой проколотой окрестности точки x0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Доказательство. |
|
Утверждение теоремы можно вывести из доказанных выше тео- |
|||||||||||||||||||
рем об арифметических операциях над сходящимися последовательностями, используя
определение предела функции по Гейне. |
Рассмотрим, например, |
утверждение о пре- |
||||||||||||||||
деле частного. |
Пусть |
˚ |
|
— проколотая |
окрестность точки |
x0, |
в которой |
опре- |
||||||||||
U (x0) |
||||||||||||||||||
делены функции |
f(x) |
и |
g(x), |
причем |
g(x) |
6= 0 |
|
|
|
|
˚ |
|
|
|
|
|
||
для любого x U (x0). Рассмо- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˚ |
|
|
и |
|
трим произвольную последовательность {xn}, все элементы которой лежат в U (x0), |
|
|||||||||||||||||
при этом lim xn = x0. |
По определению предела функции по Гейне имеем равенства |
|||||||||||||||||
x→x0 |
nlim g(xn) = b, |
причем g(xn) 6= 0, |
|
|
|
|
|
|
|
|
|
|
||||||
nlim f(xn) = a и |
n = 1, 2, .... По теореме о пределе |
|||||||||||||||||
→∞ |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частного из теории последовательностей |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f(xn) |
|
lim f(xn) |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
= |
n→∞ |
|
= |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n→∞ g(xn) |
lim g(xn) |
|
b |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
Поэтому в соответствии с определением предела функции по Гейне |
lim |
f(x) |
= |
a |
. |
|||||||||||||
g(x) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
b |
|||
Аналогично можно доказать два оставшихся утверждения теоремы. Теорема доказана.
2
