
MAall
.pdf
Теорема |
(о |
первом замечательном |
|
пределе). |
Имеет место равенство |
||||
|
|
lim |
sin x |
= 1 . |
|
||||
|
|
|
|
|
|||||
|
|
x→0 |
|
x |
|
|
|
||
Доказательство. Т.к. функция lim |
sin x |
|
является чётной, то достаточно доказать ра- |
||||||
|
x |
||||||||
|
sin x |
x→0 |
|
|
|
|
|||
венство lim |
= 1. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
x→0+ |
|
|
|
|
|
|
|
|
|
π
Пусть 0 < x < 2 . Рассмотрим окружность радиуса R с центром в начале координат,
пересекающую ось абсцисс в точке A, и пусть угол AOB равен x (радиан). Пусть, далее, CA — перпендикуляр к этой оси, C — точка пересечения с этим перпендикуляром продолжения отрезка OB за точку B. Тогда площадь 4OAB меньше площади сектора OAB, а площадь этого сектора меньше площади 4OAC, т.е.
1 |
R2 sin x < |
1 |
R2x < |
1 |
R2 tg x , и |
|
||||||
|
|
|
|
|
|
|
|
|||||
2 |
2 |
2 |
|
|||||||||
|
|
sin x |
|
|
|
|||||||
|
cos x < |
|
< 1 . |
(1) |
||||||||
|
x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы можно было применить теорему о пределе промежуточной функции, достаточно
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
||
доказать, что cos x → 1 при x → 0+. Т.к. 0 < sin x < x при 0 < x < |
|
|
(это следует из |
||||||||||||||
|
2 |
||||||||||||||||
доказанного; |
на |
деле неравенство верно при всех |
|
то |
при |
|
|
|
Отсюда |
||||||||
2 x |
|
|
|
x > 0), |
|
sin x → 02 x |
|
|
x → |
0+. |
|
||||||
следует, что sin |
|
|
→ 0 при x → 0+, а поскольку cos x = 1 − 2 sin |
|
|
, то cos x → 1 при |
|||||||||||
2 |
2 |
||||||||||||||||
x → 0+. Поэтому из (1) вытекает требуемое. Теорема доказана. |
|
|
|
|
|
|
|||||||||||
Теорема |
(о |
втором замечательном |
пределе). |
Справедливо |
равенство |
||||||||||||
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
= e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x→∞ 1 + x |
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Требуется доказать, что |
|
|
|
|
|
|
|
|
|
|
|
||||||
lim |
1 |
x |
e |
и lim |
1 |
|
x |
e . |
|
|||
|
|
|
|
|
|
|
|
|||||
1 + x |
= |
1 + x |
= |
(2) |
||||||||
x→+∞ |
|
x→−∞ |
|
|||||||||
Рассмотрим первое из этих равенств. Имеем [x] 6 x < [x] + 1, где [x] — целая часть x. При x > 1 (при этом [x] > 0) получаем отсюда:
1 + |
1 |
> 1 + |
|
1 |
> 1 + |
|
1 |
|
, |
|
[x] |
x |
[x] + 1 |
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
[x]+1 |
1 |
|
x |
|
1 |
|
|
[x] |
|
|||||
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
|
> 1 + |
|
|
|
|
> 1 + |
|
|
|
. |
(3) |
||
|
|
|
|
|
|
|
[x] |
|
|
|
x |
|
[x] + 1 |
|||||||||||||
. |
. |
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n→∞ 1 + n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Т к |
|
lim |
|
|
|
= e , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
n+1 |
|
|
|
|
1 |
n |
1 |
|
|
|
|
|
|
|
|
|
|||||||
n→∞ 1 + n |
|
|
n→∞ |
1 + n |
|
· 1 + n = |
|
|
|
|
|
|
||||||||||||||
lim |
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3

|
|
|
|
|
|
|
|
= n→∞ |
1 |
|
|
n |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
n |
· n→∞ |
1 + n |
||||||||
n→∞ |
1 + n + 1 |
n |
|
|
|
|
, |
lim |
1 + |
|
|
|
lim |
|
|
= e . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично и lim |
1 |
|
|
e. Таким образом для вспомогательных функций |
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
n+1 |
|
|
|
1 |
|
|
|
n |
|
|
|
|
|
g1(n) = 1 + |
|
|
|
и g2(n) = 1 + |
|
|
|
|
|
|
|
|||||||
|
n |
|
n + 1 |
|
|
|
|
||||||||||||
натурального аргумента n имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
lim g1(n) = lim g2(n) = e. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n→∞ |
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
Если x → +∞, то и целая часть [x] → +∞. Следовательно, по теореме о пределе сложной функции g1([x]) → e и g2([x]) → e при x → +∞. Отсюда и из (3) по теореме о пределе про-
межуточной функции получаем первое из соотношений (2). |
Для доказательства второго |
||||||||||||||||||
из этих соотношений вновь применим теорему о пределе сложной функции: |
|||||||||||||||||||
x→−∞ |
|
1 |
|
x |
|
1 |
|
−y |
|
1 |
|
|
y−1 |
|
1 |
|
|||
|
x |
|
y→+∞ 1 + −y |
y→+∞ |
y − 1 |
|
y − 1 |
||||||||||||
lim |
1 + |
|
|
= |
lim |
|
|
= lim |
1 + |
|
|
|
|
1 + |
|
= e. |
|||
Итак, справедливость обоих равенств (2) установлена, и теорема доказана. |
|||||||||||||||||||
Замечание. |
Нетрудно убедиться, что утверждение теоремы о втором замечательном |
||||||||||||||||||
пределе равносильно равенству lim(1 + t)1/t. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
t→0 |
|
|
|
|
|
|
|
|
|
|||
Если в выражении |
lim |
f(x) |
числитель и знаменатель стремятся к нулю, т.е. если |
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
x→x0 |
g(x) |
|
|
|
|
|
|
|
|
|
||||
lim f(x) = |
lim g(x) = 0, то нельзя непосредственно применить теорему о пределе част- |
||||||||||||||||||
x→x0 |
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0
ного. В этом случае говорят, что мы имеем дело с неопределённостью вида 0. Вычисление предела в этой ситуации называется раскрытием неопределённости. При этом в некоторых случаях может оказаться полезной теорема о первом замечательном пределе. Например
lim |
sin 2x |
= lim |
2 |
· |
sin 2x |
· |
|
3x |
· |
cos 3x = |
|
2 |
. |
|
3 |
2x |
sin 3x |
|
|||||||||
x→0 tg 3x |
x→0 |
|
3 |
||||||||||
При вычислении предела степенно-показательного выражения u(x)v(x) могут встретиться неопределённости вида 1∞, 00 и ∞0. Первую из них обычно удаётся раскрыть с помощью теоремы о втором замечательном пределе. При этом используется следующее утверждение. Пусть x → x0; тогда, если u(x) → a, a > 0, v(x) → b, то u(x)v(x) → ab. Доказательством этого утверждения мы сейчас заниматься не будем.
|
. |
x→0 |
→ |
|
x |
→ ∞ |
|
Пример |
|
Требуется найти предел lim(1 + sin x)1/x. Здесь 1 + sin x |
|
1, |
1 |
|
, и |
|
|
|
|
мы имеем дело с неопределённостью вида 1∞. Раскрыть эту неопределённость можно, например, так:
x→0 |
x→0 |
sin x |
|
|
|
|
|||
|
1 |
x |
|
|
lim(1 + sin x)1/x = lim (1 + sin x) |
sin x |
|
= e , |
|
т.к. выражение в больших скобках стремится к e по теореме о втором замечательном
пределе, а показатель степени |
sin x |
→ 1 по теореме о первом замечательном пределе. |
x |
||
|
|
4 |
кафедра «Математическое моделирование» проф. П. Л. Иванков
Математический анализ
конспект лекций
для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)
Лекция 7.
Бесконечно малые функции. Связь функции, ее предела и бесконечно малой. Свойства бесконечно малых функций. Бесконечно большие функции, их связь с бесконечно малыми.
ОЛ-1 п. 7.6
Функция ϕ(x) называется бесконечно малой при x → x0, если lim ϕ(x) = 0.
x→x0
Теорема (о связи функции, ее предела и бесконечно малой). Равенство a = lim f(x)
x→x0
имеет место тогда и только тогда, когда f(x) = a + ϕ(x), где функция ϕ(x) бесконечно мала при x → x0.
Доказательство. Необходимость. Пусть a = lim f(x). Требуется доказать, что
x→x0
f(x) = a + ϕ(x), где ϕ(x) − бесконечно малая функция при x → x0. Обозначим ϕ(x) = f(x) −a. Тогда из определения предела функции получаем, что для любого ε > 0 существует число δ = δ(ε) > 0 такое, что при всех x, 0 < |x − x0| < δ, выполняется не-
равенство |
| |
f x |
a |
| |
= | |
ϕ |
x |
)| |
< ε. |
Это означает |
, |
что |
|
lim ϕ(x) = 0, т.е. ϕ(x) |
бесконечно |
|||||||||
|
( ) − |
|
|
( |
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
||||||||
мала при |
x → x0. Необходимость доказана. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Достаточность. Пусть |
f(x) = a + ϕ(x), где функция |
ϕ(x) |
бесконечно мала при |
|||||||||||||||||||||
x → x0. Тогда для любого ε > 0 |
существует число |
|
δ = δ(ε) > 0 |
такое, что при всех |
||||||||||||||||||||
x, 0 < |x − x0| < δ |
выполняется неравенство |
|
|ϕ(x)| < ε, |
а т.к. |
ϕ(x) = f(x) − a, то |
|||||||||||||||||||
также и неравенство |
| |
f |
( |
x |
) |
− |
a |
| |
< ε. Отсюда следует |
, |
что lim f(x) = a. Достаточность |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|||||||
доказана. Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рассмотрим свойства бесконечно малых функций. |
|
|
|
|
|
|
|
|
||||||||||||||||
Теорема (о сумме бесконечно малых). Пусть функции |
ϕ1(x), ..., ϕn(x) |
бесконечно |
||||||||||||||||||||||
малы при |
x → x0. Тогда их алгебраическая сумма |
|
|
n |
|
также бесконечно мала |
||||||||||||||||||
|
=1 ±ϕi(x) |
|||||||||||||||||||||||
при x → x0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iP |
|
|
|
|
|
|||
Доказательство. Очевидно, достаточно доказать теорему для |
n = 2, |
т.е. доказать, |
||||||||||||||||||||||
что бесконечно малой при |
x → x0 является функция ±ϕ1(x) ± ϕ2(x). |
Пусть задано |
||||||||||||||||||||||
ε > 0; из того, |
что |
|
ϕ1(x) |
и ϕ2(x) бесконечно малы при |
x → x0 |
получаем, что |
||||||||||||||||||
существует число |
δ1 = |
εδ1(ε) > 0 |
такое, что при всех |
|
x, 0 < |x − x0| < δ1 , выполняется |
|||||||||||||||||||
неравенство |ϕ1(x)| |
< |
|
|
; |
существует также число |
δ2 |
= δ2(ε) > 0 |
такое, что при всех |
||||||||||||||||
|
2 |
|||||||||||||||||||||||
1
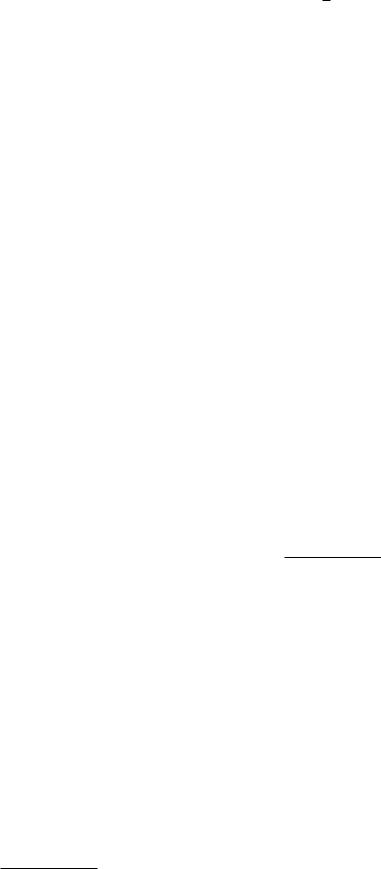
x, 0 < |x − x0| < δ2 , выполняется неравенство |ϕ2(x)| < 2ε. Если δ = min(δ1, δ2), то при всех x, 0 < |x − x0| < δ , имеем
|
|
|
|
|
|
|
|
|
|
|
| ± |
ϕ1(x) ± ϕ2(x)| 6 |ϕ1(x)| + |ϕ2(x)| < |
|
ε |
|
|
ε |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
= ε. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
Отсюда |
|
|
lim ( ϕ |
(x) |
± |
|
ϕ |
(x)) = 0, т.е. функция |
± |
ϕ |
(x) |
± |
ϕ |
(x) |
бесконечно мала при |
|||||||||||||||||||||||||||
|
|
|
|
|
x x0 |
± |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
x → x0, |
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
и теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Теорема (о произведении бесконечно малой величины на ограниченную). |
Пусть в |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˚ |
|
|
|
заданы функции |
|
f(x) и ϕ(x), |
причем |
|
|
f(x) |
|||||||||||||||||
проколотой окрестности U (x0) точки x0 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
˚ |
|
|
|
ϕ(x) |
бесконечно мала при x → x0. Тогда произведение f(x)·ϕ(x) |
|||||||||||||||||||||||||||||
ограничена на U (x0), а |
||||||||||||||||||||||||||||||||||||||||||
есть бесконечно малая функция при x → x0. |
|
|
|
|
|
|
|
|
|
|
˚ |
|
|
|
то существует число |
|||||||||||||||||||||||||||
|
Доказательство. Т.к. f(x) |
ограничена на множестве U (x0), |
||||||||||||||||||||||||||||||||||||||||
c |
такое |
, |
|
что |
|
|
|
|
|
|
|
c |
при всех x |
|
˚ |
x |
0) |
. |
Далее |
, |
|
пусть задано |
ε |
> |
0 |
. |
Для |
|||||||||||||||
|
|
|
|
|
|
|f(x)| 6 ε |
|
|
|
U ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
положительного числа |
|
|
|
|
(т.к. с > 0, то c + 1 6= 0) |
существует |
δ > 0 |
такое, что при |
||||||||||||||||||||||||||||||||||
|
c + 1 |
|||||||||||||||||||||||||||||||||||||||||
всех x, 0 < |x − x0| < δ , выполняется неравенство |
|ϕ(x)| |
< |
|
|
ε |
. Для указанных x |
||||||||||||||||||||||||||||||||||||
c + 1 |
||||||||||||||||||||||||||||||||||||||||||
имеем |
| |
f |
( |
x |
) · |
ϕ |
x |
)| 6 |
c |
|
|
|
ε |
|
< ε. Поэтому |
lim f(x) |
· |
ϕ(x) = 0, и функция |
f(x) |
· |
ϕ(x) |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
· c + 1 |
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
бесконечно мала при |
x → x0. Теорема доказана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Замечание. |
|
В |
качестве |
примера |
на применение |
|
теоремы о связи функции, |
||||||||||||||||||||||||||||||||||
ее предела и бесконечно малой дадим другое доказательство |
утверждения |
о |
пре- |
|||||||||||||||||||||||||||||||||||||||
деле частного двух |
функций. |
Поскольку |
|
lim f(x) |
= |
|
a |
|
|
и |
lim g(x) |
= |
b, |
то |
||||||||||||||||||||||||||||
f(x) = a + ϕ(x) и g(x) = b + ψ(x), где ϕ(x) и ψ(x) − бесконечно малые при x → x0. При
этом b 6= 0, и g(x) = b + ψ(x) 6= 0 в некоторой проколотой окрестности точки |
x0. Чтобы |
|||||||||||||||||||
доказать равенство |
lim |
f(x) |
= |
a |
достаточно убедиться в том, что разность |
|
f(x) |
a |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
b |
|
|
g(x) |
− b |
|||||||||||||
|
x→x0 |
g(x) |
|
|
|
|
|
|
|
|
||||||||||
бесконечно мала при |
x → x0. Имеем |
|
|
|
|
|
|
|
||||||||||||
|
f(x) a |
= |
a + ϕ(x) |
|
a |
= |
bϕ(x) − aψ(x) |
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
g(x) − b |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
b + ψ(x) − b |
b(b + ψ(x)) |
|
|
|
|
|
|||||||||
Из теорем о произведении бесконечно малой величины на ограниченную и о сумме бесконечно малых следует, что функция, находящаяся в числителе последней дроби бесконечно мала (при x → x0). Далее, lim b(b+ψ(x)) = b2 — это следует из упомянутой выше
теоремы о связи функции, |
её предела и бесконечно малой. Поэтому для положительного |
||||||||||||||||||||||||||||||||
числа |
|
b2 |
|
|
найдется δ > 0 |
такое, что при |
0 < |x − x0| < δ выполняется неравенство |
||||||||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
b2 |
|
|
|
|
|
|
|
|
|
b2 |
|
||||||
|
|
|
|
|
|
|
|
|b(b + ψ(x)) − b2| < |
|
, т.е. − |
|
< b(b + ψ(x)) − b2 |
< |
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
Отсюда |
|
|
b(b + ψ(x)) > |
|
|
, и 0 < |
|
< |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
b2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b(b + ψ(x)) |
|
|
|
|
|
|
|
|
|
||||||||
|
Мы видим, что при 0 |
< |x − x0| < δ функция |
|
|
|
|
1 |
|
|
|
ограничена. Следо- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
b(b + ψ(x)) |
|||||||||||||||||||||||||||||||
вательно, |
|
|
bϕ(x) − aψ(x) |
|
есть произведение бесконечно малой (находящейся в числи- |
||||||||||||||||||||||||||||
|
b(b + ψ(x)) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
теле) на ограниченную функцию. |
Поэтому разность |
|
|
f(x) |
a |
бесконечно мала при |
|||||||||||||||||||||||||||
|
|
|
− |
|
|
||||||||||||||||||||||||||||
|
|
g(x) |
b |
||||||||||||||||||||||||||||||
|
→ |
0 |
|
|
|
, |
|
|
x→x0 |
|
g(x) |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
|
x |
, и |
|
следовательно, |
lim |
|
f(x) |
= |
a |
. |
Требуемое утверждение доказано. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2

Функция f(x), определённая в некоторой проколотой окрестности точки x0, называ-
ется бесконечно большой при x → x0, если lim |f(x)| = +∞. Аналогично определяются
x→x0
бесконечно большие функции и при других предельных переходах.
Теорема (о связи между бесконечно большой и бесконечно малой). Пусть функция
ϕ(x) отлична от нуля в некоторой проколотой окрестности точки x0. Эта функция бес-
1
конечно мала при x → x0 тогда и только тогда, когда функция f(x) = ϕ(x) является
бесконечно большой (при x → x0).
Доказательство. Необходимость. Пусть ϕ(x) бесконечно мала при x → x0, и пусть задано (сколь угодно большое) положительное число E. Возьмём столь малое ε > 0,
что ε < |
1 |
; тогда |
1 |
> E. Т.к. ϕ(x) бесконечно мала при x → x0, то существует |
|
E |
ε |
|
|||
δ = δ(ε) > 0 такое, что при всех x, 0 < |x − x0| < δ, выполняется неравенство |ϕ(x)| < ε. По условию теоремы ϕ(x) отлична от нуля в проколотой окрестности точки x0; отсюда
f(x) |
= |
1 |
|
> |
1 |
|
|
|
, и f(x) явля- |
|
|
ϕ(x) |
|
ε > E, т.е. f(x) > E. Поэтому f(x) → +∞ при x → x0 |
|||||||
ется| |
|бесконечно |
|
большой при|указанном| |
предельном| |
переходе| |
. Необходимость доказана. |
||||
Достаточность |
доказывается аналогично. Теорема доказана. |
|
||||||||
3

кафедра «Математическое моделирование» проф. П. Л. Иванков
Математический анализ
конспект лекций
для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)
Лекция 8.
Сравнение функций при данном стремлении аргумента. Эквивалентные бесконечно малые и бесконечно большие функции. Теоремы об эквивалентных функциях. Таблица эквивалентных бесконечно малых функций и её применение к вычислению пределов. Относительный порядок малости (или роста) функции при данном стремлении, выделение ее главной части. Теорема о сумме бесконечно малых разных порядков.
ОЛ-1, пп. 10.1-10.3
Пусть бесконечно малые при x → x0 функции ϕ(x) и ψ(x) отличны от нуля в некоторой
проколотой окрестности точки x0. Если lim ϕ(x) = 0, то говорят, что бесконечно малая
x→x0 ψ(x)
ϕ(x) имеет более высокий порядок малости по сравнению с ψ(x), а ψ(x) имеет более низкий порядок малости по сравнению c ϕ(x). Записывают это так: ϕ(x) = o(ψ(x)), x → x0. Последняя запись служит лишь для обозначения указанного соотношения между беско-
нечно малыми. |
Привычные свойства равенств могут при этом нарушаться. |
Например, |
|||||||
очевидно, x2 = o(x) и x3 |
= o(x) при x → 0. Отсюда, однако, не следует, что x2 = x3. Если |
||||||||
lim |
ϕ(x) |
|
то lim |
ψ(x) |
= 0, и на этот раз функция ψ(x) имеет при x |
|
x |
|
более |
ψ(x) = ∞, |
|
→ |
0 |
||||||
x→x0 |
x→x0 |
ϕ(x) |
|
|
|||||
высокий порядок малости по сравнению с ϕ(x).
Если существует конечный отличный от нуля предел lim ϕ(x) = C, то говорят,
x→x0 ψ(x)
что ϕ(x) и ψ(x) являются при x → x0 бесконечно малыми одного порядка и пишут ϕ(x) = O(ψ(x)), обязательно указывая, при каком предельном переходе имеет место это
соотношение (в данном случае при x → x0). В случае C = 1, т.е. если lim ϕ(x) = 1,
x→x0 ψ(x)
функции ϕ(x) и ψ(x) называют эквивалентными бесконечно малыми и пишут ϕ(x) ψ(x), x → x0. Если при x → x0 не существует ни конечного, ни бесконечного предела отношения
ϕ(x)
ψ(x), то говорят, что ϕ(x) и ψ(x) не сравнимы при x → x0.
Примеры. 1. При x → 0 имеем 1 − cos x = o(x), т.к.
lim 1 − cos x = lim
x→0 x x→0
2 sin2 |
x |
|
2x · sin2 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
sin2 |
x |
|
||||||
|
|
|
|
|
1 |
|
|
|
lim |
|
|
|
|||||||||||||
2 |
lim |
2 |
|
· |
lim x |
· |
2 |
= 0 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
|
= |
2 |
|
|
||||||||||||||||||
|
= x 0 |
4 · |
x |
|
2 |
x |
|
0 |
x |
|
0 |
|
x |
|
2 |
|
|||||||||
|
|
→ |
|
|
|
|
|
|
|
|
→ |
|
|
|
→ |
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||
1
√√
2. Функции ϕ(x) = |
2 + x2 − |
2 |
и ψ(x) = x2 являются бесконечно малыми одного порядка |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
→ |
|
|
|
x 0 |
|
x2 |
√2 |
x 0 2 √ |
x2 |
2 √ |
|
|
√ |
|||||||||||||
при x |
|
|
|
0, т.к. lim |
√2 + x2 − |
= lim |
|
|
|
|
|
|
= |
|
1 |
|
. Отсюда следует, что |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
√ |
|
|
|
|
√ |
|
|
→ |
|
|
|
|
|
|
→ x ( 2 + x + 2) |
|
2 2 |
|||||||||||
|
|
|
|
|
|
x2 |
при x → 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 + x |
|
− |
2 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
22
3.Бесконечно малые при x → 0 функции ϕ(x) = x и ψ(x) = x arctg x1 не сравнимы при
указанном предельном переходе, т.к. |
ψ(x) |
= arctg |
1 |
не имеет ни конечного, ни бесконеч- |
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
ϕ(x) |
|
x |
|
|
|
|
|
|
|
||||||
ного предела при x |
→ 0. |
В самом деле |
, |
lim arctg |
1 |
|
= |
π |
, |
lim arctg |
1 |
= |
− |
π |
. |
|||
|
|
|
x |
2 |
||||||||||||||
|
|
|
x 0+ |
x 2 |
|
x 0 |
|
|
||||||||||
|
|
|
|
|
→ |
|
|
|
|
|
|
→ − |
|
|
|
|
|
|
Рассмотрим некоторые теоремы о бесконечно малых функциях.
Теорема (о транзитивности отношения эквивалентности бесконечно малых). От-
ношение эквивалентности бесконечно малых (как и всякое отношение эквивалентности) обладает свойствами рефлексивности, т.е. ϕ(x) ϕ(x), симметричности, т.е. если ϕ(x) ψ(x), то ψ(x) ϕ(x), и транзитивности, т.е. если ϕ(x) ψ(x), а ψ(x) η(x), то ϕ(x) η(x); везде x → x0.
В доказательстве здесь нуждается лишь последнее свойство. Пусть функции ϕ(x),
ψ(x) и η(x) определены и отличны от нуля в некоторой проколотой |
окрестности точки |
|||||||||||||||||||||
x |
|
и бесконечно малы при x |
→ |
x |
. По условию lim |
ϕ(x) |
= |
lim |
ψ(x) |
= 1. Тогда |
||||||||||||
|
|
|
||||||||||||||||||||
|
0 |
|
ϕ(x) |
|
ϕ(x) |
ψ(x) |
|
0 |
|
|
x→x0 |
ψ(x) |
x→x0 η(x) |
|||||||||
lim |
= lim |
= 1, т.е. ϕ(x) |
|
η(x) при x |
|
|
x |
. Теорема доказана. |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
η(x) |
|
ψ(x) · |
|
|
→ |
|||||||||||||||||
x→x0 |
x→x0 |
η(x) |
|
|
|
|
0 |
|
|
|
|
|
||||||||||
Теорема (о необходимом и достаточном условии эквивалентности бесконечно ма-
лых). Бесконечно малые ϕ(x) и ψ(x) эквивалентны (при x → x0) тогда и только тогда, когда их разность имеет более высокий порядок малости при x → x0 по сравнению с каждой из них.
Доказательство. Необходимость. Пусть ϕ(x) ψ(x) при x → x0. Требуется до-
казать, что разность ϕ(x) − ψ(x) имеет более высокий порядок малости при x → x0 по сравнению с каждой их функций ϕ(x) и ψ(x). По определению эквивалентных бесконечно
малых имеем lim ϕ(x) = 1; по теореме о связи функции, её предела и бесконечно малой
x→x0 ψ(x)
выполняется равенство |
ϕ(x) |
|
= 1 + ε(x), ε(x) |
→ |
0 при x |
→ |
x |
. Отсюда |
ϕ(x) − ψ(x) |
= ε(x). |
|
ψ(x) |
ψ(x) |
||||||||||
|
|
|
0 |
|
|
||||||
Т.к. ε(x) – бесконечно малая при x → x0, то ϕ(x) − ψ(x) = o ψ(x) , x → x0. Аналогично
|
|
|
|
|
|
|
|
|
|
|
можно показать, что ϕ(x) − ψ(x) = o ϕ(x) |
при x → x0. Необходимость доказана. |
|||||||||
|
− |
|
|
|
→ |
0 |
|
|
ψ(x) |
|
Достаточность. Пусть ϕ(x) |
|
ψ(x) = o ψ(x) , x |
|
x |
. |
Тогда |
ϕ(x) − ψ(x) |
= o(1), и |
||
|
|
|
||||||||
ϕ(x)
ψ(x) = 1 + o(1), x → x0. Через o(1) обозначают бесконечно малую величину, характер
стремления которой к нулю неизвестен или не представляет интереса. Из последнего равенства следует, что ϕ(x) ψ(x) при x → x0. К такому же выводу можно прийти,
2
рассматривая равенство ϕ(x) −ψ(x) = o ϕ(x) , x → x0. Достаточность доказана. Теорема доказана.
Теорема (об использовании эквивалентных бесконечно малых при вычислении преде-
лов). Пусть f(x) и g(x) — бесконечно малые при x → x0 функции, отличные от нуля в некоторой проколотой окрестности точки x0, и пусть f(x) ϕ(x) при x → x0. Тогда, если
существует предел lim |
ϕ(x) |
= A, то существует и предел lim |
f(x) |
также равный A. |
|||||||||||||
|
g(x) |
||||||||||||||||
x→x0 |
g(x) |
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
||||
Доказательство. Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
f(x) |
= |
lim |
ϕ(x) |
· |
f(x) |
lim |
ϕ(x) |
= A , |
|
|||||||
g(x) |
g(x) |
ϕ(x) |
|
|
|||||||||||||
x x0 |
|
x |
→ |
x0 |
= x |
→ |
x0 |
g(x) |
|
|
|||||||
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.к. lim f(x) = 1. Теорема доказана.
ϕ(x)
Заметим, что при вычислении предела произведения бесконечно малых сомножители также можно заменять на эквивалентные.
Пусть теперь f(x) и g(x) — бесконечно большие функции при x → x0. Говорят, что
эти функции являются бесконечно большими одного порядка (при x → x0) если |
|
||||
lim |
f(x) |
= C , |
(1) |
||
g(x) |
|
||||
x→x0 |
|
|
|||
Где C — отличное от нуля число. При этом пишут f(x) = O g(x) , x → x0. При C = 1 бесконечно большие f(x) и g(x) называют эквивалентными и пишут f(x) g(x), x → x0. Если в (1) число C равно нулю, то говорят, что g(x) есть бесконечно большая более высокого порядка роста по сравнению с f(x) (а f(x) есть бесконечно большая более низкого
порядка роста по сравнению с g(x)) и пишут f(x) = o g(x) , x → x0. Для бесконечно больших справедливы аналоги доказанных выше теорем (кроме теоремы о необходимом и достаточном условии эквивалентности бесконечно малых). Как обычно, все рассматриваемые понятия и теоремы можно распространить и на другие предельные процессы (включая односторонние пределы).
Пусть ϕ(x) и ψ(x) бесконечно малые при x → x0. Если при некотором k бесконечно малые ϕ(x) и ψ(x) k являются бесконечно малыми одного порядка, то говорят, что ϕ(x)
k
имеет порядок малости k по сравнению с ψ(x) при x → x0. Если ϕ(x) A ψ(x) , где A 6= 0 — некоторое число, то ϕ(x) = A ψ(x) k +o (ψ(x))k , x → x0. В этом случае говорят,
что выделена главная часть вида A ψ(x) k бесконечно малой ϕ(x). Определение порядка малости и выделение главной части не всегда возможно. В качестве ψ(x) для выделения главной части обычно выбирают более простую (или лучше изученную) бесконечно малую.
1
Например, если x → x0, то часто берут ψ(x) = x−x0, а если x → ∞, то полагают ψ(x) = x.
Аналогичные понятия вводятся и для бесконечно больших функций. Пусть f(x) и g(x) — бесконечно большие при x → x0 функции. Говорят, что f(x) имеет порядок роста k по
k
сравнению с g(x), если f(x) и g(x) имеют одинаковый порядок роста при x → x0. Если A — ненулевое число, и f(x) = A g(x) k + o (g(x))k , x → x0, то говорят, что у бесконечно большой функции f(x) выделена главная часть вида A g(x) k. При x → x0 обычно берут
1
g(x) = x − x0 , а при x → ∞ полагают g(x) = x. Как и в случае бесконечно малых выделение главной части (и определение порядка роста) не всегда возможно.
Примеры. 1. Функции ϕ(x) = arccos x и ψ(x) = 1 − x бесконечно малы при x → 1−
(для ψ(x) это очевидно; равенство lim arccos x = 0 уже рассматривалось выше). Опреде-
x→1−
3

лим порядок малости ϕ(x) относительно ψ(x). Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
lim |
|
arccos x |
= |
lim |
arccos cos t |
= lim |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||||
|
|
(1 |
|
cos t)k |
1 − |
1 − |
|
|
|
|
t |
|
k |
|
|
|
|
|
|
||||||||||||||||||||
x 1 |
(1 |
− |
x)k |
t 0+ |
− |
t |
→ |
0+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
→ − |
|
|
|
|
→ |
|
|
|
|
|
|
|
2 sin2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
t |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→0+ 2k |
· sin2k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
Ясно, что конечный отличный от нуля предел получается лишь при k = |
1 |
. |
При этом |
||||||||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||||||||
значении k имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
arccos x |
|
|
|
|
|
|
t |
|
|
|
= √ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
lim |
= lim |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
→ |
− |
√ |
1 − x |
|
|
|
→ |
|
√2 · sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
t |
|
0+ |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для раскрытия последней неопределённости мы воспользовались теоремой о первом за-
мечательном пределе. |
Итак, ϕ(x) |
= arccos x есть бесконечно малая порядка 1/2 |
по |
|||||||||||||||||||||||||
сравнению с ψ(x) = 1 − x при x → 1−. |
|
Из наших вычислений следует также, |
что |
|||||||||||||||||||||||||
1 |
|
x , |
p, |
|
|
√ |
|
|
x) |
|
1 |
|
x , arccos x = |
1 x |
|
+ o( |
1 |
|
x ), x |
|
1 . |
|||||||
|
|
|
2(1 |
|
|
|
|
|
|
|||||||||||||||||||
arccos x = |
2(1 − x) + o( 1 − x), x → 1−. |
Если в качестве |
ψ(x) |
взять бесконечно малую |
||||||||||||||||||||||||
√ |
|
− |
2 |
|
то |
поскольку |
|
|
|
− |
|
|
√ |
|
− |
2 |
√ |
− |
2 |
|
√ |
|
− |
2 |
|
→ |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
задач это равенство может оказаться удобнее предыдущего |
|
|||||||||||||||||||
При решении некоторыхp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||||||
2. Пусть a > 1, и пусть f(x) = ax, g(x) = x. В дальнейшем будет доказано, что при любом
k имеет место равенство lim ax = ∞. Поэтому нельзя определить порядок роста f(x)
x→+∞ xk
относительно g(x); нельзя также выделить у функции f(x) главную часть вида A · xk при x → +∞.
Теорема (о сумме бесконечно малых разных порядков). Пусть ϕ1(x), . . . , ϕn(x), ψ(x)
— бесконечно малые при x → x0 функции, и пусть ki — порядок малости функций ϕi(x) относительно ψ(x), i = 1, . . . , n, причём числа k1, . . . , kn попарно различны. Тогда сумма ϕ1(x) + . . . + ϕn(x) эквивалентна при x → x0 слагаемому минимального порядка относительно ψ(x).
Доказательство проведём по индукции. При n = 1 нечего доказывать. Пусть при некотором n > 1 утверждение теоремы справедливо, и пусть даны бесконечно малые ϕ1(x), . . . , ϕn(x), ϕn+1(x), ψ(x), удовлетворяющие условиям теоремы. Пусть (для определённости) kn+1 — минимальное среди чисел k1, . . . , kn, kn+1, а kn — минимальное среди чисел k1, . . . , kn. Тогда по предположению индукции ϕ1(x) + . . . + ϕn(x) ϕn(x), x → x0.
Далее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= x→x0 |
|
|
|
|
|
|
+ 1 |
|
|
|
|
||||||||
x→x0 |
|
|
|
|
|
|
|
ϕn+1(x) |
|
|
|
|
|
ϕn+1(x) |
|
|
|
|
|
|
|
|||||||||||||||||
lim |
ϕ1(x) + . . . + ϕn(x) + ϕn+1(x) |
|
|
lim |
|
ϕ1(x) + . . . + ϕn(x) |
= |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕn(x) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 + lim |
= 1 + lim (ψ(x))kn−kn+1 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕn+1(x) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
|
|
x→x0 |
|
|
|||||||
Последний предел равен нулю, т.к. |
|
ψ(x) |
kn−kn+1 → 0 при kn |
> kn+1. |
Таким образом, |
|||||||||||||||||||||||||||||||||
ϕ1(x) + . . . + ϕn(x) + ϕn+1(x) ϕn+1(x) при x → x0, и по индукции теорема доказана. |
||||||||||||||||||||||||||||||||||||||
Аналогичная теорема справедлива и для бесконечно больших функций: сумма беско- |
||||||||||||||||||||||||||||||||||||||
нечно больших различных порядков эквивалентна слагаемому наивысшего порядка. |
||||||||||||||||||||||||||||||||||||||
Пример |
|
|
|
Если |
|
|
|
|
то |
|
2 |
|
|
√ |
|
2 |
|
|
2 |
√ |
|
√3 |
|
2 |
|
поэтому |
||||||||||||
. |
|
|
|
|
|
x |
|
|
|
, 2x |
|
x |
; |
|||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
x → +∞2 , |
|
|
|
|
+ x + x |
x |
|
+ x + |
2x |
|
|||||||||||||||||
|
x |
+ x + |
√x |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
xlim |
|
|
√ |
|
|
√3 |
|
|
= xlim |
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
→∞ 2x |
|
|
+ x + |
→∞ 2x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Мы пока не располагаем общими методами выделения главной части, поэтому более подробно на этом способе вычисления пределов не останавливаемся.
4
кафедра «Математическое моделирование» проф. П. Л. Иванков
Математический анализ
конспект лекций
для студентов 1-го курса 1-го семестра всех специальностей ИУ, РЛ, БМТ (кроме ИУ9)
Лекция 9.
Непрерывность функции в точке: равносильные определения. Непрерывность суммы, произведения, композиции непрерывных функций. Свойства функций, непрерывных в точке. Односторонняя непрерывность функции. Непрерывность функции на промежутке (на интервале, полуинтервале и отрезке). Непрерывность основных элементарных функций (док-во для многочлена и синуса). Точки разрыва функций, их классификация.
ОЛ-1, пп. 9.1-9.3
Пусть X R, и пусть на X задана числовая функция f(x). Эта функция называется непрерывной в точке x0 X, если для любого ε > 0 существует число δ = δ(ε) > 0 такое, что при всех x, |x − x0| < δ, выполняется неравенство |f(x) − f(x0)| < ε. Если x0 — изолированная точка множества X (т.е у этой точки имеется окрестность, не содержащая точек множества X, отличных от x0), то в соответствии с этим определением функция f(x) непрерывна в точке x0. Например, последовательность {xn}, являющаяся, как известно, функцией натурального аргумента, непрерывна в каждой точке области своего определения (здесь для произвольного ε > 0 можно взять δ = 1/2). Такая «непрерывность» интереса не представляет. Мы будем, в основном, применять понятие непрерывности к функциям, заданным на промежутках. Пусть I — промежуток, f: I → R, и пусть x0 I, причём x0 является внутренней точкой этого промежутка. Очевидно, непрерывность функции f(x) в точке x0 означает, что lim f(x) = f(x0). Это равенство в
рассматриваемом случае можно принять за определение непрерывности функции f(x) в точке x0. Рассмотрим другой подход к определению непрерывности функции. Пусть снова x0 — внутренняя точка промежутка I, на котором задана числовая функция f(x). Если x0 I, то приращением аргумента называют разность x = x − x0; соответствующим приращением функции называют f(x0) = f(x) − f(x0) = f(x0 + x) − f(x0). Нетрудно проверить, что для непрерывности функции f(x) при x = x0 необходимо и достаточно, чтобы выполнялось равенство
lim f(x0) = 0 . |
(1) |
x→0 |
|
В самом деле, если функция f(x) непрерывна при x = x0, то для любого ε > 0 существует число δ = δ(ε) > 0 такое, что при всех x, |x − x0| < δ, т.е. при | x| < δ, выполняется неравенство |f(x) − f(x0)| < ε, т.е. | f(x)| < ε. Это означает выполнение соотношения
(1). Таким образом, условие (1) необходимо для непрерывности функции f(x) в точке x0. Если же выполнено условие (1), то для любого ε > 0 существует δ = δ(ε) > 0 такое,
1
