Matanaliz

1. Если каждому значения переменной xЄ{x} ставится соответствие по определённому закону числу yЄ{y}, то говорят, что на {x} задана функция y=f(x). Способы задания функции: словесный, аналитический (с помощью формул и станд. значений), графический (с помощью графика), табличный. Основные элементарные функции: степенная у=хⁿ, показательная у=а^х, а>0, логарифмическая у=log_ax, а>0; тригонометр. ф-ии y=sinx, y=cosx, y=tgx, y=ctgx, y=secx, y=cosecx; обратные тригоном. ф-ии y=arcsinx, y=arccosx, y =arctgx, y=arcctgx.

2. Пусть x=ψ(t) задана на {t}, а y=f(x) задана на множестве значений предыдущих ф-ий {x}, тогда говорят, что на множестве {t} определена сложная ф-ия y=f[ψ(t)]=F(t). t-независимый аргумент, x-промежуточный. (…). Функции, заданные одной формулой посредством конечного числа арифметических действий и операций, определяемых основными элементарными функциями, наз-ся элементарными.

3. Если каждому натур. числу 1,2,3… ставится в соответствии по опр. закону число х₁, х₂, х₃…, то говорят, что задана числовая последовательность: {x_n}=x₁, x₂, x₃… (пр: {1/n}=1, ½, ⅓, ¼ …). Последовательность {x_n} наз-ся сходящайся, если для неё существует число а такое, что для любого ξ>0 сущ. N(ξ), что при n>N(ξ) будет выполнятся |x_x-a|<ξ. lim x_n=a(n→∞). a – предел последовательности. (пр: {n/n+2}=⅓, ½ , 3/5, 2/3…; a=1; lim n/n+2=1 (n→∞); |x_n-a|=|n/(n+2) -1|=|-2/n+2|=2/n+2<ξ; ξ=3; 2/n+2<3 при n≥1; n+2/2>1/ξ; n+2>2/ξ; n>2/ξ-2; N(ξ)=[2/ξ-2]).

4. {x_n} и {y_n}; {x_n}+{y_n}={x_n+y_n}; {x_n}-{y_n}={x_n-y_n}; {x_n}∙{y_n}={x_n∙y_n}; {x_n}/{y_n}={x_n/y_n} y_n≠0 при любом n.

5. Последовательность {x_n} наз-ся сходящайся, если для неё существует число а такое, что для любого ξ>0 сущ. N(ξ), что при n>N(ξ) будет выполнятся |x_x-a|<ξ. lim x_n=a(n→∞). a – предел последовательности. Св-ва: 1) Если последовательность сходится, то она имеет есдинст. предел. Док-во: {x_n} – сходится. Предположим, что пос-ность имеет два предела неравные друг другу. lim x_n=a (n→∞), lim x_n=b (n→∞), a≠b; по опр.: при n>N₁(ξ);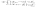

при n>N₂(ξ); b-a≠0; ξ=(b-a)/4>0; N(ξ)=max{N₁,N₂}; неравенство * будет выполняться при n>N; |b-a|=|x_n-a+b-x_n|≤ | x_n-a|+| x_n-b|<ξ+ξ=2ξ; при n>N; |b-a|<2∙|b-a|/4; |b-a|>0. Противоречие, предположение неверно =>a=b. 2) Сходящ. пос-ность является ограниченной. Док-ко: lim x_n=a (n→∞), a-конечное число. Любое ξ>0; |x_n-a|<ξ; ξ <x_n-a<ξ; a-ξ< x_n<a+ξ; A=max{| x₁-a|,| x₂-a|,…| x_n-a|,ξ}=>| x_n-a|≤A; a-A≤ x_n≤A+a это означает, что пос-ность ограничена.

6. Числ. пос-сть наз-ся бесконечно большой ч.п., если для любого А>0 сущ. N(A), что |x_n|>A при n>N(A); lim x_n =∞ (n→∞). ЧП наз-ся бесконечно малой ЧП, если она сходится и имеет предел, равный нулю. lim α_n=0 (n→∞), α_n – б.м.ч.п. (пр: {1/n} – б.м.ч.п.; {0} = 0,0,0,0…-бмчп; {1/n²}=1, ¼ , 1/9, 1/16, -бмчп.). Числ. пос-сть наз-ся ограниченной, если ограничено множество значений этой последовательности. {x_n}= x₁, x₂, x₃,… x_n; m≤ x_n≤M; a< x_n<b; | x_n|<A (пр: {n/(n+1)}= ½ , 2/3, ¾ ; 0<n/(n+1)<1. Если пос-ность является бесконечно большой, то она является неограниченной, а обратное утверждение вообще неверно.

7. {x_n} - сходящаяся последовательность и a ее предел. |x_n-a|<ξ при n>N; a−ξ<x_n<a+ξ при n>N; Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ξ∣,∣a+ξ∣, ∣  x₁∣ , ∣  x2∣ ,...,∣ х_N−1 ∣. { x_n}<A => пос-ность ограничена.

8. Если последовательность сходится, то она имеет есдинст. предел. Док-во: {x_n} – сходится. Предположим, что пос-ность имеет два предела неравные друг другу. lim x_n=a (n→∞), lim x_n=b (n→∞), a≠b; по опр.: при n>N₁(ξ);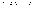

при n>N₂(ξ); b-a≠0; ξ=(b-a)/4>0; N(ξ)=max{N₁,N₂}; неравенство * будет выполняться при n>N; |b-a|=|x_n-a+b-x_n|≤ | x_n-a|+| x_n-b|<ξ+ξ=2ξ; при n>N; |b-a|<2∙|b-a|/4; |b-a|>0. Противоречие, предположение неверно =>a=b.

9. Произведение бесконечно малой ЧП на ограниченную есть бесконечно малая ЧП. lim α_n=0 (n→∞); {n_n}:|x_n|<A при любом n; { α_n}∙{x_n} = { α_n∙x_n}. Доказать, что пос-ность бесконечно малая. | α_n∙x_n-0|=|α_n∙x_n|; любое ξ>0 =>ξ₁=ξ/A; A>0, тогда|α_n∙x_n|<ξ₁A при n>N(ξ₁); |α_n∙x_n|<ξ/A∙A=ξ; n>N; lim α_n∙x_n=0 (n→∞). (Пр: {cos n/n} ={cos n}∙{1/n}; |cos n|<2; lim1/n =0 => lim cosn/n =0 (n→∞).

10. Если элементы сходящейся последовательности {x_n}, начиная с некоторого номера, удовлетворяют неравенству  x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b). x_n ≥ b, доказать, что a ≥ b. Предположим, что a < b. ξ=b-a сущ. N при n>N выполняется |x_n - a| < b – a;  a-b < x_n - a < b – a; x_n<b это противоречит условию. Теорема доказана. Следствие 1. Если элементы x_n и y_n сходящихся последовательностей {x_n} и {y_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≤ y_n, то их пределы удовлетворяют такому же неравенству:

  В самом деле, элементы последовательности {y_n - x_n} неотрицательны, а поэтому неотрицателен и ее предел . Отсюда следует, что . Следствие 2. Если все элементы сходящейся последовательности {x_n} находятся на сегменте [a, b], то и ее предел c также находится на этом сегменте. В самом деле, так как a ≤ x_n ≤ b, то a ≤ c ≤ b.

11. Всякая функция f (х), непрерывная на отрезке [а, b], принимает на этом отрезке свое наименьшее и наибольшее значения, т. е. на отрезке[ a, b] существуют такие точки х₁, x₂, что для любого х О [а, b] выполняются неравенства

f(х₁)<=f(x)<=f( x₂) (…)

12. Определение предела ф-ии при x→a по Коши, а – конечное число. Число b называется пределом ф-ии y=f(x) при x→a, если для любого ξ>0 существует δ(ξ)>0 такое, что |f(x)-b|<ξ; при 0<|x-a|<δ(ξ). lim f(x)=b (x→a). По Гейне: Число b наз-ся пределом ф-ии y=f(x) при x→a, если для любой {x_n}:lim x_n=a (n→∞), x_n≠a, то соответствующая пос-ность значений ф-ии {f(x_n)} сходится к b, т.е. lim f(x_n)=b (n→∞). Определения по Коши и по Гейне эквиваленты. Смысл обоих определений: чем ближе значения аргумента x к числу a, тем ближе значение y к числу b. Замечание: предел точки может не существ. или может быть равен бесконечности, тогда ф-ия наз-ся бесконечно большой.

13. Число А наз-ся пределом ф-ии f(x) при x→∞, если для любого ξ>0 существует такое число M>0, что как только |x|>M, выполняется |f(x)-A|<ξ.

14. Если ф-ия f(x) стремиться к некоторому числу B₁, при этом аргументы будут x<a, тогда, если выполняется условие предела ф-ии, говорят, что B₁ наз-ся левосторонним пределом ф-ии или пределом слева. lim f(x)=B₁ (x→a-0). Если ф-ия f(x) стремиться к B₂ и при этом x>a, тогда предел наз-ся правосторонним пределом или пределом ф-ии справа. lim f(x)=B₂ (x→a+0)

15. Ф-ия y=f(x) наз-ся ограниченной, если существует такое положительное число М, что для всех x из области определения ф-ии значение |f(x)|<M. Ф-ия f(x) наз-ся ограниченной при x→a, если существует окрестность точки а, в которой ф-ия f(x) ограничена. Ф-ия y=f(x) наз-ся ограниченной при x→∞, если существет такое число N>0, что как только |x|>N, ф-ия становиться ограниченной.

16. Ф-ия y=f(x) наз-ся бесконечно малой при x→a, если lim f(x) =0 (x→a).

17. Теорема об арифмет. операциями над функциями, имеющие конечные пределы в данной точке. Если lim f(x)=b и lim ψ(x)=c (x→a), то lim (f(x)-ψ(x))=b-c (x→a); lim (f(x)∙ψ(x))=b∙c; lim (f(x):ψ(x))=b:c (c≠0). Док-во: для произведения. Используем определение предела по Гейне. {x_n}:lim x_n=a (n→∞); x_n≠a, по условию теоремы lim f(x_n)=b, lim ψ(x_n)=c (n→∞). Согласно свойству ч.п., lim (f(x)∙ψ(x))=b∙c (n→∞), а это означает, что lim (f(x)∙ψ(x))=b∙c (x→a)

18. 1) Пусть в некоторой окрестности x=a выполняется φ(x)≤f(x)≤ψ(x). lim φ(x)=b, lim ψ(x)=b (x→a)=>(*из двух пределов следует) lim f(x)=b. Док-во по Коши: | φ(x)-b|<ξ при 0<|x-a|<δ₁; | ψ(x)-b|<ξ при 0<|x-a|<δ₂ (под фигурной скобкой два модуля). δ=min{δ₁;δ₂}. Оба неравенства * будут выполняться при 0<|x-a|<δ; -δ< φ(x)-b<ξ; -ξ< ψ(x)-b<ξ; φ(x)-b≤f(x)-b≤ψ(x)-b из условия. –ξ<f(x)-b<ξ; |f(x)-b|<ξ при 0<|x-a|<δ. из определения предела по Коши следует, что lim f(x)=b (x→a). 2) Если в некоторой окрестности x=a f(x)≥0, lim f(x)=b (x→a), то b≥0 (f(x)>0=>b≥0). Если f(x) ≤0, то b≤0 (f(x)<0=>b≤0). 3) Если в некоторой окрестности x=a f(x)≤φ(x), lim f(x)=b (x→a); lim φ(x)=c (x→a), то b≤c. 4) f(x)≤φ(x); lim f(x)=+∞ (x→a) =>lim φ(x) =+∞ (x→a); lim f(x)=-∞ (x→a) => lim φ(x)=-∞ (x→a).

19. Функция f (x) называется бесконечно большой функцией в точке х = x₀ (или x → x₀), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х₀ | < δ , выполняется неравенство | f (x) | > К. lim f(x)=∞ (x→x₀).(…)

20. Функция f (x) называется бесконечно малой функцией в точке х = х₀, если lim f(x)=0 (x→x₀). Функция f (x) называется бесконечно большой функцией в точке х = x₀ (или x → x₀), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х₀ | < δ , выполняется неравенство | f (x) | > К. lim f(x)=∞ (x→x₀).(…)

21. Свойста (?). Сравнение: lim α(x)=0, lim β(x)=0 (x→a). a может быть конечным числом, а может быть бесконечным числом. 1. lim α(x)/ β(x)=c≠0 (x→a). α и β

б. м. одного порядка при x→a. lim sinx/x=1 (x→0). sin x и x б.м. ф-ии одного порядка. 2. lim α(x)/ β(x) =1(x→a). α и β эквивалентные б.м. при x→a. α(x)~β(x). Эквивалентные б.м. являются бесконечно малыми одного порядка. 3. а) lim α(x)/ β(x) =0 (x→a). α(x) является б.м. более выского порядка, чем β(x). α=о(β). lim sin²x/3x = lim (sinx/x) ∙ ((sinx)/3)=1∙0/3=0, sin²x=o(3x). б) lim α(x)/ β(x) =∞ (x→a)=> lim α(x)/ β(x) =0(x→a)=> β(x)=o(α(x)). 4. lim α(x)/ β(x) – не существует. б.м. ф-ии не сравниваемые.

22. Теор. 1. Для того, чтобы две бесконечно малые ф-ии α(х) и β(х) при (x→a) были эквивалентны, необходимо и достаточно, чтобы их разность быа бесконечно малой ф-ии более высокого порядка, чем любая из исходных. Док-во: 1) Необходимость. Дано: lim α(x)=0(x→a), lim β(x) =0(x→a), lim α(x)/ β(x) =1(x→a). γ(х)=α(х)-β(х). Очевидно, что lim γ(x)= 0 (x→a). lim γ(x)/α(x)=lim (α(x)-β(x))/α(x)=lim 1-β(x)/α(x)=1-1=0 (x→a).. γ(x)=o(α(x)), γ(x)=o(β(x)) аналогично. 2) Достаточность. γ(x)=o(α(x)), γ(x)=o(β(x)). lim (α(x)-β(x))/α(x) =0 (x→a). lim 1-β(x)/α(x)=0=>lim α(x)/β(x)=1=>α~β. Теор. 2 Если α(х) эквив. α₁(х) и β(х) эквив. β₁(х), то lim α(x)/β(x)=lim α₁(х)/β₁(х) (x→a). lim α(x)/β(x)=lim (αβ₁α₁)/(βα₁β₁)=lim (α/α₁)∙(β₁/β)∙(α₁/β₁)=lim α₁/β₁(x→a).

23. lim f(x)=∞, lim φ(x)=∞ (x→a). 1) lim f(x)/φ(x) =c≠0 (x→a) – ф-ии одного порядка. 2) lim f(x)/φ(x)=1 (x→a) – б.б. ф-ии асимптотически равны. 3) lim f(x)/φ(x) =0 (x→a). φ(x) –б.м. более высокого порядка, чем f(x), lim φ(x)/f(x)=∞. lim (2x²+x+1)/(3x+7x²) (x→∞) =(∞/∞)=∞. 2x²+x+1 – б.б. ф-ия более высокого порядка, чем 3x-7.

24. lim (sin x)/x=1 (x→0) первый замечательный предел. x→0+0; S_OBF<S_сегOBA<S_ODA; ½ sinx∙cosx< ½ ∙1²< ½ tgx. S_сег= ½ R²α. R=1. sinx>0; cox<x/sinx<1/cosx(*); 1/cosx>sinx/x>cosx. x→0-0. Равенство справедливо, т.к. все части неравенства являются чётными ф-иями. lim cosx=1 (x→0), lim 1/cosx=1 (x→0). Из (*) следует первый замечательный предел. Следствия первого замечательно предела: lim x/sinx=1 (x→0); Lim tgx/x=1 (x→0); lim arcsinx/x=1 (x→0); lim arctgx/x=1 (x→0). Второй замечательный предел lim (1+1/x)^x=e (x→∞). lim (1+1/)ⁿ=e (n→∞). x→+∞; n≤x<n+1; 1/(n+1)<1/x≤1/n; 1+1/(n+1)<1+1/x≤1+1/n; (1+1/(n+1))ⁿ≤(1+1/x)^x<(1+1/n)ⁿ⁺¹ (**). x→∞n→+∞; lim (1+1/(n+1))ⁿ=lim(1+1/(n+1))^n+1-1=lim e(1+1/(n+1))^-1=e (n→∞). lim (1+1/n)ⁿ⁺¹=lim e∙(1+1/n)¹=e (n→∞). Из (**) вытекает второй замечательный предел.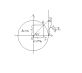

25. 1) Гиперболический синус: y=shx=(e^x-e^-x)/2 .

2) Гиперболический косинус y=chx=(e^x+e^-1)/2.

3) Гиперболический тангенс y=thx=shx/chx=(e^x-e^-x)/(e^x+e^-x)

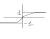
4) Гиперболический котангенс y=cthx=chx/shx=(e^x+e^-x)/(e^x-e^-x). Соотношение формулы для гиперболических ф-ий аналогичны формулы для тригонометрических ф-ий. sh2x=(e^2x-e^-2x)/2=((e^x)²-(e^-x)²/2=2(((e^x-e^-x)(e^x+e^-x))/2∙2)=2shx∙chx. ch²x-sh²x=1; ch²x+sh²x=ch2x.

26. Опр1. Ф-ия y=f(x) наз-ся непрерывной в точке x=a, если выполняется равенство lim f(x)=f(a) (x→a). Замечание: если ф-ия непрерывна в т. x=a, то она определена в некоторой окрестности точки, включая саму точку x=a; ф-ия имеет в данной точке конечный предел; предел ф-ии равен частному значению ф-ии в этой точке. Опр2. Ф-ия y=f(x) непрерывна в т. x=a, если для любого ξ>0 существ. δ(ξ), что |f(x)-f(a)|<ξ при |x-a|<δ(ξ). x-a=Δx приращение аргумента в т. x=a; f(x)-f(a)=Δy – приащение ф-ии в т. а. Опр. 3. Ф-ия y=f(x) непрерывна в т x=a, если lim Δy = 0 (Δx→0). опр 1,2,3 эквивалентны. При малых изменениях аргумента ф-ия изменяется незначительно. Смысл непрерывности из опр 3: при малых изменениях аргумента значение ф-ии меняется незначительно. Опр 4. Ф-ия наз-ся непрерывной на множестве {x}, если она непрерывна в каждой точке этого множества. Опр.5 ф-ия y=f(x) наз-ся непрерывной слева (справа), если lim f(x)=f(a) (x→a-0) (lim f(x)-f(a) (x→a+0)). lim arcsin x =-π/2 (x→-1+0), lim arcsin x =π/2 (x→1-0). Опр.6. Ф-ия y=f(x) наз-ся непрерывной на сегмента [a,b], если она непрерывна на (a,b), непрерывна в т. x=a справа и непрерывна в т. x=b слева.

27. Функция f (x) будет равномерно непрерывна на множестве {x} , если ∀ε >0, ∃δ=δ (ε ) >0, ∀x₁,x₂ ∈{x}:|x₁ –x₂| <δ ⇒|f(x₁)−f(x₂)| < ε. Теорема Кантора: Любая непрерывная на отрезке [a; b] функция – равномерно непрерывная. Док-во от обратного. Допустим, что f(x) непрерывная на [a,b], но не является равномерно непрерывной, т.е. ∃ε₀> 0, ∀δ, ∃x₁,x₂Є[a,b]< δ=>|f(x₁)-f(x₂)|>ξ₀ (…)

28. Все элементарные функции являются непрерывными в любой точке свой области определения. Функции, заданные одной формулой посредством конечного числа арифметических действий и операций, определяемых основными элементарными функциями, наз-ся элементарными. Такие как степенная у=хⁿ, показательная у=а^х, а>0, логарифмическая у=log_ax, а>0; тригонометр. ф-ии y=sinx, y=cosx, y=tgx, y=ctgx, y=secx, y=cosecx; обратные тригоном. ф-ии y=arcsinx, y=arccosx, y =arctgx, y=arcctgx. Используя определение непрерывности в терминах приращений, доказать, что функция непрерывна в произвольной точке x = a. Решение.Условие непрерывности по Гейне можно записать в виде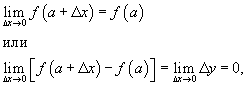

      

где Δx и Δy − малые приращения. Для заданной функции справедливы следующие соотношения в точке x = a:

      Следовательно,

 Вычислим предел.

  Таким образом, функция является непрерывной в произвольной точке x = a. 

29. Если f(x) и φ(x) непрерывны в т. x=a, то ф-ии f(x)+φ(x), f(x)∙φ(x), f(x)/φ(x) (φ(x)≠0) непрерывны в т. x=a. Док-во: lim f(x)=f(a) (x→a); lim φ(x)=φ(a) (x→a). По теореме об арифмет. операциями над ф-ями, имеющие конечные предельные значения, получаем : lim f(x)±φ(x)= f(a)±φ(a) (x→a). lim f(x)∙φ(x)= f(a)∙φ(a) (x→a)(*). lim f(x)/φ(x)= f(a)/φ(a) (x→a). (*) означает, что f(x)∙φ(x) имеет предел, равный частному значению ф-ии. По определению непрерывности ф-ия f(x)∙φ(x) непрерывна в т. x=a.

30. Если ф-ия y=f(x) непрерывна в т. x=a и f(a)≠0, то в некоторой окрестности x=a ф-ия сохраняет знак своего значения f(a). f(a)>0. По определению непрерывности ф-ии: |f(x)-f(a)|<ξ при |x-a|<δ(ξ); -ξ<f(x)-f(a)<ξ; f(a)-ξ<f(x)<ξ+f(a); ξ=f(a)/2>0; 0<f(a)/2<f(x)<3/2 ∙f(a). f(x)>0 при x-a|<δ(ξ), где ξ=f(a)/2. Если f(a)<0, то –f(a)>0. В некоторой окрестности x=a -f(x) положительна => f(x)<0 отрицательна в некоторой окрестности.

31. Если f(x) непрерывна на [a,b], строго монотонна и имеет область значений yЄ[α,β], то на [α,β] существует обратная непрерывная строго монотонная ф-ия, что x=f^-1(y), имеющая область значения [a,b].  (пример y=sin x. На [-π/2;π/2] выполняются все условия теоремы. yЄ[-1;1] ) Непрерывность сложной ф-ии: Если x=φ(t) непрерывна в т. t=a, а ф-ия y=f(x) непрерывна в т. x=b= φ(a), то сложная ф-ия y=f[φ(t)] непрерывна в т. t=a. Док-во: Возьмём последовательность ∀{t_n}; lim{t_n}=a; t_n≠a (n→∞) => lim f(t_n)=b= φ(a) (n→∞). В силу непрерывности φ(t_n) { φ(t_n)}={x_n}, x_n→b. В силу непрерывности y=f(x) limf(x_n)=f(b)=f[φ(a)] (n→∞). Используя опр. по Гейне: lim f[φ(t)]=f[φ(a)] (t→a) непрерывность ф-ии в т. a (пример: y=ln(sinx), u=sinx. u=sinx при xЄ(-∞;+∞). y=ln u непрерывна при u>0, sinx>0; 2πn+0<x<π+2πn.

32. Непрерывность сложной ф-ии: Если x=φ(t) непрерывна в т. t=a, а ф-ия y=f(x) непрерывна в т. x=b= φ(a), то сложная ф-ия y=f[φ(t)] непрерывна в т. t=a. Док-во: Возьмём последовательность ∀{t_n}; lim{t_n}=a; t_n≠a (n→∞) => lim f(t_n)=b= φ(a) (n→∞). В силу непрерывности φ(t_n) { φ(t_n)}={x_n}, x_n→b. В силу непрерывности y=f(x) limf(x_n)=f(b)=f[φ(a)] (n→∞). Используя опр. по Гейне: lim f[φ(t)]=f[φ(a)] (t→a) непрерывность ф-ии в т. a (пример: y=ln(sinx), u=sinx. u=sinx при xЄ(-∞;+∞). y=ln u непрерывна при u>0, sinx>0; 2πn+0<x<π+2πn.

33. Если ф-ия y=f(x) непрерывна во всх точках некоторой окрестности x=a, кроме самой точки x=a, где нарушается непрерывность, то x=a наз-ся точкой разрываф-ии. 1) y=f(x), x=a – точка разрыва. Если lim f(x)=b (x→a) – конечное число, то x=a – устранимая точка разрыва. (lim sinx/x=1 (x→0); y=( sinx/x x≠0; x=1 x=0) – непрерывна. 2) limf(x)=b (x→a-0), lim f(x)=c (x→a+0), b≠c. b,c – конечные числа. Тогда x=a –точка разырва первого рода. y=sgnx; x=0 точка разрыва первого рода. 3) lim f(x) (x→a±0) – не существует или равен ∞, то x=a точка разырва второго рода.

34.

35. y=f(x) непрерывна на [a,b]. 1) Непрерывная на отрезке достигает (принимает на этом отрезке) своих наибольшего и наименьшего значений. y_min=f(x₁)=m; y_max=f(x₂)=M; x₁,x₂Є[a,b]. Функция может принимать в нескольких точках значения наиб. и наим. 2) Согласно 1) m≤f(x)≤M, т.е. ф-ия ограничена. 3) Если f(a)∙f(b)<0, то сущ. cЄ[a,b ]:f(c)=0. 4)Если f(a)≠f(b) и c – некоторое число между f(a) и f(b), то сущ. cЄ[a,b]:f(c)=C. f(a)=A, f(b)=B. Для определённости A<B; A<C<B; φ(x)=f(x)-C – непрерывна на [a,b] по по теореме об арифмет. дейст. над непрер. ф-иями. φ(a)=f(a)-C=A-C<0; φ(b)=f(b)-C=B-C>0 по 3-ему свойству сущ. cЄ[a,b]: φ(c)=0. φ(a)∙φ(b)<0. f(c)-C=0; f(c)=0. Замечание. Если ф-ия непрерывна на [a,b], то она непрерывна на (a,b) согласно опр. непрерывности на отрезке. Обратное утверждение неверно. Если ф-ия непрерывна на (a,b), то вообще она может иметь разрывы на границы т.А или В и поэтому не являться непрерывной на отрезке.

36. Производной ф-ии y=f(x) в т. x=x₀ называют предел разностного отношения Δy/Δx при Δx→0 и обозначают f’(x₀)=lim Δy/Δx (Δx→0 ) = lim (f(x₀+Δx)-f)x₀))/Δx. Геом. смысл: производная в данной точке чилсенно равна tg угла наклона к касательной к графику ф-ии в данной точке. y=kx+b. y-y₀=k(x-x₀); k=tgα. M₀(x₀;f(x₀)). ℓ:y-f(x₀)=f’(x₀)(x- x₀). Физ. смысл производной:

ΔS=S(t)-S(t₀)=s(t₀+Δt)-S(t₀). υ_ср=ΔS/Δt. υ(t₀)=lim ΔS/Δt (Δt→0)=S’(t₀). При прямолин. движ. производная от пути есть скорость движения.

37. Касательная – предельное положение хорды при M_nM₀ при M_n­→M₀. ℓ:y-f(x₀)=f’(x₀)(x- x₀). Нормаль – прямая, проходящая через данную точку, перпендикулярно к касательной. k₁∙k₂=-1; k₁=f(x₀); k₂=-(1/f(x₀)); y-f(x₀)=-(1/f(x₀))(x- x₀)

38. Ф-ия наз-ся дифференцируемой в т. x₀, если её приращение в этой точке может быть представлено в виде: Δy=A∙Δx+α(Δx)∙Δx, где А – число, независящее от Δх. lim α(Δx) (Δx→0)=0. Теор. Для того, чтобы ф-ия была дифф-ма в данной точке необходимо и достаточно, чтобы она имела конечную производную в данной точке. Док-во. 1) Необходимость. Пусть выполняется Δy=A∙Δx+α(Δx)∙Δx, тогда lim Δy/Δx (Δx→0)=lim (A∙Δx+α(Δx)∙Δx)/Δx=lim (A+α(Δx))=A => f’(x₀)=A. Достаточность: Сущ. предел (1?); f’(x₀)=lim Δy/Δx (Δx→0). f(x)=b+α(x); lim f(x)=b (x→x₀); lim α(x)=0 (x→x₀). Δy/Δx=f’(x₀)+α(Δx); Δy=f’(x0)Δx+α(Δx)Δx. Если f’(x₀)=A, то получаем Δy=A∙Δx+α(Δx)∙Δx. Следствие. Для ф-ии одного дейст. переменного понятие дифф-мость и наличие конеч. производной эквивалент. теореме.

39. Если ф-ия дифф-ма в данной точке, то она непрерывна в этой точке. Док-во:по условию Если f’(x₀)=A, то получаем Δy=A∙Δx+α(Δx)∙Δx, выполняется limΔy=lim (AΔx+α(Δx)Δx) (Δx→0)=A∙0+0∙0=0. Теорема доказана.

40. 1) (с)’=0;

2) (x­^α)’=

3)(a^x)’=a^xlna; (e^x)’=e^x

4)(log_a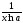x)’=; (lnx)’=1/x

5) (sinx)’=cosx

6)(cosx)’=-sinx

7) (tgx)’=1/cox²x

8)(ctgx)’=-(1/sin²x)

9)(arcsinx)’=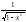

10)(arccosx)’=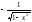

11)(arctgx)’=1/(1+x²)

12)(arcctgx)’=-(1/(1+x²)

13)(shx)’=chx

14)(chx)’=shx

15)(thx)’=1/ch²x

16)(cthx)’=-(1/sh²x)

17)(U(x)±υ(x))’=U’±υ’

18)(U(x)∙υ(x))’=U’υ+Uυ’

19)(U(x)/υ(x))’=(Uυ-Uυ’)/υ²

(sinx)’=lim; (sinx)’=cosx.

41. (U(x)±υ(x))’=U’±υ’; (U(x)∙υ(x))’=U’υ+Uυ’; (U(x)/υ(x))’=(Uυ-Uυ’)/υ²

42. Производная обратной ф-ии: Если ф-ия y=f(x) непрерывна, строго монотонна в некоторой окрестности т. x=x₀, дифф-ма в т. x=x₀, причём f’(x₀)≠0, тогда обратная ф-ия x=[f^-1(y₀)]’=1/f’(x₀). Док-во: В силу условия теоремы, в некоторой окрестност y₀ сущ. обратная строго монотонная непрерывная ф-ия x=f^-1(y); y=y₀. [f^-1(y₀)]’=limΔx/Δy (Δy→0)=lim(f’(y₀+Δx-f^-1(y₀))/Δy. В силу того, что обратная ф-ия и прямая непрерывны , выполняется Δy→0Δx→0; Δy≠0Δx≠0. lim(f’(y₀+Δx-f^-1(y₀))/Δy=lim 1/Δy/Δx=1/f’(x₀). Теорема доказана. Производная сложной функции: Если ф-ия U=φ(x) дифф-ма в т. x=x₀, а ф-ия y=f(U) дифф-ма в т. U=U₀= φ(x₀), то сложная ф-ия y=f[φ(x)]=F(x) дифф-ма в т. x=x₀, причём справедлива формула: (f[φ(x₀)])’=f’(U₀)∙ φ’(x₀). Док-во: (f[φ(x₀)])’=F’(x₀)=lim Δy/Δx (Δx→0). Т.к. ф-ия y=f(U) дифф-ма в т. U=U₀, то приращение можно представить Δy=f’(U₀)ΔU+α(ΔU)ΔU. F’(x₀)=lim (f’(U₀)ΔU+α(ΔU)ΔU)/Δx (Δx→0)=lim f’(U₀)∙(ΔU/Δx)+α(ΔU)∙(ΔU/Δx) = f’(x₀) φ’(x₀). Замечание: может быть получена суперпозицией более чем двух ф-ий. F(t)=f[φ{ψ(t)}]; U= φ(x); x=ψ(t). (φ{ψ(t)}= φ’(x)∙ψ’(t); F’(t)=f’(u)∙φ’(x)∙ψ’(t). Логарифмическая производная: Если ф-ия y=f(x) дифф-ма в т. x=x₀ и в некоторой окрестности т .х f(x)>0, то справедлива формула: f’(x)=f(x)[lnf(x)]’. Док-во. ln f(x) ф-ия определена, т. к. f(x)>0 можно рассматривать как сложную ф-ию. ln y; y=f(x). (ln y)’x=(1/y)∙y’=(1/f(x))∙f’(x). f’(x)=f(x)[lny]’ Теорема доказана.

43. F(x,y)=0 – неявное задание ф-ии. Для того, чтобы найти производную неявно заданной ф-ии уравнение дифф. по x, учитывают, что y зависит от x; затем определяют из полученного уравнения y’. (e^y∙x)_x’+(2x²y)_x’+(1)_x’=(0)_x; e^yy’x+e^y+4xy+2x²y’+0=0;y’(e^yx+2x²)=-e^y-4xy; y’=-(e^y+4xy)/(e^yx+2x²). При дифф. неявно заданной ф-ии производная, значение которых определяется из начального уравнения. Производная ф-ия задана параметрически. x= φ(t), y=ψ(t). t= φ^-1(x); y= ψ[φ^-1(x)]; x’_t= φ(t); y_x’={ψ[φ^-1(x)]}’=ψ’(t)∙[ φ^-1(x)]_x’=ψ’(t)∙(1/ φ’(t)). d_y/d_x=ψ’(t)/ φ’(t).

44. Дифференциалом ф-ии y=f(x) в т.x₀ называют главную часть приращения и обозначают dy=f’(x₀)Δx. Замечание: Если f’(x₀)=0, то определяют дифференциал по формуле dy=f’(x₀)Δx => dy=0. Обозначим Δx=dx, тогда dy=f’(x)dx. Пусть x= φ(t)=> y=f[φ(t)]. dy=(f[φ(t)])’dt; dy=f’(x) φ’(t)dt; dx=φ’(t)dt; dy=f’(x)dx. Вывод. Дифференциал обладает свойство инвариантности формы, справедлива в том случае, когда x-независимая переменная и когда y является функцией.

45. гладкая кривая – если к каждой точке есть касательная, то в каждой точке есть производная. dy=f’(x₀)Δx=tgαΔx. Дифференциал равен приращению касательной в данной точке.

46. Формула для приближённого вычисления ф-ии с помощью дифференциала. Δy≈dy. Δf(x₀+Δx)-f(x₀)≈f’(x₀)Δx; f(x₀+Δx)≈f(x₀)+f’(x₀)Δx+dy.

47. Производная высших порядков функции.y=f(x) дифф-ма на {x}, тогда => f’(x) является ф-ией на {x}. f⁽ⁿ⁾(x)=(f^(n-1)(x))’. Для того чтобы найти n-ную производную, заданной неявной, надо уравнение продифференцировать n раз по х. Функция задана параметрически x= φ(t), y=ψ(t). y’_x=ψ’(t)/ φ’(t). Чтобы определить значение второй производной в данной точке требуется найти значение из исходного уравнения аргумента ф-ии и значение первой производной, полученной после дифференцирования уравнения.

48. Для функции, зависящей от одной переменной   второй и третий дифференциалы выглядят так: