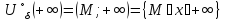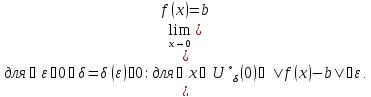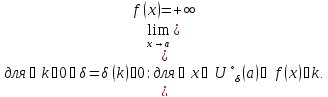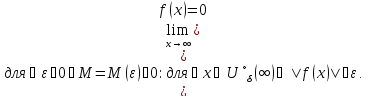matan_rk
.docxОпределения
-
Окрестностью U(x) точки x называют любой интервал, содержащий эту точку.
-
ε-окрестностью точки x (при положительном ε) называют интервал (x−ε, x+ε).
-
Окрестностью точки +∞ называют интервал вида (а, +∞), где а - произвольное действительное число.
-
Окрестностью точки -∞ называют интервал вида (-∞, -а), где а - произвольное действительное число.
-
Окрестностью точки ∞ называют объединение двух бесконечных интервалов вида (-∞, -а) U (а, +∞), где а - произвольное действительное число.
-
Число a называется пределом последовательности {
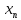 },
если для любого положительного ε
существует номер N=N(ε)
такой, что для всех номеров n≽N
выполняется неравенство |
},
если для любого положительного ε
существует номер N=N(ε)
такой, что для всех номеров n≽N
выполняется неравенство | -a|≺
ε.
-a|≺
ε. -
Если предел числовой последовательности существует и конечен, то он называется сходящейся.
-
Числовая последовательность {
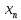 }
называется ограниченной, если она
ограничена и сверху и снизу. (Существуют
M ϵ R и m
ϵ R такие, что для любого
x выполняется неравенство
m≼
}
называется ограниченной, если она
ограничена и сверху и снизу. (Существуют
M ϵ R и m
ϵ R такие, что для любого
x выполняется неравенство
m≼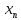 ≼M.
≼M. -
Числовая последовательность {
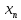 }
называется монотонной, если
}
называется монотонной, если
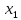 ≽
≽ ≽...≽
≽...≽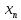 ≽...
или
≽...
или
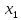 ≼
≼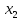 ≼...≼
≼...≼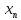 ≼...
≼... -
Числовая последовательность {
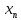 }
называется возрастающей, если
}
называется возрастающей, если
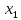 ≺
≺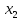 ≺...≺
≺...≺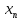 ≺...
≺... -
Числовая последовательность {
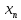 }
называется убывающей, если
}
называется убывающей, если
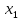 ≻
≻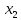 ≻...≻
≻...≻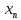 ≻...
≻... -
Числовая последовательность {
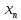 }
называется невозрастающей, если
}
называется невозрастающей, если
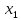 ≽
≽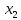 ≽...≽
≽...≽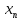 ≽...
≽... -
Числовая последовательность {
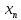 }
называется неубывающей, если
}
называется неубывающей, если
 ≼
≼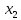 ≼...≼
≼...≼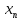 ≼...
≼... -
Последовательность {
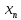 }
называется фундаментальной, если для
любого ε≻0
существует номер N=N(ε)
такой, что при любых m≽N
и n≽N
выполняется неравенство |
}
называется фундаментальной, если для
любого ε≻0
существует номер N=N(ε)
такой, что при любых m≽N
и n≽N
выполняется неравенство |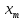 -
-
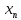 |≺
ε.
|≺
ε. -
Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной.
-
Пусть функция
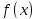 определена в проколотой окрестности
U˚(
определена в проколотой окрестности
U˚(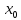 )
точки
)
точки
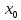 .
Число а называется пределом функции
.
Число а называется пределом функции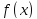 при
при
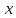 →
→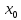 ,
если для любой последовательности {
,
если для любой последовательности {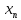 }
точек из U˚(
}
точек из U˚(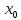 ),
для которой
),
для которой
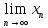 =
=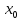 ,
выполняется равенство
,
выполняется равенство
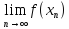 =a.
=a. -
Функция
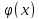 называется бесконечно малой при
называется бесконечно малой при
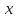 →
→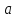 ,
если
,
если
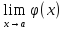 =0.
=0. -
Функция
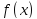 называется бесконечно большой при
называется бесконечно большой при
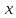 →
→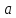 ,
если
,
если
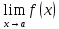 =∞.
=∞. -
Две бесконечно малые при
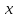 →
→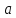 функции
функции
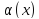 и
и
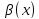 называются бесконечно малыми одного
порядка, если
называются бесконечно малыми одного
порядка, если
 =c,
где с-const, c≠0,
c≠∞.
=c,
где с-const, c≠0,
c≠∞. -
Две бесконечно малые при
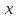 →
→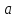 функции
функции
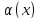 и
и
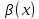 называются несравнимыми, если при
называются несравнимыми, если при
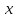 →
→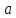 не существует ни конечного, ни бесконечного
предела отношения
не существует ни конечного, ни бесконечного
предела отношения
 .
. -
Две бесконечно малые при
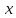 →
→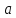 функции
функции
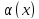 и
и
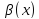 называются эквивалентными бесконечно
малыми, если
называются эквивалентными бесконечно
малыми, если
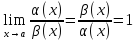 .
. -
Функцию
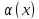 называют бесконечно малой функцией
k-го порядка малости
относительно функции
называют бесконечно малой функцией
k-го порядка малости
относительно функции
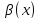 ,
а число k-порядком малости,
если функции
,
а число k-порядком малости,
если функции
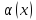 и
и
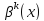 являются бесконечно малыми функциями
при
являются бесконечно малыми функциями
при
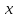 →
→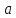 .
. -
Приращением функции называют
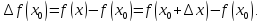
-
Функция
 называется непрерывной в точке
называется непрерывной в точке
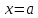 ,
если:
,
если:
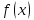 определена в точке
определена в точке
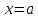 и в U(
и в U(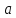 ),
существует
),
существует
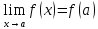 .
. -
Функция
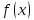 называется
непрерывной на интервале (a,
b), если она непрерывна в
каждой точке этого интервала.
называется
непрерывной на интервале (a,
b), если она непрерывна в
каждой точке этого интервала. -
Функция
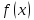 называется
непрерывной на отрезке [a,
b], если она непрерывна в
интервале (a, b)
и непрерывна в точке x=a
справа и в точке x=b
слева.
называется
непрерывной на отрезке [a,
b], если она непрерывна в
интервале (a, b)
и непрерывна в точке x=a
справа и в точке x=b
слева. -
Точка
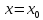 называется точкой разрыва функции
называется точкой разрыва функции
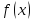 ,
если данная функция не является
непрерывной в точке
,
если данная функция не является
непрерывной в точке
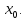
-
Точка
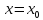 называется точкой устранимого разрыва
функции
называется точкой устранимого разрыва
функции
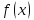 ,
если предел
,
если предел
 существует, но функция не определена
в этой точке или предел не совпадает
со значением функции в данной точке
существует, но функция не определена
в этой точке или предел не совпадает
со значением функции в данной точке
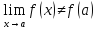 .
. -
Точка
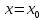 называется точкой разрыва I
рода, если
называется точкой разрыва I
рода, если
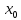 - точка разрыва функции
- точка разрыва функции
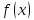 ,
и существуют конечные пределы
,
и существуют конечные пределы
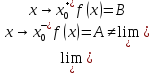 .
. -
Точка
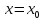 называется точкой разрыва II
рода, если хотя бы один из односторонних
пределов не существует (в частности
равен ∞).
называется точкой разрыва II
рода, если хотя бы один из односторонних
пределов не существует (в частности
равен ∞).
Определение предела по Коши
Основные определения:
|
Тип стремления x |
Окрестности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формулировки теорем
-
Всякая сходящаяся последовательность ограничена.
-
Если существует и конечен
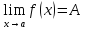 ,
то
,
то
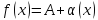 ,
где
,
где
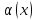 - бесконечно малая при
- бесконечно малая при
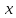 →
→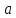 и наоборот.
и наоборот. -
Если
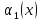 ,
,
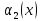 ,...,
,...,
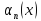 - бесконечно малые при
- бесконечно малые при
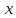 →
→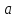 функции, то
функции, то
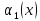 +
+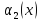 +...+
+...+
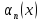 - бесконечно малая при
- бесконечно малая при
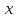 →
→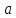 .
. -
Если
 - бесконечно малая при
- бесконечно малая при
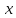 →
→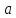 функция,
функция,
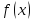 - ограниченная функция, то
- ограниченная функция, то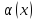 *
*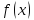 - бесконечно малая при
- бесконечно малая при
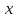 →
→ .
. -
Если
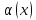 - бесконечно малая при
- бесконечно малая при
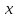 →
→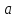 функция,
функция,
 ,
то
,
то
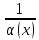 - бесконечно большая при
- бесконечно большая при
 →
→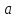 .
.
Если
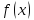 - бесконечно большая при
- бесконечно большая при
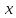 →
→ функция,
функция,
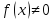 ,
то
,
то
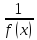 - бесконечно малая при
- бесконечно малая при
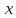 →
→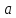 .
.
-
Бесконечно малые при
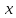 →
→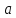 функции
функции
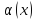 и
и
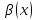 эквивалентны тогда и только тогда,
когда их разность имеет более высокий
порядок малости при
эквивалентны тогда и только тогда,
когда их разность имеет более высокий
порядок малости при
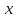 →
→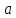 по сравнению с каждой из них.
по сравнению с каждой из них. -
Сумма бесконечно малых при
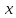 →
→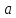 функций различных порядков эквивалентна
бесконечно малой низшего порядка.
функций различных порядков эквивалентна
бесконечно малой низшего порядка.

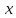 →
→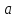
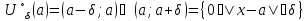
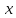 →
→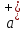
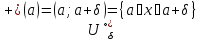
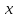 →
→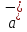
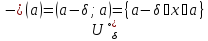
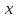 →∞
→∞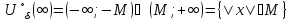
 →-∞
→-∞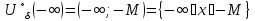
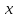 →+∞
→+∞