Matanaliz

Отсюда можно вывести общий вид дифференциала n-го порядка от функции  :

49. Теорема Ферма. Если ф-ия y=f(x) непрерывна на [a,b], принимает внутри сегмента в т. x=cЄ(a,b) своё наиб. или наим. значение, причём в т. х=с ф-ия дифф-ма, тогда f’(c)=0. Док-во: f(c) – наиб. значение ф-ии на [a,b] f(x)≤f(c). f’(c)=lim Δy/Δx= lim(f(c+Δx)-f(c))/Δx (Δx→0). Δy= f(c+Δx)-f(c)≤0; Δx>0; Δy/Δx≤0; lim Δy/Δx≤0 (Δx→0); f’(c)≤0; Δx<0; f’(c)≥0. Т.к. ф-ия дифф-ма в c, то f’(c) существует конечно число: f’(c)≤0; f’(c)≥0 => f’(c)=0. Теорема Ролля: Если ф-ия y=f(x) непрерывна на [a,b], и дифф-ма на (a,b), кроме того f(a)=f(b), тогда существует т. x=cЄ(a,b):f’(c)=0.

1) Если ф-ия постоянна : y=c=f(a)=f(b)=const; y’=0 при любом cЄ(a,b). 2)Если y=f(x)≠const. Т.к. ф-ия непрерывна, то одно из своих двух наиб. или наим. значений принимает внутри сегмента. В этой точке для ф-ии выполняются все условия т. Ферма, следовательно производная в этой точке будет равна 0. Теорема Лагранжа: Если ф-ия y=f(x) непрерывна на [a,b], дифф-ма на (a,b), то существует т. cЄ(a,b): f(b)-f(a)=f’(c)(b-a). Док-во: φ(x)=f(x)+λx; λ=(f(b)-f(a))/(b-a). φ(x) удовлетворяет всем условия т. Ролля, является непрерывной как сумма двух непрерывных ф-ий, дифф-ма на (a,b), потому что φ’(x)=f’(x)-λ. φ(a)=f(a)-λa=; φ(b)=f(b)-λb=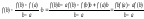=> φ(a)= φ(b). Для φ(x) выполняются все условия т. Ролля. Тогда сущ. cЄ(a,b): φ’(c)=0. f’(c)=λ=>f’(c)=(f(b)-f(a))/(b-a). Теорема Коши: Если f(x) и φ(x) непрерывны на [a,b], дифф-мы на (a,b), φ’(x)≠0 и (a,b), тогда сущ. т. сЄ(a,b): 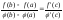Док-во: ψ(x)=f(x)-λ φ(x); ψ’(x)=f’(x)-λ φ’(x); λ=(f(b)-f(a))/( φ(b)- φ(a)). ψ(a)=ψ(b). Сущ. c=>ψ’(c)=0; f’(c)-λ φ’(c)=0; λ=f’(c)/ φ’(c); ψ’(c)=0. Т. Лопиталя-Бернулли. Если f(x) и φ(x) являются бесконеч. малыми и бесконч. большими ф-ями при х→а, тогда lim f(x)/ φ(x)=lim f’(x)/ φ’(x) (х→а), при условии, что сущ. предел правой части равенства, т.е. lim f’(x)/ φ’(x). Докажем теорему случаем, когда f(a)= φ(a)=0; φ’(a)≠0; lim f(x)/φ(x)=lim (f(x)-f(a))/(φ(x)-φ(a))=(0/0)=lim (f(x)-f(a)/(x-a))/(φ(x)-φ(a))/(x-a))=lim f’(x)/φ’(x) (x→a)

50. 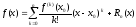формула Тейлора. 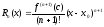Получение остатка в форме Лагранжа.

51. формула Маклорена. Вычисление числа е с точность 0,001: x=1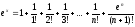 ; e^c/(n+1)!<3¹/(n+1)!<ξ; cЄ(0,1); n-?; 3/5040<0,001; 3/7!<0,001; n+1=7; n=6; e≈1+1+0.5+1/6+1/24+1/120/+1/720=2,5+0,1667+0,0417+0.0089+0.0014=2.718

52. Необходимое условие монотонности: Если на некотором интервале ф-ия возрастает и является дифф-мой, то её производная на этом интервале не отрицательна y’≥0; если убывает, то производная не положительна y’≤0. Док-во: y=f(x) – возрастает на (a,b); x₀Є(a,b); f’(x₀)= 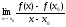; x>x₀=>f(x)>f(x₀); Δy>0; Δx>0 => Δy/Δz>0. x<x₀=>f(x)<f(x₀); x-x₀=Δx<0; f(x)-f(x₀)=Δy<0; Δy/Δx>0. Если ф-ия возрастает, то приращение ф-ии и аргумента одного знака. f’(x₀)=lim Δy/Δx≥0 (Δx→0); f’(x₀)≥0. Если ф-ия убывает, то приращение аргумента и ф-ии имеют разные знаки. Δy/Δx<0=>f’(x₀)≤0. Теорема доказана. Достаточное условие монотонности: Если на некотором интервале y’>0, то ф-ия возрастает, если y’<0, то ф-ия убывает, если y’=0, то ф-ия является постоянной. Док-во: (a,b)-ф-ия дифф-ма. x₁, x₂Є(a,b): x₁<x₂. На сегменте x₁, x₂ выполняются все условия теоремы Лагранжа. f(x₂)-f(x₁)=f’(c)(x₂-x₁); y’>0=>f’(c)>0. Правая часть положительна f’(x₂)>f(x₁). y’<0=>f’(c)<0; x₂-x₁>0; f(x₂)-f(x₁)<0; f(x₂)<f(x₁)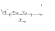

53. Первое достаточное условие экстремума: Если в некоторой окрестности x=x₀ ф-ия y=f(x) дифф-ма, f’(x₀)=0, а при переходе через x₀ f’(x) меняет знак, то x=x₀ – точка экстремума, причём, если знак меняется с + на -, то x₀ точка максимума, если с – на +, то х₀ точка минимума. Док-во: Пусть знак производной меняется с + на -. Пусть х=х₁ из окрестности х₀, тогда между х₁ и х₀ выполняются все условия теоремы Лагранжа, тогда х₁>x₀; [x₀, x₁]. f(x₁)-f(x₀)=f’(ψ)(x₁-x₀). Сущ. ψЄ(х₀, х₁), f’(ψ)<0; x₁-x₀>0;

f(x₁)-f(x₀)<0; f(x₁)<f(x₀)>0. x₂<x₀; [x₂,x₀]=> f(x₀)-f(x₂)=f’(c)(x₀-x₂); f’(x)>0; x₀-x₂>0; f(x₀)-f(x₂)>0. Таким образом значение ф-ии слева от x₀ и справа от х₀ меньше, чем значение f(x₀), т.е. f(x₀) в данной окрестности будет наиб, а х₀ точка локального максимума. Если знак производной меняется с минума на плюс – док-ся аналогично. Второе достаточное условие экстремума: Если ф-ия y=f(x) двжды дифф-ма в некоторой окрестности х=х₀ f’(x₀)=0; f’’(x₀)≠0, то x₀ то чка экстремума, причём если f’’(x₀)>0, то х₀ точка минимума, f’’(x₀)<0 – точка маскимума. Док-во: Пусть f’(x₀)=0, f’’(x₀)>0. f’(x) в точке х₀ – возрастает, но если она возрастает, проходя через 0,f’(x) меняет знак с – на +. По первому достаточному признаку экстремума х₀ точка минимума. f’(x₀)=0, f’’(x₀)<0; f’(x) меняет знак с + на -, х₀-точка максимума. Теорема доказана.

54. Выпуклый. график лежит под любой касательной. Вогнутый. График выше любой своей касательной. Понятие выпуклости, вогнутости применяется к дифф-м ф-ям, притом как минимум дважды дифф-мы. tgα₁<tgα₂; k₁<k₂; f’(x₁)<f’(x₂). f’(x) возрастает. (Из необходимого условия монотонности). Достаточное условие выпуклости, вогнутости: Если f’’(x)>0 на (a,b), то на этом графике ф-ия вогнутая, если f’’(x)<0 – выпуклая. Если в т. х₀ ф-ия дважды дифф-ма, в этой точке график ф-ии имеет касательную и при переходе через эту точку график меняет выпуклость на вогнутость. или вогнутость на выпуклость, то т. графика (x₀, y₀) – точка перегиба графика. достаточное условие точки перегиба: Если f’’(x₀)=0 и f’’(x) меняет знак при переходе через х₀, то х₀ – точка перегиба. Если f’’(x) не меняет знак при переходе через х₀, то это не является точкой перегиба.

55. Асимптотой графика называют прямую такую, что точка графика при удалении её от начала координат сколь угодно близко подходит к асимптоте, т.е. расстояние между точкой графика и асимптотой стремиться к 0. x=a вертикальная асимптота в точке разрыва второго рода. y=kx+b наклонные и горизонтальные асимптоты при x→∞.