40, 25, 30, 50, 35, 20, 50, 32, 15, 40, 20, 40, 45, 30, 50, 25, 35, 20, 35, 40.

Первым делом названные величины надо упорядочить в порядке возрастания. Результаты представлены в табл.1. В первом столбце – номера различных численных значений (в порядке возрастания), названных потребителями. Во втором столбце приведены сами значения цены, названные ими. В третьем столбце указано, сколько раз названо то или иное значение.

Таблица 1

Эмпирическая оценка функции спроса и ее использование

№ п/п (i)	Цена pi	Повто-ры Ni	Спрос D(pi)	Прибыль (p-10)D(р)	Прибыль (p-15)D(р)	Прибыль (p-25)D(р)
1	15	1	20	100	0	-
2	20	3	19	190	95	-
3	25	2	16	240	160	0
4	30	2	14	280	210	70
5	32	1	12	264	204	84
6	35	3	11	275	220	110
7	40	4	8	240	200	120
8	45	1	4	140	120	80
9	50	3	3	120	105	75

Таким образом, 20 потребителей назвали 9 конкретных значений цены (максимально допустимых или приемлемых для них значений), каждое из значений, как видно из третьего столбца, названо от 1 до 4 раз. Теперь легко построить выборочную функцию спроса в зависимости от цены. Она будет представлена в четвертом столбце, который заполним снизу вверх. Спрос как функция от цены р обозначен D(p) (от англ. Demand – спрос). Если мы будем предлагать товар по цене свыше 50 руб., то его не купит никто из опрошенных. При цене 50 руб. появляются 3 покупателя. Записываем 3 в четвертый столбец в девятую строку. А если цену понизить до 45? Тогда товар купят четверо – тот единственный, для кого максимально возможная цена – 45, и те трое, кто был согласен на более высокую цену – 50 руб. Таким образом, легко заполнить столбец 4, действуя по правилу: значение в клетке четвертого столбца равно сумме значений в находящейся слева клетке третьего столбца и в лежащей снизу клетке четвертого столбца. Например, за 30 руб. купят товар 14 человек, а за 20 руб. – 19.

Зависимость спроса от цены – это зависимость четвертого столбца от второго. Табл.1 дает нам девять точек такой зависимости. Зависимость можно представить на рисунке, в координатах «спрос – цена» (рис. 1). Если абсцисса – это спрос, а ордината – цена, то девять точек на кривой спроса, перечисленные в порядке возрастания абсциссы, имеют вид:

(3; 50), (4; 45), (8; 40), (11; 35), (12; 32), (14; 30),

(16; 25), (19; 20), (20; 15).

Эти девять точек можно использовать для построения кривой спроса каким-либо графическим или расчетным способом, например, методом наименьших квадратов (см.9.2).

Рис. 1. Кривая спроса

Кривая спроса, в соответствии с экономической теорией, убывает, имея направления от левого верхнего угла чертежа к правому. Однако заметны отклонения от гладкого вида функции, связанные, в частности, с естественным пристрастием потребителей к круглым числам. Заметьте, все опрошенные, кроме одного, назвали числа, кратные 5 руб.

Данные табл.1 могут быть использованы для выбора цены продавцом-монополистом, или организацией, действующей на рынке монополистической конкуренции. Пусть расходы на изготовление или оптовую покупку единицы товара равны 10 руб. Например, оптовая цена книги – 10 руб. По какой цене ее продавать на том рынке, функцию спроса для которого мы только что нашли? Для ответа на этот вопрос вычислим суммарную ожидаемую прибыль, т.е. произведение прибыли на одном экземпляре (p-10) на число проданных (точнее, запрошенных) экземпляров D(p). Результаты приведены в пятом столбце табл.1. Максимальная прибыль, равная 280 руб., достигается при цене 30 руб. за экземпляр. При этом из 20 потенциальных покупателей окажутся в состоянии заплатить за книгу 14, т.е. 70% .

Если же удельные издержки производства, приходящиеся на одну книгу (или оптовая цена), повысятся до 15 руб., то данные столбца 6 табл.1 показывают, что максимальная прибыль, равная 220 руб. (она, разумеется, меньше, чем в предыдущем случае), достигается при более высокой цене – 35 руб. Эта цена доступна 11 потенциальным покупателям, т.е. 55% от всех возможных покупателей. При дальнейшем повышении издержек, скажем, до 25 руб., как вытекает из данных седьмого столбца табл.1, максимальная прибыль, равная 120 руб., достигается при цене 40 руб. за единицу товара, что доступно 8 лицам, т.е. 40% покупателей. Отметьте, что при повышении оптовой цены на 10 руб. оказалось выгодным увеличить розничную лишь на 5, поскольку более резкое повышение привело бы к такому сокращению спроса, которое перекрыло бы эффект от повышения удельной прибыли (т.е. прибыли, приходящейся на одну проданную книгу).

Представляет интерес анализ оптимального объема выпуска при различных значениях удельных издержек (табл.2).

В табл.2 звездочками указаны максимальные значения прибыли при том или ином значении издержек, не включенном в табл.1. Для удобства результаты расчетов оптимальных объемов выпуска и соответствующих цен из табл.1 и 2 приведены в табл.3.

Таблица 2

Прибыль при различных значениях издержек

№ (i)	Цена pi	Спрос D(pi)	Прибыль (p-5)D(р)	Прибыль (p-20)D(р)	Прибыль (p-30)D(р)	Прибыль (p-35)D(р)	Прибыль (p-40)D(р)
1	15	20	200	-	-	-	-
2	20	19	285	0	-	-	-
3	25	16	320	80	-	-	-
4	30	14	350 *	140	0	-	-
5	32	12	324	144	24	-	-
6	35	11	330	165 *	55	0	-
7	40	8	280	160	80 *	40	0
8	45	4	160	100	60	40	20
9	50	3	135	90	60	45 *	30 *

Таблица 3

Зависимость оптимального выпуска и цены от издержек

Издержки	5	10	15	20	25	30	35	40
Оптимальный выпуск	14	14	11	11	8	8	3	3
Цена	30	30	35	35	40	40	50	50

Как видно из табл.3, с ростом издержек оптимальный выпуск падает, а цена растет. При этом изменение издержек на 5 единиц может вызывать, а может и не вызывать повышения цены. В этом проявляется микроструктура функции спроса – небольшое повышение цены может привести к тому, что значительные группы покупателей откажутся от покупок, и прибыль упадет.

Этот эффект напоминает известное в экономической теории разделение налогового бремени между производителем и потребителем. Неверно говорить, что производитель перекладывает издержки или, конкретно, налоги, на потребителя, повышая цену на их величину, поскольку при этом сокращается спрос (и выпуск), а потому и прибыль производителя.

Дальнейшее ясно – если оптовая цена будет повышаться, то и дающая максимальную прибыль розничная цена также будет повышаться, и все меньшая доля покупателей сможет приобрести товар. Крайняя точка – оптовая цена, равная 45 руб. Тогда только трое (15 %) купят товар за 50 руб., а прибыль продавца составит только 15 руб. Наглядно видно, что повышение издержек производства приводит к ориентации производителя на наиболее богатые слои населения, но и повышение цен (до оптимального для монополиста-производителя уровня) не приводит к повышению прибыли, напротив, она снижается, и при этом большинство потенциальных потребителей не в состоянии купить товар. Таково влияние инфляции издержек на экономическую жизнь.

Отметим, что рыночные структуры не в состоянии обеспечить всех желающих – это просто не выгодно. Так, из 20 опрошенных лишь 14, т.е. 70%, могут рассчитывать на покупку, даже при минимальных издержках и ценах. Если общество желает чем-либо обеспечить всех граждан, оно должно раздавать это благо бесплатно, как это делается, например, с учебниками в школах.

Описанный выше метод оценивания спроса был разработан в Институте высоких статистических технологий и эконометрики в 1993 г.

Для изучения предпочтений потребителей часто используют более изощренные методы. Рассмотрим некоторые из них.

46)Биномиальная и гипергеометрическая модели выборки, их близость в случае большого объема генеральной совокупности по сравнению с выборкой.

Биномиальная модель выборки. Она применяется для описания ответов на закрытые вопросы, имеющие две подсказки, например, «да» и «нет».

Пусть объем выборки равен n. Тогда ответы опрашиваемых можно представить как X₁ , X₂ ,…,X_n , где X_i = 1, если i-й респондент выбрал первую подсказку, и X_i = 0, если i-й респондент выбрал вторую подсказку, i=1,2,…,n. В вероятностной модели предполагается, что случайные величины X₁ , X₂ ,…,X_n независимы и одинаково распределены. Поскольку эти случайные величины принимают два значения, то ситуация описывается одним параметром р – долей выбирающих первую подсказку во всей генеральной совокупности. Тогда

Р(X_i = 1) = р, Р(X_i = 0)= 1–р, i=1,2,…,n.

Пусть m = X₁ + X₂ +…+X_n . Оценкой вероятности р является частота р*=m/n. При этом математическое ожидание М(р*) и дисперсия D(p*) имеют вид

М(р*) = р, D(p*)= p(1–p)/n.

По закону больших чисел (ЗБЧ) теории вероятностей (в данном случае – по теореме Бернулли) частота р* сходится (т.е. безгранично приближается) к вероятности р при росте объема выборки. Это и означает, что оценивание проводится тем точнее, чем больше объем выборки

С помощью теоремы Муавра-Лапласа могут быть построены доверительные интервалы для неизвестной эконометрику вероятности. Сначала заметим, что из этой теоремы непосредственно следует, что

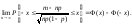
Поскольку функция стандартного нормального распределения симметрична относительно 0, т.е. 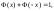то

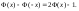
Зададим доверительную вероятность . Пусть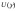удовлетворяет условию

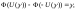т.е.

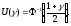
Из последнего предельного соотношения следует, что

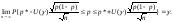
К сожалению, это соотношение нельзя непосредственно использовать для доверительного оценивания, поскольку верхняя и нижняя границы зависят от неизвестной вероятности. Однако с помощью метода наследования сходимости (см. гл.4 или [3, п.2.4]) можно доказать, что

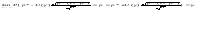
Следовательно, нижняя доверительная граница имеет вид

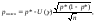
в то время как верхняя доверительная граница такова:

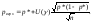
Наиболее распространенным (в прикладных исследованиях) значением доверительной вероятности является 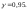Иногда употребляют термин «95% доверительный интервал». Тогда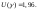

47)Интегральное оценивание выборочной доли.

48)Метод проверки гипотезы о равенстве долей

49)Среднее арифметическое и его св-ва. Сумма всех отклонений индивидуальных значений от выборочной средней арифметической. Изменение среднего арифметического при изменении всех значений варьирующего признака на одну и ту же величину.

Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:

Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.

2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:

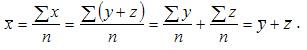
3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:

4.Сумма квадратов отклонений вариантов от средней меньше, чем сумма квадратов отклонений от любой другой произвольной величины а, т.е:

5. Если все варианты ряда уменьшить или увеличить на одно и то же число , то средняя уменьшится на это же число а:

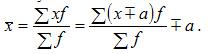
6.Если все варианты ряда уменьшить или увеличить в А раз, то средняя также уменьшится или увеличится в А раз:

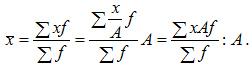
7.Если все частоты (веса) увеличить или уменьшить в d раз, то средняя арифметическая не изменится:

51, 52) Ср. геометрическое и его св-ва. Среднее квадратическое и ср. гармоническое.

Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:

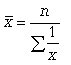
В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид

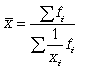
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для простой средней геометрической

Для взвешенной средней геометрической

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула простой средней квадратической

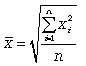
Формула взвешенной средней квадратической

В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:

а) установление обобщающего показателя совокупности;

б) определение для данного обобщающего показателя математического соотношения величин;

в) замена индивидуальных значений средними величинами;

г) расчет средней с помощью соответствующего уравнения.

54)Среднее по Коши и его частные случаи. Члены вариационного ряда как средние по Коши.

А как вычислять средние? Известны различные виды средних величин: среднее арифметическое, медиана, мода, среднее геометрическое, среднее гармоническое, среднее квадратическое. Напомним, что общее понятие средней величины введено французским математиком первой половины ХIХ в. академиком О. Коши. Оно таково: средней величиной является любая функция f(X₁, X₂,...,X_n) такая, что при всех возможных значениях аргументов значение этой функции не меньше, чем минимальное из чисел X₁, X₂,...,X_n, и не больше, чем максимальное из этих чисел. Все перечисленные выше виды средних являются средними по Коши.

При допустимом преобразовании шкалы значение средней величины, очевидно, меняется. Но выводы о том, для какой совокупности среднее больше, а для какой – меньше, не должны меняться (в соответствии с требованием инвариантности выводов, принятом как основное требование в теории измерений). Сформулируем соответствующую математическую задачу поиска вида средних величин, результат сравнения которых устойчив относительно допустимых преобразований шкалы.

Пусть f(X₁, X₂,...,X_n) – среднее по Коши. Пусть среднее по первой совокупности меньше среднего по второй совокупности:

f(Y₁, Y₂,...,Y_n) < f(Z₁, Z₂,...,Z_n).

Тогда согласно теории измерений для устойчивости результата сравнения средних необходимо, чтобы для любого допустимого преобразования g из группы допустимых преобразований в соответствующей шкале было справедливо также неравенство

f(g(Y₁), g(Y₂),...,g(Y_n)) < f(g(Z₁), g(Z₂),...,g(Z_n)),

т.е. среднее преобразованных значений из первой совокупности также было меньше среднего преобразованных значений для второй совокупности. Причем сформулированное условие должно быть верно для любых двух совокупностей Y₁, Y₂,...,Y_n и Z₁, Z₂,...,Z_n. И, напомним, для любого допустимого преобразования. Средние величины, удовлетворяющие сформулированному условию, назовем допустимыми (в соответствующей шкале). Согласно теории измерений только такими средними можно пользоваться при анализе мнений экспертов и иных данных, измеренных в рассматриваемой шкале.

С помощью математической теории, развитой в монографии [12], удается описать вид допустимых средних в основных шкалах. Сразу ясно, что для данных, измеренных в шкале наименований, в качестве среднего годится только мода.

Средние величины в порядковой шкале. Рассмотрим обработку, для определенности, мнений экспертов, измеренных в порядковой шкале. Справедливо следующее утверждение.

Теорема 1. Из всех средних по Коши допустимыми средними в порядковой шкале являются только члены вариационного ряда (порядковые статистики).

Теорема 1 справедлива при условии, что среднее f(X₁, X₂,...,X_n) является непрерывной (по совокупности переменных) и симметрической функцией. Последнее означает, что при перестановке аргументов значение функции f(X₁, X₂,...,X_n) не меняется. Это условие является вполне естественным, ибо среднюю величину мы находим для совокупности (множества), а не для последовательности. Множество не меняется в зависимости от того, в какой последовательности мы перечисляем его элементы.

Согласно теореме 1 в качестве среднего для данных, измеренных в порядковой шкале, можно использовать, в частности, медиану (при нечетном объеме выборки). При четном же объеме следует применять один из двух центральных членов вариационного ряда – как их иногда называют, левую медиану или правую медиану. Моду тоже можно использовать – она всегда является членом вариационного ряда. Но никогда нельзя рассчитывать среднее арифметическое, среднее геометрическое и т.д.

56,57)Среднее по Колмогорову – определение и частные случаи. Степенные средние и среднее геометрическое как частные случаи средних по Колмогорову.

Средние по Колмогорову. Естественная система аксиом (требований к средним величинам) приводит к так называемым ассоциативным средним. Их общий вид нашел в 1930 г. А.Н.Колмогоров [9]. Теперь их называют «средними по Колмогорову». Они являются обобщением нескольких из перечисленных выше средних.

Для чисел X₁, X₂,...,X_n среднее по Колмогорову вычисляется по формуле

G{(F(X₁) + F(X₂)+... + F(X_n))/n},

где F – строго монотонная функция (т.е. строго возрастающая или строго убывающая), G – функция, обратная к F. Среди средних по Колмогорову – много хорошо известных персонажей. Так, если F(x) = x, то среднее по Колмогорову – это среднее арифметическое, если F(x) = ln x – среднее геометрическое, если F(x) = 1/x – среднее гармоническое, если F(x) = x² – среднее квадратическое, и т.д. (в последних трех случаях усредняются положительные величины). Среднее по Колмогорову – частный случай среднего по Коши. С другой стороны, такие популярные средние, как медиана и мода, нельзя представить в виде средних по Колмогорову. В монографии [12] доказаны следующие утверждения.

Теорема 3. При справедливости некоторых внутриматематических условий регулярности в шкале интервалов из всех средних по Колмогорову допустимым является только среднее арифметическое.

Таким образом, среднее геометрическое или среднее квадратическое температур (в шкале Цельсия), потенциальных энергий или координат точек не имеют смысла. В качестве среднего надо применять среднее арифметическое. А также можно использовать медиану или моду.

Теорема 4. При справедливости некоторых внутриматематических условий регулярности в шкале отношений из всех средних по Колмогорову допустимыми являются только степенные средние с F(x) = x^с , и среднее геометрическое.

Замечание. Среднее геометрическое является пределом степенных средних при

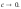
58)ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ

распределениевыборки, -распределение вероятностей, к-рое определяется по выборке для оценивания истинного распределения. Пусть результаты наблюдений Х₁, . . ., Х _п - взаимно независимые и одинаково распределенные случайные величины с функцией распределения и пустьX₍₁₎< X₍₂₎< . . . <X_(n)- соответствующий вариационный ряд. Эмпирическим распределением, соответствующим Х₁, . . ., Х _п, наз. дискретное распределение, приписывающее каждому значению Х _k вероятность 1/n. Функция Э. р. наз. эмпирической функцией; распределения, является ступенчатой функцией со скачками, кратными 1/п, в точках, определяемых величинамиХ (1), . . ., Х _(п): 


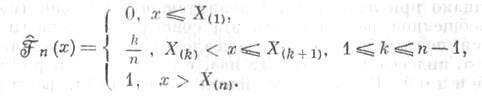
При фиксированных значениях Х ₁, . . ., Х _п функция обладает всеми свойствами обычной функции распределения. При каждом фиксированном действительном хфункцияявляется случайной величиной как функция Х₁, . . ., Х _п. Таким образом, Э. р., соответствующее выборке Х ₁, . . ., Х _п, задается семейством случайных величин зависящих от действительного параметрах. При этом для фиксированного x

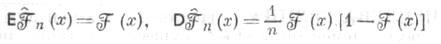и 


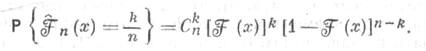
В соответствии с законом больших чисел при каждомх. Ото означает, что - несмещенная исостоятельная оценкафункции распределенияФункция Э. р. равномерно по хсходится с вероятностью 1 кприили, если
 
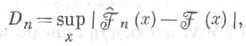то 
 
(теоремаГливенко - Кантелли).
Величина D_n служит мерой близости кА. Н. Колмогоров (1933) нашел предельное распределение:
для непрерывной функции 


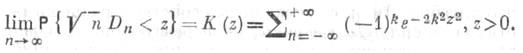
Если неизвестна, то для проверки гипотезы о том, что эта функция есть заданнаянепрерывная функцияприменяются критерии, основанные на статистиках типаD_n (см. Колмогорова критерий, Колмогорова- Смирнова критерий, Непараметрические методы статистики). 
Моменты и любые другие характеристики Э. р. наз. выборочными (эмпирическими) моментами и характеристиками, напр.:

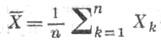- выборочное среднее,

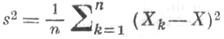- выборочная дисперсия,

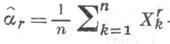- выборочный момент r- го порядка. 
Выборочные характеристики служат статистич. оценками соответствующих характеристик исходного распределения.

59)Основные понятия теории измерений. Определения, примеры, группы допустимых преобразований для шкал наименований, порядка, интервалов, отношений, разностей, абсолютной. Требование устойчивости статистических выводов относительно допустимых преобразований шкал.

Измерение — установление соответствия между множествами объектов и множеством "стандартных моделей объектов", которые и составляют измерительную шкалу. Термины “измерение” и “шкалирование” употребляются как синонимы. Измерения и шкалы являются инструментами формализации и обобщения эмпирических наблюдений. 
         Свойства шкал определяются отношениями, заданными на множестве стандартных моделей шкалируемых объектов. Определенным типам шкал (шкала наименований, шкала порядка, шкала интервалов, шкала отношений)  соответствуют различные правила, ограничивающие возможные операции со стандартными моделями объектов, способы обработки результатов измерения и их интерпретации. Формальное обоснование и анализ свойств шкал различных типов приведены в работе [13].

        Важно, что в ряду шкал - наименований, порядка, интервалов, отношений - увеличивается мощность шкал: качественные измерения сменяются количественными, возрастают возможности оценки свойств объектов, различий и отношений их свойств, применения арифметических операций, статистических мер и критериев, расширяются пределы инвариантности измерений. Более мощные шкалы обладают всеми возможностями шкал менее мощных, что связывает все шкалы в единую систему измерений.

Шкала наименований

Шкала наименований получается путем присвоения “имен” объектам. При этом нужно разделить множество объектов на непересекающиеся подмножества.

Иными словами, объекты сравниваются друг с другом и определяется их эквивалентность–неэквивалентность. В результате данной процедуры образуется совокупность классов эквивалентности. Объекты, принадлежащие к одному классу, эквивалентны друг другу и отличны от объектов, относящихся к другим классам. Эквивалентным объектам присваиваются одинаковые имена.

Операция сравнения является первичной для построения любой шкалы. Для построения такой шкалы нужно, чтобы объект был равен или подобен сам себе (х = х для всех значений х), т. е. на множестве объектов должно быть реализовано отношение рефлексивности. Для психологических объектов, например испытуемых или психических образов, это отношение реализуемо, если абстрагироваться от времени. Но поскольку операции попарного (в частности) сравнения множества всех объектов эмпирически реализуются неодновременно, то в ходе эмпирического измерения даже это простейшее условие не выполняется.

Следует запомнить: любая шкала есть идеализация, модель реальности, даже такая простейшая, как шкала наименований.

На объектах должно быть реализовано отношение симметрии R (X =Y) ®R (Y =X) и транзитивности R (X =Y, Y = Z) ®R (X = Z). Но на множестве результатов психологических экспериментов эти условия могут нарушаться.

Кроме того, многократное повторение эксперимента (накопление статистики) приводит к “перемешиванию” состава классов: в лучшем случае мы можем получить оценку, указывающую на вероятность принадлежности объекта к классу.

Таким образом, нет оснований говорить о шкале наименований (номинативной шкале, или шкале строгой классификации) как о простейшей шкале, начальном уровне измерения в психологии.

Существуют более “примитивные” (с эмпирической, но не с математической точки зрения) виды шкал: шкалы, основанные на отношениях толерантности; шкалы “размытой” классификации и т. п.

О шкале наименований можно говорить в том случае, когда эмпирические объекты просто “помечаются” числом. Примером таких пометок являются номера на майках футболистов: цифру “1” по традиции получает вратарь, и это указывает на то,что по своей функции он отличен от всех остальных игроков; но его функция на футбольном поле эквивалентна функции других вратарей, если не учитывать качество игры.

В принципе, вместо чисел при использовании шкалы наименований необходимо применять другие символы, ибо числовая шкала (натуральный ряд чисел) характеризуется разными системами операций.

Итак, если объекты в каком-то отношении эквивалентны, то мы имеем право отнести их к одному классу. Главное, как говорил Стивене, не приписывать один и тот же символ разным классам или разные символы одному и тому же классу.

Для этой шкалы допустимо любое взаимно однозначное преобразование.

Несмотря на тенденцию “завышать” мощность шкалы, психологи очень часто применяют шкалу наименований в исследованиях. “Объективные” измерительные процедуры при диагностике личности приводят к типологизации: отнесению конкретной личности к тому или иному типа. Примером такой типологии являются классические темпераменты: холерик, сангвиник, меланхолик и флегматик.

В “субъективной” психологии измерения используются также классификации. Примеры: сортировка объектов по Гарднеру, метод константных стимулов в психофизике и т. д.

Исследователь, пользующийся шкалой наименований, может применять следующие инвариантные статистики: относительные частоты, моду, корреляции случайных событий, критерий c².

Порядковая шкала (или ранговая)

Строится на отношении тождества и порядка. Субъекты в данной шкале ранжированы. Но не все объекты можно подчинить отношению порядка. Например, нельзя сказать, что больше круг или треугольник, но можно выделить в этих объектах общее свойство-площадь, и таким образом становится легче установить порядковые отношения. Для данной шкалы допустимо монотонное преобразование. Такая шкала груба, потому что не учитывает разность между субъектами шкалы. Пример такой шкалы: балльные оценки успеваемости (неудовлетворительно, удовлетворительно, хорошо, отлично), шкала Мооса.

Интервальная шкала (она же Шкала разностей)

Здесь происходит сравнение с эталоном. Построение такой шкалы позволяет большую часть свойств существующих числовых систем приписывать числам, полученным на основе субъективных оценок. Например, построение шкалы интервалов для реакций. Для данной шкалы допустимым является линейное преобразование. Это позволяет приводить результаты тестирования к общим шкалам и осуществлять, таким образом сравнение показателей. Пример: шкала Цельсия.

Начало отсчёта произвольно, единица измерения задана. Допустимые преобразования — сдвиги. Пример: измерение времени.

Абсолютная шкала (она же Шкала отношений)

это интервальная шкала, в которой присутствует дополнительное свойство — естественное и однозначное присутствие нулевой точки. Пример: число людей в аудитории. В шкале отношений действует отношение "во столько-то раз больше". Это единственная из четырёх шкал имеющая абсолютный ноль. Нулевая точка характеризует отсутствие измеряемого качества. Данная шкала допускает преобразование подобия (умножение на константу). Определение нулевой точки — сложная задача для психологических исследований, накладывающая ограничение на использование данной шкалы. С помощью таких шкал могут быть измерены масса, длина, сила, стоимость (цена). Пример: шкала Кельвина (температур, отсчитанных от абсолютного нуля, с выбранной по соглашению специалистов единицей измерения — Кельвин).

Из рассмотренных шкал первые две являются неметрическими, а остальные -метрическими.

С вопросом о типе шкалы непосредственно связана проблема адекватности методов математической обработки результатов измерения. В общем случае адекватными являются те статистики, которые инвариантны относительно допустимых преобразований используемой шкалы измерений.

Шкала отношений.

        Шкала отношений отличается от интервальной шкалы введением “естественного”, или абсолютного нуля, которому соответствует полное отсутствие измеряемого свойства. Если область определения значений шкалы отношений положительна, то ее называют положительной шкалой отношений. Все допустимые преобразования для шкалы отношений исчерпываются функциями вида f(x) = kx; (k > 0), что указывает на высочайшие возможности шкалы отношений как инструмента обобщения [13, с. 207].
        Шкала отношений, как наиболее мощная, суммирует все возможности, которыми обладают менее мощные шкалы наименований, порядка и интервалов. На ней определены отношения эквивалентности, равенства, порядка, функции метрики и расстояния. На шкале отношений можно определить равенство и ранговый порядок величин, равенство интервалов и отношений между величинами. Возможность оценки отношения величин - наиболее важная отличительная черта этой шкалы, определившая ее название. 
        Известные примеры шкалы отношений: массы, длины; температурная шкала Кельвина. Они представляют образцы положительных шкал отношений. На шкале отношений определены все арифметические операции, и к ее значениям применимы любые статистические процедуры.

Требование инвариантности (адекватности) выводов. Выяснение типов используемых шкал необходимо для адекватного выбора методов анализа данных. Основополагающим требованием является независимость выводов от того, какой именно шкалой измерения воспользовался исследователь (среди всех шкал, переходящих друг в друга при допустимых преобразованиях). Например, если речь о длинах, то выводы не должны зависеть от того, измерены ли длины в метрах, аршинах, саженях, футах или дюймах.

Другими словами, выводы должны быть инвариантны относительно группы допустимых преобразований шкалы измерения. Только тогда их можно назвать адекватными, т.е. избавленными от субъективизма исследователя, выбирающего определенную шкалу из множества шкал заданного типа, связанных допустимыми преобразованиями.

Требование инвариантности выводов накладывает ограничения на множество возможных алгоритмов анализа данных. В качестве примера рассмотрим порядковую шкалу. Одни алгоритмы анализа данных позволяют получать адекватные выводы, другие - нет. Например, в задаче проверки однородности двух независимых выборок алгоритмы ранговой статистики (т.е. использующие только ранги результатов измерений) дают адекватные выводы, а статистики Крамера-Уэлча и Стьюдента - нет. Значит, для обработки данных, измеренных в порядковой шкале, критерии Смирнова и Вилкоксона можно использовать, а критерии Крамера-Уэлча и Стьюдента - нет.

Выбор средних величин в соответствии со шкалами измерения

Требование инвариантности является достаточно сильным. Из многих алгоритмов анализа статистических данных ему удовлетворяют лишь некоторые. Покажем это на примере сравнения средних величин.

60)  Среднее по Коши, результат сравнения которых устойчив в порядковой шкале.

При допустимом преобразовании шкалы значение средней величины, очевидно, меняется. Но выводы о том, для какой совокупности среднее больше, а для какой - меньше, не должны меняться (в соответствии с требованием инвариантности выводов, принятом как основное требование в теории измерений). Сформулируем соответствующую математическую задачу поиска вида средних величин, результат сравнения которых устойчив относительно допустимых преобразований шкалы.

Пусть f(X₁, X₂,...,X_n) - среднее по  Коши. Пусть среднее по первой совокупности меньше среднего по второй совокупности:

 f(Y₁, Y₂,...,Y_n) <  f(Z₁, Z₂,...,Z_n).  

Тогда согласно теории измерений для устойчивости результата сравнения средних необходимо, чтобы для любого допустимого преобразования g из группы допустимых преобразований в соответствующей шкале было справедливо также неравенство

 f(g(Y₁), g(Y₂),...,g(Y_n)) <  f(g(Z₁), g(Z₂),...,g(Z_n)),  

т.е. среднее преобразованных значений из первой совокупности также было меньше среднего преобразованных значений для второй совокупности. Причем сформулированное условие должно быть верно для любых двух совокупностей Y₁, Y₂,...,Y_n и Z₁, Z₂,...,Z_n. И, напомним, для любого допустимого преобразования. Средние величины, удовлетворяющие сформулированному условию, назовем допустимыми (в соответствующей шкале). Согласно теории измерений только такими средними можно пользоваться при анализе мнений экспертов и иных данных, измеренных в рассматриваемой шкале.

          С помощью математической теории, развитой в монографии [7], удается описать вид допустимых средних в основных шкалах. Сразу ясно, что для данных, измеренных в шкале наименований, в качестве среднего годится только мода.

61) Средние по Колмогорову. Естественная система аксиом (требований к средним величинам) приводит к так называемым ассоциативным средним. Их общий вид нашел в 1930 г. А.Н. Колмогоров [9]. Теперь их называют «средними по Колмогорову».

Для чисел X₁, X₂,...,X_n средним по Колмогорову является

G{(F(X₁) + F(X₂) +...+ F(X_n))/n},

где F - строго монотонная функция (т.е. строго возрастающая или строго убывающая), G - функция, обратная к F. Среди средних по Колмогорову - много хорошо известных персонажей. Так, если F(x) = x, то среднее по Колмогорову - это среднее арифметическое, если F(x) = ln x, то среднее геометрическое, если F(x) = 1/x, то среднее гармоническое, если F(x) = x², то среднее квадратическое, и т.д. (в последних трех случаях усредняются положительные величины).

Среднее по Колмогорову - частный случай среднего по Коши. С другой стороны, такие популярные средние, как медиана и мода, нельзя представить в виде средних по Колмогорову. В статье [10] впервые доказаны следующие утверждения.

Теорема 2. В шкале интервалов из всех средних по Колмогорову допустимым является только среднее арифметическое.

Таким образом, среднее геометрическое или среднее квадратическое температур (в шкале Цельсия), потенциальных энергий или координат точек не имеют смысла. В качестве среднего надо применять среднее арифметическое. А также можно использовать медиану или моду.

Теорема 3. В шкале отношений из всех средних по Колмогорову допустимыми являются только степенные средние с и среднее геометрическое.

Есть ли средние по Колмогорову, которыми нельзя пользоваться в шкале отношений? Конечно, есть. Например, с F(x) = e^x.

Замечание 1. Среднее геометрическое является пределом степенных средних при .

Замечание 2. Теоремы 1 и 2 справедливы при выполнении некоторых внутриматематических условий регулярности. Доказательства теорем 1-3 приведены в монографии [7]. Перенос на случай взвешенных средних дан в статье [11].

62) Показатели разброса:

- Размах вариации

R = X_max - X_min

• Межквартельное расстояние

X([0,75n]) - X([0,25n])

• Среднее абсолютное линейное отклонение

D_ср = (1/n)* ∑ / X_i – X_ср / (сумма модуля)

d = (1/n)*

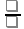
• Дисперсия

S² = (1/n)* ∑ ( X_i - X_ср )²

Особая роль дисперсии

Особую роль при интерпретации играют сведения о дисперсии измерений. Знание оценок дисперсии позволяет правильно задать вес каждого измерения при инверсии.

63)Внутригрупповая и межгрупповая дисперсия. Разложение общей дисперсии на внутригрупповую и межгрупповую. Однофакторный дисперсионный анализ и распределение Фишера.

Межгрупповая дисперсия (факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних  от общей средней:

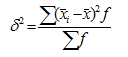
Внутригрупповая дисперсия (частная, остаточная, случайная)  отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы (хi) от средней арифметической этой группы (xср) (групповой средней) и может быть исчислена как:

1. простая дисперсия  2. взвешенная дисперсия

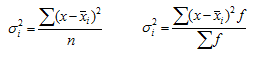
На основании внутригрупповой дисперсии по каждой группе  можно определить общую среднюю из внутригрупповых дисперсий:

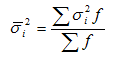
Разложение дисперсий Фишера:

n*k*S² = n*∑(S²(j) + n*k*S₁²)

Однофакторный дисперсионный анализ

Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак.

Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.

Для этих выборок предполагают, что они имеют разные выборочные средние и  одинаковые выборочные дисперсии. Поэтому необходимо ответить на вопрос, оказал ли этот фактор существенное влияние на разброс выборочных средних или разброс является следствием случайностей, вызванных небольшими объемами выборок. Другими словами если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).

Пусть  – i – элемент  ( )  -выборки (), гдеm – число выборок, nk – число данных в -выборке. Тогда – выборочное среднее -выборки определяется по формуле

.

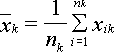          Общее среднее вычисляется по формуле

 

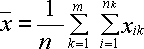, где 

 

          Основное тождество дисперсионного анализа имеет следующий вид:

,

где Q₁ – сумма квадратов отклонений выборочных средних  от общего среднего  (сумма квадратов отклонений между группами); Q₂ – сумма квадратов отклонений наблюдаемых значений  от выборочной средней  (сумма квадратов отклонений внутри групп); Q – общая сумма квадратов отклонений наблюдаемых значений от общего среднего.

          Расчет этих сумм квадратов отклонений осуществляется по следующим формулам:

 

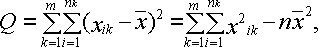
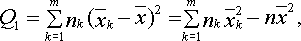
В качестве критерия необходимо воспользоваться критерием Фишера:

 

.

 

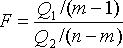Если расчетное значение критерия Фишера будет меньше, чем табличное значение  – нет оснований считать, что независимый фактор оказывает влияние на разброс средних значений, в противном случае, независимый фактор оказывает существенное влияние на разброс средних значений (λ– уровень  значимости, уровень риска, обычно для экономических задач λ=0,05).

Недостаток однофакторного анализа: невозможно выделить те выборки, которые отличаются от других. Для этой цели необходимо использовать метод Шеффе или проводить парные сравнения выборок.

РАСПРЕДЕЛЕНИЕ ФИШЕРА

(F-РАСПРЕДЕЛЕНИЕ) — распределение, заданное функцией плотности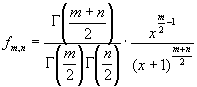; x > 0, где Γ(x) — гамма-функция; параметры m и n называются числами степеней свободы. Если X₁,. . ., X_m; Y₁, . . ., Y_n — независимые случайные величины, распределенные по нормальному закону, с параметрами (0, σ), то величина 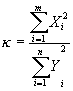распределена по закону Фишера.Математическое ожидание 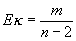для n > 2. Дисперсия случайной величины

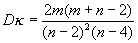для n> 4. Р. Ф. используется при решении многих геол. задач, в частности для выявления роли факторов, определяющих рудоносностьтого или иного объекта, в задачах, связанных с подсчетом запасов.

64)Выборочный и теоретический линейные парные коэффициенты корреляции К.Пирсона и их св-ва

Выборочный коэффициент корреляции

Понятие корреляции является одним из основных понятий теории вероятностей и математической статистики, оно было введено Гальтоном и Пирсоном.

Закон природы или общественного развития может быть представлен описанием совокупности взаимосвязей. Если эти зависимости стохастичны, а анализ осуществляется по выборке из генеральной совокупности, то данная область исследования относится к задачам стохастического исследования зависимостей, которые включают в себя корреляционный, регрессионный, дисперсионный и ковариационный анализы. В данном разделе рассмотрена теснота статистической связи между анализируемыми переменными, т.е. задачи корреляционного анализа.

В качестве измерителей степени тесноты парных связей между количественными переменными используются коэффициент корреляции (или то же самое "коэффициент корреляции Пирсона") и корреляционное отношение.

Пусть при проведении некоторого опыта наблюдаются две случайные величины и, причем одно и то же значениевстречаетсяраз,раз, одна и та же пара чисел (наблюдаетсяраз. Все данные записываются в виде таблицы, которую называют корреляционной.

Выборочный коэффициент корреляции r определяется как

, 

где , - выборочные средние, определяющиеся следующим образом:

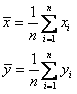
Свойства коэффициента корреляции r

• r изменяется в интервале от —1 до +1.

• Знак r означает, увеличивается ли одна переменная по мере того, как увеличивается другая (положительный r), или уменьшается ли одна переменная по мере того, как увеличивается другая (отрицательный r).

• Величина r величина указывает, как близко расположены точки к прямой линии. В частности, если r = +1 или r= —1, то имеется абсолютная (функциональная) корреляция по всем точкам, лежащим на линии (практически это маловероятно); если 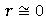, то линейной корреляции нет (хотя может быть нелинейное соотношение). Чем ближе r к крайним точкам (±1), тем больше степень линейной связи.

• Коэффициент корреляции r безразмерен, т. е. не имеет единиц измерения.

• Величина r обоснованна только в диапазоне значений x и y в выборке. Нельзя заключить, что он будет иметь ту же величину при рассмотрении значений x или y, которые значительно больше, чем их значения в выборке.

• x и y могут взаимозаменяться, не влияя на величину r ().

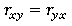• Корреляция между x и у не обязательно означает соотношение причины и следствия.

представляет собой долю вариабельности у, которая обусловлена линейным соотношением с x.

65. Выборочный коэффициент ранговой корреляции Спирмена.

Коэффициент корреляции Спирмена (Spearman rank correlation coefficient) — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги. Коэффициент инвариантен по отношению к любому монотонному преобразованию шкалы измерения.

Вычисление корреляции Спирмена:

Коэффициент корреляции Спирмена вычисляется по формуле:

,^[1] где - ранг наблюденияв ряду,- ранг наблюденияв ряду.

Коэффициент принимает значения из отрезка. Равенствоуказывает на строгую прямую линейную зависимость,на обратную.

66. Временные ряды (ряды динамики). Тренд, периодические колебания, случайные отклонения. Моментные и интервальные ряды. Полные и неполные ряды. Ряды абсолютных показателей и ряды относительных показателей. Графики.

Ряды динамики — это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Ряды динамики позволяют выявить закономерности развития изучаемых явлений. Ряды динамики содержат два вида показателей. Показатели времени (годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.). Показатели уровней ряда.

Интервальные ряды динамики

Уровни интервального ряда характеризуют результат изучаемого процесса за период времени: производство или реализация продукции ( за год, квартал, месяц и др. периоды), число принятых на работу, число родившихся и.т.п. Уровни интервального ряда можно суммировать. При этом получаем такой же показатель за более длительные интервалы времени.

Средний уровень в интервальных рядах динамики () исчисляется по формулесредней арифметическойпростой:

• y — уровни ряда (y₁, y₂ ,...,y_n),

• n — число периодов (число уровней ряда).