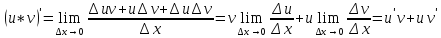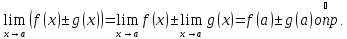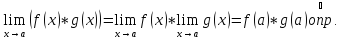M_zadania_1_2
.docxТеоремы
-
Теорема о единственности сходящейся последовательности
Если предел числовой последовательности существует и конечен, то он единственен
Предположим,
что существуют и конечны
 и
и
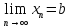 .
Пусть
.
Пусть
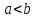 ,
тогда интервалы
,
тогда интервалы
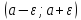 и
и
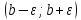 ,
где, например,
,
где, например,
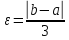 должны одновременно содержать все члены
числовой последовательности, кроме
конечного их числа, что невозможно, так
как эти интервалы не имеют общих точек.
Предположение неверное
должны одновременно содержать все члены
числовой последовательности, кроме
конечного их числа, что невозможно, так
как эти интервалы не имеют общих точек.
Предположение неверное
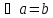
![]()
-
Теорема об ограниченности сходящейся последовательности
Любая сходящаяся последовательность ограничена
По
условию
 сходится
сходится
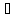 существует конечный
существует конечный
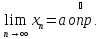 для
для
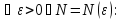 для
для
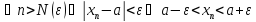 для
для
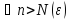 .
.
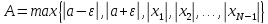 .
Тогда
.
Тогда
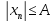 для
для
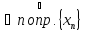 ограничена
ограничена
-
Теорема о локальной ограниченности функции, имеющей конечный предел
Если существует
и конечен
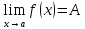 ,
то функция
,
то функция
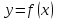 - локально ограниченная
- локально ограниченная
По
условию существует и конечен
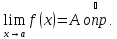 для
для
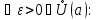 для
для
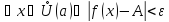 .
Пусть
.
Пусть
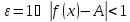 для
для
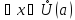 .
.
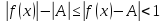 для
для
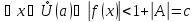 для
для
 - локально ограниченная.
- локально ограниченная.
-
Теорема о сохранении функцией знака своего предела
Если существует
и конечен
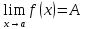 и
и
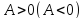 ,
то
,
то
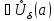 такая, что для
такая, что для

По
условию существует и конечен
 для
для
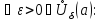 для
для
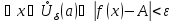 .
.
-
Пусть по условию
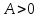 .
Возьмём
.
Возьмём
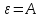 ,
тогда
,
тогда
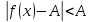 ;
;
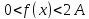 для
для
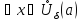
-
Пусть по условию
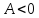 .
Возьмём
.
Возьмём
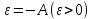 ,
тогда
,
тогда
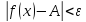 ;
;
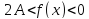 для
для
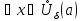
-
Теорема о предельном переходе в неравенстве
Если существуют
и конечны
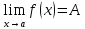 и
и
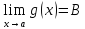 и для
и для
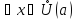 выполняется неравенство
выполняется неравенство
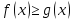 ,
то
,
то
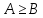
По
условию
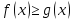 для
для
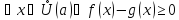 для
для
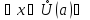 (По теореме о сохранении знака своего
предела)
(По теореме о сохранении знака своего
предела)
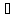
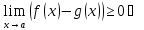
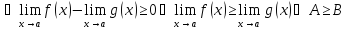
-
Теорема о пределе промежуточной функции
Если существуют
и конечны
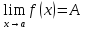 и
и
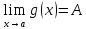 и
и
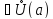 такая, что для
такая, что для
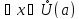 выполняется неравенство
выполняется неравенство
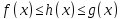 ,
то
,
то
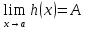
По
условию существуют и конечны
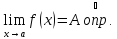 для
для
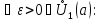 для
для
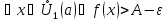 ;
;
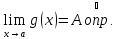 для
для
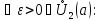 для
для
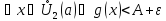 .
Рассмотрим
.
Рассмотрим
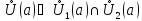 .
Тогда для
.
Тогда для
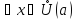 выполняется неравенство
выполняется неравенство
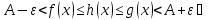
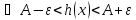 для
для
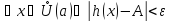 для
для
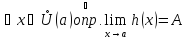
-
Теорема о пределе произведения функций
Если существуют
и конечны
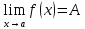 и
и
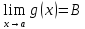 ,
то
,
то

По
условию существуют и конечны
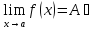 (По теореме
о связи функций, её предела и бесконечно
малой)
(По теореме
о связи функций, её предела и бесконечно
малой)
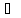
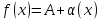 ,
где
,
где
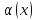 - бесконечно малая
при
- бесконечно малая
при
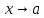 функция;
функция;
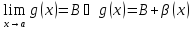 ,
где
,
где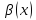 - бесконечно малая при
- бесконечно малая при
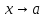 функция.
функция.
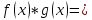
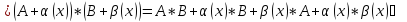
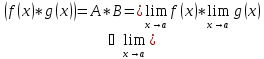
-
Теорема о пределе сложной функции
Если существует
и конечен
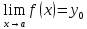 ,
причём
,
причём
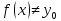 в
в
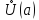 и существует и конечен
и существует и конечен
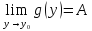 ,
то существует и конечен
,
то существует и конечен
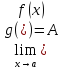
По
условию существуют и конечны
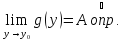 для
для
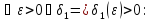 для
для
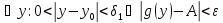 ;
;
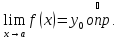 для
для
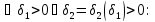 для
для
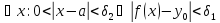 для
для
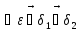 .
Для
.
Для
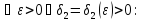 для
для
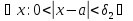

-
Доказательство первого замечательного предела
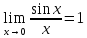
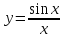 - чётная
- чётная
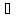 пределы слева и справа совпадают.
пределы слева и справа совпадают. 
Рассмотрим
предел функции справа:
 .
.
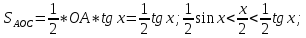
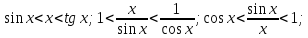
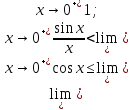
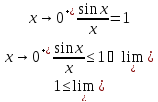
-
Теорема о связи функции, её предела и бесконечно малой
Если существует
и конечен
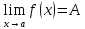 ,
то
,
то
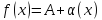 ,
где
,
где
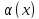 - бесконечно малая при
- бесконечно малая при
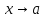 функция и наоборот, если
функция и наоборот, если
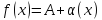 ,
где
,
где
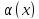 - бесконечно малая при
- бесконечно малая при
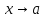 функция, то
функция, то
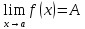
Необходимость:
По условию существует и конечен
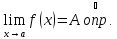 для
для
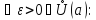 для
для
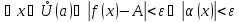 для
для
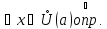
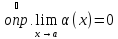 ,
где
,
где
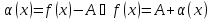
Достаточность:
По условию
 ,
где
,
где
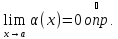 для
для
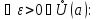 для
для
 ,
где
,
где
 для
для
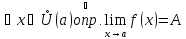
-
Теорема о произведении бесконечно малой функции на ограниченную
Если
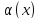 - бесконечно малая при
- бесконечно малая при
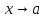 функция,
функция,
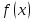 - ограниченная функция, то
- ограниченная функция, то
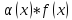 - бесконечно малая при
- бесконечно малая при
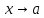 функция
функция
По
условию
 - бесконечно малая при
- бесконечно малая при
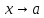 функция
функция
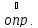 для
для
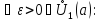 для
для
 - ограниченная функция
- ограниченная функция
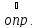
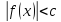 ,
где
,
где
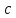 -
-
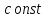 ,
для
,
для
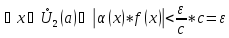 для
для
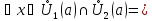
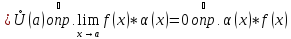 - бесконечно малая
при
- бесконечно малая
при
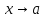 функция
функция
-
Теорема о связи между бесконечно большой и бесконечно малой
Если
 - бесконечно малая при
- бесконечно малая при
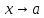 функция,
функция,
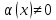 ,
то
,
то
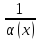 - бесконечно большая при
- бесконечно большая при
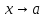 функция. Если
функция. Если
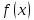 - бесконечно большая при
- бесконечно большая при
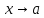 функция, то
функция, то
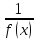 - бесконечно малая при
- бесконечно малая при
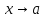 функция
функция
-
По условию
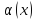 - бесконечно малая при
- бесконечно малая при
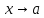 функция
функция
 для
для
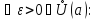 для
для
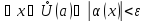 ;
;
 .
.
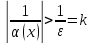 для
для
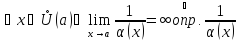 - бесконечно большая при
- бесконечно большая при
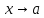 функция
функция -
По условию
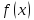 - бесконечно большая при
- бесконечно большая при
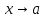 функция
функция
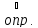 для
для
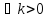
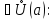 для
для
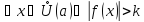 .
Рассмотрим
.
Рассмотрим
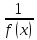 :
:
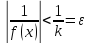 для
для
 - бесконечно малая при
- бесконечно малая при
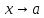 функция
функция
-
Теорема о замене бесконечно малой на эквивалентную под знаком предела
Если бесконечно
малые функции
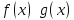 при
при
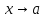 и
и
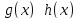 при
при
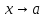 ,
не равные нулю в
,
не равные нулю в
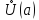 ,
то
,
то
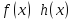 при
при
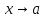
По
условию
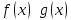 при
при
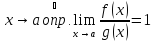 ;
;
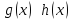 при
при
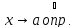
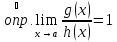 .
.
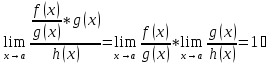
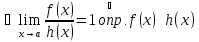 при
при
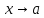
-
Теорема о необходимом и достаточном условии эквивалентности бесконечно малых
(Бесконечно малые
функции
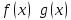 при
при
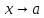 )
⇔
)
⇔
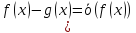 и
и
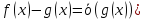
Необходимость:
По условию
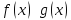 при
при
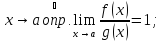
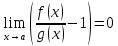 ;
;
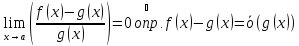 .
По условию
.
По условию
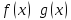 при
при
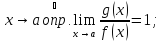
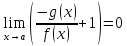 ;
;
 .
.
Достаточность:
По условию
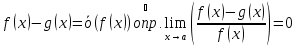 ;
;
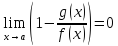 ;
;
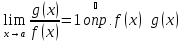 при
при
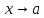 .
По условию
.
По условию
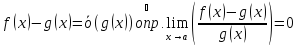 ;
;
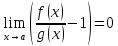 ;
;
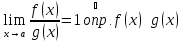 при
при
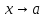 .
.
-
Теорема о сумме конечного числа бесконечно малых разных порядков
Если
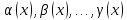 - бесконечно малые при
- бесконечно малые при
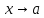 функции, то
функции, то
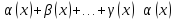 при
при
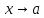 ,
где
,
где
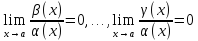
Рассмотрим

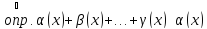 при
при
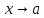
-
Теорема о непрерывности суммы, произведения и частного непрерывных функций
Если функции
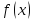 и
и
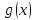 непрерывны в точке
непрерывны в точке
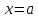 ,
то функции
,
то функции
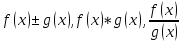 ,
где в последнем
,
где в последнем
 ,
непрерывны в точке
,
непрерывны в точке
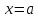
По
условию
 непрерывна в точке
непрерывна в точке
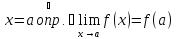 .
По условию
.
По условию
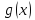 непрерывна в точке
непрерывна в точке
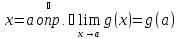 .
.
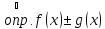 непрерывна в точке
непрерывна в точке
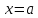
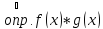 непрерывна в точке
непрерывна в точке
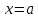
-
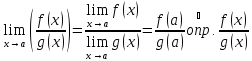 непрерывна при
непрерывна при
 в точке
в точке
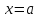
-
Теорема о непрерывности сложной функции
Если функция
 непрерывна в точке
непрерывна в точке
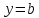 ,
а функция
,
а функция
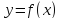 непрерывна в точке
непрерывна в точке
 ,
причём
,
причём
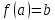 ,
то сложная функция
,
то сложная функция
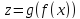 непрерывна в точке
непрерывна в точке
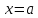
По
условию
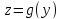 непрерывна в точке
непрерывна в точке
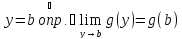 .
По условию
.
По условию
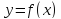 непрерывна в точке
непрерывна в точке
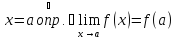 .
.
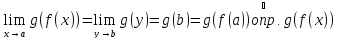 непрерывна в точке
непрерывна в точке
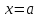
-
Теорема о сохранении знака непрерывной функции в окрестности точки
Если функция
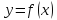 непрерывна в точке
непрерывна в точке
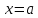 и
и
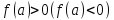 ,
то
,
то
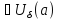 ,
в которой
,
в которой
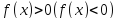
По
условию
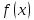 непрерывна в точке
непрерывна в точке
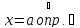 конечный
конечный
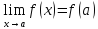 .
.
-
Пусть
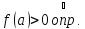 для
для
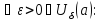 для
для
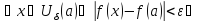
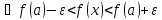 ,
где пусть, например,
,
где пусть, например,

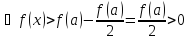 для
для
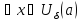 .
.
-
Пусть
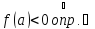 конечный
конечный
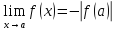 .
Заменим
.
Заменим
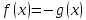 ,
тогда
,
тогда
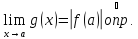 для
для
 для
для

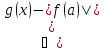 ,
где пусть, например,
,
где пусть, например,
 .
Вернёмся к прежней записи:
.
Вернёмся к прежней записи:
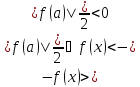 для
для
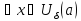 .
.
-
Теорема о непрерывности элементарных функций. Доказательство непрерывности функции
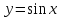
Основные элементарные
функции
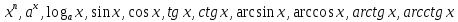 непрерывны в своей области определения.
непрерывны в своей области определения.
Функция
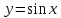 непрерывна в
непрерывна в
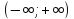
По
определению
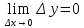 ,
где
,
где
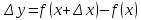 ,
,
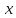 -
-
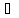 точка
точка
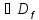 .
.
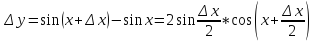 .
.
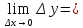
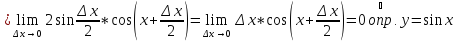 непрерывна в
непрерывна в
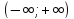
-
Свойства функций, непрерывных на отрезке
-
Первая теорема Вейерштрасса: Если функция
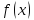 непрерывна на
непрерывна на
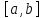 ,
то она ограничена на этом отрезке
,
то она ограничена на этом отрезке -
Вторая теорема Вейерштрасса: Если функция
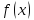 непрерывна на
непрерывна на
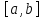 ,
то она достигает хотя бы в одной точке
этого отрезка свои максимальное и
минимальное значения
,
то она достигает хотя бы в одной точке
этого отрезка свои максимальное и
минимальное значения -
Первая теорема Больцано - Коши: Если функция
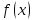 непрерывна на
непрерывна на
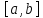 и
и
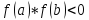 ,
то существует хотя бы одна точка
,
то существует хотя бы одна точка
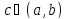 ,
в которой
,
в которой
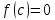
-
Вторая теорема Больцано - Коши: Если функция
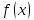 непрерывна на
непрерывна на
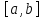 и
и
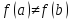 ,
то существует точка
,
то существует точка
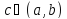 такая, что
такая, что
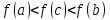 или
или
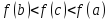
-
Теорема о непрерывности обратной функции: Если функция
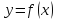 непрерывна и строго монотонна на
непрерывна и строго монотонна на
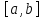 ,
то существует обратная функция
,
то существует обратная функция
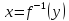 строго монотонная на
строго монотонная на
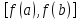
-
Определение точки разрыва функции. Классификация точек разрыва
Точка
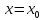 ,
в которой нарушается хотя бы одно из
условий непрерывности функции, называется
точкой разрыва функции
,
в которой нарушается хотя бы одно из
условий непрерывности функции, называется
точкой разрыва функции
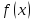 ,
а сама функция называется разрывной в
этой точке.
,
а сама функция называется разрывной в
этой точке.
-
Точка
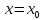 называется точкой разрыва I
рода, если
называется точкой разрыва I
рода, если
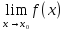 не существует, но существуют и конечны
не существует, но существуют и конечны
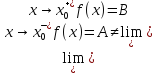
-
Точка
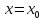 называется точкой устранимого разрыва,
если
называется точкой устранимого разрыва,
если
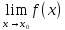 существует, но или
существует, но или
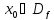 ,
или
,
или
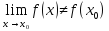
-
Точка
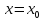 ,
в которой хотя бы один из односторонних
пределов функции в этой точке не
существует (в частности равен ∞),
называется точкой разрыва II
рода
,
в которой хотя бы один из односторонних
пределов функции в этой точке не
существует (в частности равен ∞),
называется точкой разрыва II
рода -
Точка
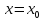 ,
в которой хотя бы один из односторонних
пределов функции в этой точке равен ∞,
называется точкой разрыва II
рода с бесконечным скачком
,
в которой хотя бы один из односторонних
пределов функции в этой точке равен ∞,
называется точкой разрыва II
рода с бесконечным скачком
-
Необходимое и достаточное условие существования наклонной асимптоты
Прямая
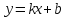 есть правая (левая) наклонная асимптота
графика функции
есть правая (левая) наклонная асимптота
графика функции
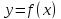 тогда и только тогда, когда существуют
и конечны
тогда и только тогда, когда существуют
и конечны
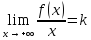 и
и
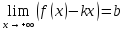

Необходимость:
По условию
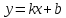 - правая наклонная асимптота
- правая наклонная асимптота
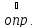
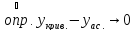 при
при
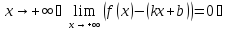
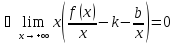 ,
где
,
где
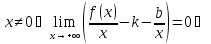
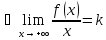 .
Из первого предела:
.
Из первого предела:
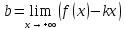
Достаточность:
По условию существует и конечен
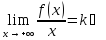
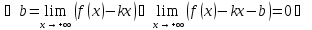
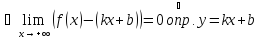 - правая наклонная
асимптота
- правая наклонная
асимптота
-
Необходимое и достаточное условие дифференцируемости функции в точке
Для того, чтобы
функция
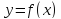 была дифференцируема в точке
была дифференцируема в точке
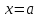 необходимо и достаточно, чтобы в этой
точке функция имела конечную производную,
то есть существует конечный
необходимо и достаточно, чтобы в этой
точке функция имела конечную производную,
то есть существует конечный
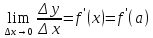
Необходимость:
По условию функция
 дифференцируема в точке
дифференцируема в точке

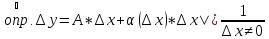 ,
где
,
где
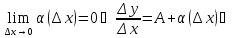 (По теореме о связи функции, её предела
и бесконечно малой)
(По теореме о связи функции, её предела
и бесконечно малой)
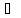
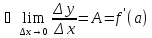
Достаточность:
По условию существует конечный
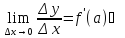 (По теореме о связи функции, её предела
и бесконечно малой)
(По теореме о связи функции, её предела
и бесконечно малой)
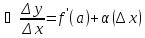 ,
где
,
где
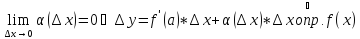 дифференцируема в точке
дифференцируема в точке
-
Теорема о связи дифференцируемости и непрерывности функции
Если функция
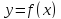 дифференцируема в точке
дифференцируема в точке
 ,
то она непрерывна в этой точке
,
то она непрерывна в этой точке
По
условию функция
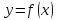 дифференцируема в точке
дифференцируема в точке
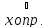
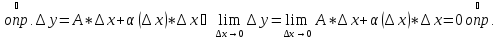
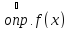 непрерывна в точке
непрерывна в точке
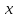
-
Теорема о производной произведения двух дифференцируемых функций
Если функции
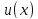 и
и
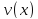 дифференцируемы в точке
дифференцируемы в точке
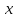 ,
то функция
,
то функция
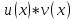 дифференцируема в точке
дифференцируема в точке
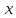 и
и
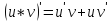
По
условию
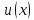 и
и
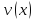 дифференцируемы в точке
дифференцируемы в точке
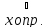 существуют и конечны
существуют и конечны
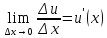 и
и
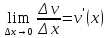 .
.
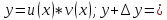
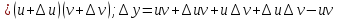 .
.