
M_zadania_1_2
.docx-
Теорема о производной частного двух дифференцируемых функций
Если функции
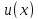 и
и
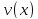 дифференцируемы в точке
дифференцируемы в точке
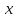 ,
то функция
,
то функция
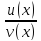 дифференцируема в точке
дифференцируема в точке
 и
и
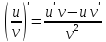 ,
где
,
где
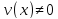
По
условию
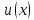 и
и
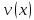 дифференцируемы в точке
дифференцируемы в точке
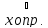 существуют и конечны
существуют и конечны
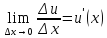 и
и
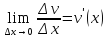 .
.
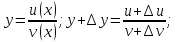
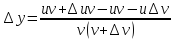 .
.
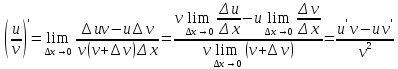 ,
где
,
где
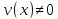
-
Теорема о производной сложной функции
Если функция
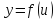 дифференцируема в точке
дифференцируема в точке
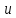 и функция
и функция
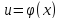 дифференцируема в точке
дифференцируема в точке
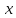 ,
то сложная функция
,
то сложная функция
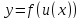 дифференцируема в точке
дифференцируема в точке
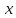 и
и
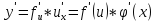
По
условию
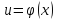 дифференцируема в точке
дифференцируема в точке
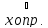 существует конечный
существует конечный
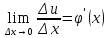 ;
;
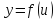 дифференцируема в точке
дифференцируема в точке
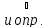 существует конечный
существует конечный
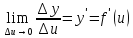 .
.
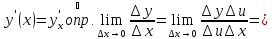
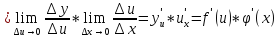 ,
где из
,
где из
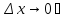 (По определению непрерывности функции)
(По определению непрерывности функции)
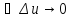
-
Теорема о производной обратной функции
Если строго
монотонная в
 функция
функция
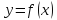 дифференцируема в точке
дифференцируема в точке
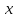 ,
то обратная функция
,
то обратная функция
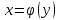 дифференцируема в точке
дифференцируема в точке
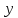 и
и
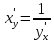
По условию
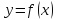 дифференцируема в точке
дифференцируема в точке
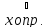 существует конечный
существует конечный
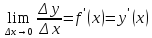
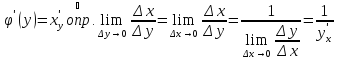 ,
где
,
где
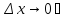 (По определению непрерывности функции)
(По определению непрерывности функции)
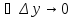
-
Свойство инвариантности формы записи дифференциала первого порядка
Дифференциал
функции
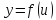 не зависит от того, является ли
не зависит от того, является ли
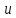 независимой переменной или функцией
другой независимой переменной
независимой переменной или функцией
другой независимой переменной
-
Пусть
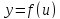 ,
где
,
где
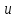 - независимая переменная.
- независимая переменная.
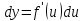 (По опр.)
(По опр.) -
Пусть
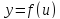 ,
где
,
где
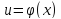 .
По правилу дифференцирования сложной
функции:
.
По правилу дифференцирования сложной
функции:
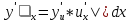 ;
;
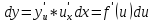
-
Теорема Ферма
Если функция
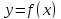 дифференцируема в точке
дифференцируема в точке
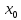 и точка
и точка
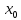 - точка локального экстремума функции,
то
- точка локального экстремума функции,
то
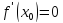
По
условию функция
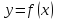 дифференцируема в точке
дифференцируема в точке
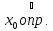 существует конечный
существует конечный
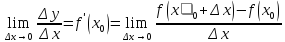 .
Пусть
.
Пусть
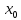 - точка локального максимума
- точка локального максимума
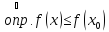 для
для
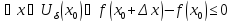
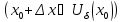
-
Пусть
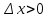 .
.
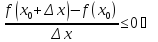 (По теореме о предельном переходе в
неравенстве)
(По теореме о предельном переходе в
неравенстве)
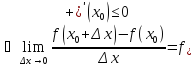
-
Пусть
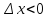 .
.
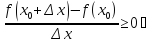 (По теореме о предельном переходе в
неравенстве)
(По теореме о предельном переходе в
неравенстве)
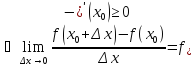
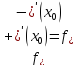 ,
так как по условию
,
так как по условию
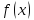 дифференцируема в точке
дифференцируема в точке
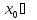

-
Теорема Ролля
Если функция
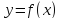 непрерывна на
непрерывна на
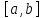 ,
дифференцируема в
,
дифференцируема в
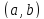 и
и
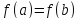 ,
то существует по крайней мере одна точка
,
то существует по крайней мере одна точка
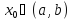 ,
в которой
,
в которой

По
условию
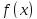 непрерывна на
непрерывна на
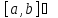 (По второй теореме Вейерштрасса)
(По второй теореме Вейерштрасса)
 функция
функция
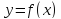 достигает на этом отрезке свои минимальное
и максимальное значения.
достигает на этом отрезке свои минимальное
и максимальное значения.
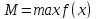 ;
;
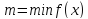 .
Возьмём случаи:
.
Возьмём случаи:
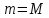 и
и
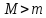 .
.
-
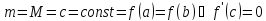 для
для
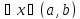
-
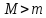 :
:
-
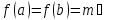 своё максимальное
значение функция достигает в точке
своё максимальное
значение функция достигает в точке
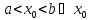 - точка локального экстремума. По условию
функция
- точка локального экстремума. По условию
функция
 дифференцируема в точке
дифференцируема в точке
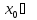 (По теореме Ферма)
(По теореме Ферма)
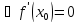
-
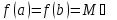 своё минимальное
значение функция достигает в точке
своё минимальное
значение функция достигает в точке
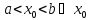 - точка локального экстремума. По условию
функция
- точка локального экстремума. По условию
функция
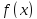 дифференцируема в точке
дифференцируема в точке
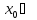 (По теореме Ферма)
(По теореме Ферма)
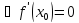
-
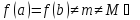 своё минимальное
и максимальное значения функция
достигает внутри отрезка
своё минимальное
и максимальное значения функция
достигает внутри отрезка
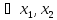 - точки локального экстремума. По условию
функция
- точки локального экстремума. По условию
функция
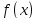 дифференцируема в точке
дифференцируема в точке
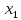 и
и
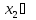 (По теореме Ферма)
(По теореме Ферма)
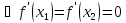
-
Теорема Лагранжа
Если функция
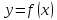 непрерывна на
непрерывна на
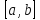 и дифференцируема в
и дифференцируема в
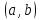 ,
то существует хотя бы одна точка
,
то существует хотя бы одна точка
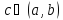 такая, что
такая, что
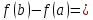
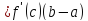
Обозначим
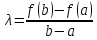 и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию
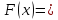
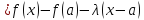 .
.
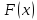 непрерывна на
непрерывна на
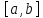 ,
дифференцируема в
,
дифференцируема в
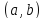 ,
,
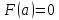 ,
,
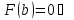 (По теореме Ролля)
(По теореме Ролля)
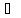 существует хотя бы одна точка
существует хотя бы одна точка
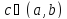 такая, что
такая, что
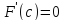 .
.
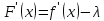 ;
;
 ;
;

-
Теорема Коши
Если функции
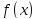 и
и
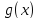 непрерывны на
непрерывны на
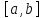 ,
дифференцируемы в
,
дифференцируемы в
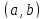 и
и
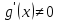 для
для
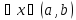 ,
то существует хотя бы одна точка
,
то существует хотя бы одна точка
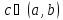 такая, что
такая, что
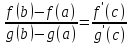
Пусть
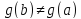 так как если бы
так как если бы
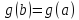 ,
то функция
,
то функция
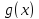 удовлетворяла бы условиям теоремы Ролля
удовлетворяла бы условиям теоремы Ролля
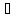 существует точка
существует точка
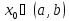 ,
,
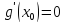 ,
что противоречит условию теоремы: по
условию
,
что противоречит условию теоремы: по
условию
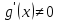 .
.
Обозначим
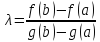 и рассмотрим вспомогательную функцию
и рассмотрим вспомогательную функцию
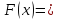
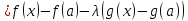 .
.
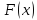 непрерывна на
непрерывна на
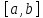 ,
дифференцируема в
,
дифференцируема в
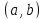 ,
,
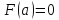 ,
,
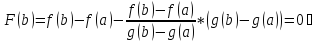 (По теореме Ролля)
(По теореме Ролля)
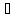 существует хотя бы одна точка
существует хотя бы одна точка
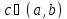 такая, что
такая, что
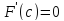 .
.
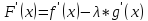 ;
;
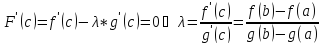
-
Теорема Лопиталя - Бернулли для предела отношения двух бесконечно малых функций
Если функции
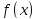 и
и
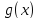 удовлетворяют условиям:
удовлетворяют условиям:
-
Бесконечно малые при
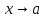 (бесконечно большие при
(бесконечно большие при
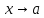 )
) -
Дифференцируемы в
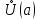 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
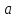
-
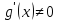 для
для
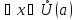 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
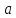
-
Существует
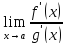
то существует
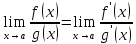
Пусть
по условию
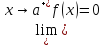 ,
,
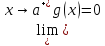 .
Доопределим функцию до непрерывности
в
.
Доопределим функцию до непрерывности
в
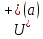 :
:
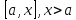 .
Пусть
.
Пусть
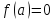 и
и
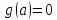 ,
тогда
,
тогда
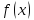 и
и
 непрерывны на
непрерывны на
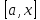 ,
дифференцируемы в
,
дифференцируемы в
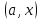 и
и
 в
в
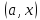 по условию
по условию
 (По теореме Коши)
(По теореме Коши)
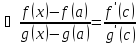 ,
где
,
где
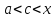 ,
,
 ,
,
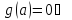
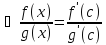 ;
;
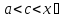 если
если
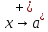 ,
то
,
то
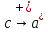 ;
по условию существует
;
по условию существует
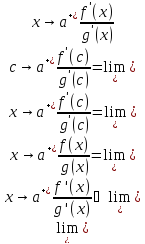
-
Сравнение роста показательной, степенной и логарифмической функций на бесконечности
При
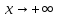 :
:
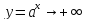 ,
,
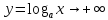 ,
,

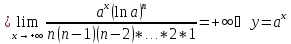 растёт быстрее
растёт быстрее
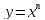 при
при
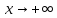
-
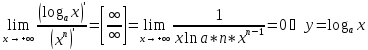 растёт медленнее
любой положительной степени
растёт медленнее
любой положительной степени
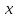
-
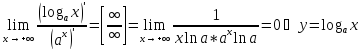 растёт медленнее
на
растёт медленнее
на
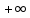 функции
функции
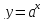
36-37. Формула Тейлора
Пусть
функция
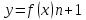 раз дифференцируема в
раз дифференцируема в
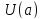
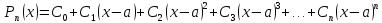 - разложение
многочлена по степеням
- разложение
многочлена по степеням

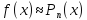 ,
то есть
,
то есть
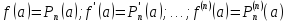
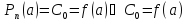
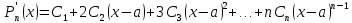
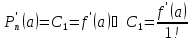
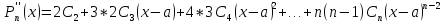
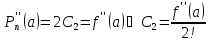
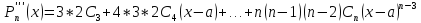
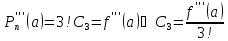
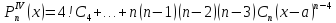
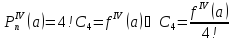
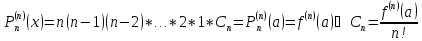
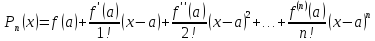 - многочлен Тейлора
- многочлен Тейлора
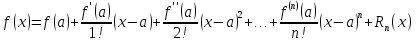 - формула Тейлора
- формула Тейлора
-
Формула Тейлора с остаточным членом в форме Лагранжа
Если функция
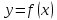 имеет в
имеет в
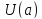 непрерывное производное до
непрерывное производное до
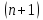 -го
порядка, то для
-го
порядка, то для
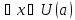 существует точка
существует точка
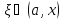 такая, что
такая, что
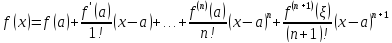
Обозначим
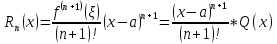 ,
,
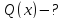
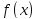 запишем в следующем
виде:
запишем в следующем
виде:
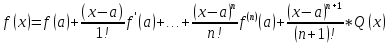
Рассмотрим
вспомогательную функцию, где
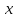 ,
,
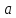 - фиксированные. Вместо
- фиксированные. Вместо
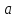 подставляем
подставляем
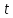 :
:
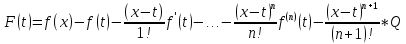
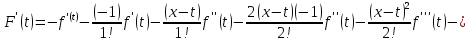
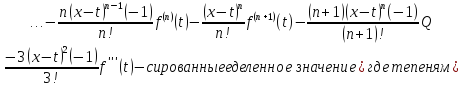
После
сокращений остаётся выражение:
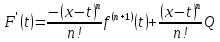
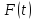 дифференцируема
в
дифференцируема
в
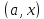 ;
;
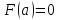 ;
;
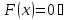 (По теореме Ролля)
(По теореме Ролля)
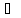
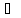 существует точка
существует точка
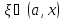 ;
;
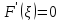
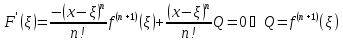
Таким
образом
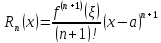
-
Формула Тейлора с остаточным членом в форме Пеано
По
теореме о формуле Тейлора с остаточным
членом в форме Лагранжа
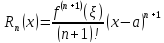 ,
,
 или
или
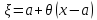 ,
где
,
где
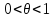
Уменьшая
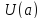 получим, что функция
получим, что функция
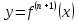 непрерывна на
непрерывна на
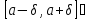 (По первой теореме
Вейерштрасса)
(По первой теореме
Вейерштрасса)
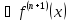 ограничена на этом отрезке, то есть
ограничена на этом отрезке, то есть
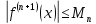 ,
где
,
где
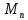 - число, не зависящее от
- число, не зависящее от
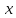 ,
но зависящее от
,
но зависящее от
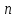 .
Тогда
.
Тогда
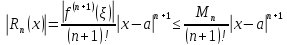 .
Исследуем
.
Исследуем
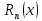 при
при
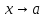 :
:
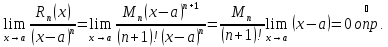
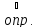
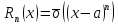
-
Формула Маклорена для функции
 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
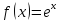
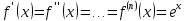
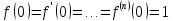
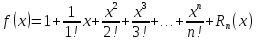 ,
где
,
где
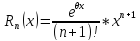 ,
,
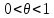
-
Формула Маклорена для функции
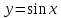 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
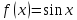 ;
;
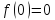
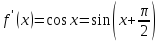 ;
;
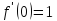
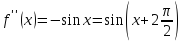 ;
;
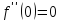
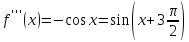 ;
;
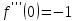
 ;
;
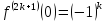
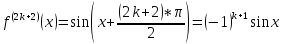 ;
;

 ,
,
где
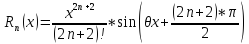 ,
,
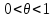
-
Формула Маклорена для функции
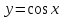 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
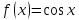 ;
;
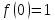
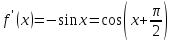 ;
;
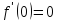
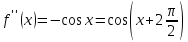 ;
;
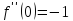
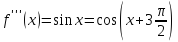 ;
;
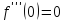
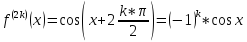 ;
;

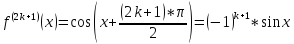 ;
;
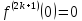
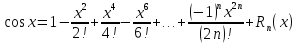
где
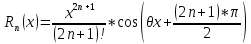 ,
,
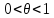
-
Формула Маклорена для функции
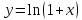 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
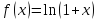 ;
;
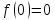
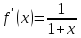 ;
;
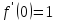
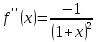 ;
;
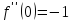
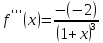 ;
;
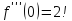
 ;
;
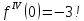
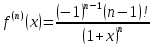 ;
;
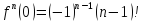
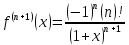 ;
;
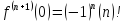
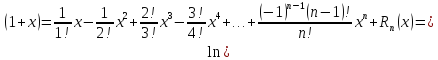
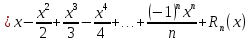 ,
где
,
где
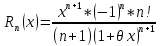 ,
,
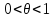
-
Формула Маклорена для функции
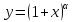 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
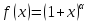 ;
;
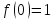
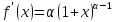 ;
;
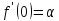
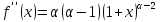 ;
;
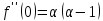
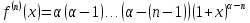 ;
;
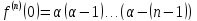

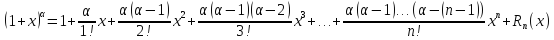 ,
,
где
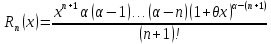 ,
,
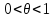
-
Необходимое и достаточное условие неубывания дифференцируемой функции
Для того, чтобы
дифференцируемая в
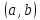 функция
функция
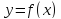 не убывала, необходимо и достаточно,
чтобы
не убывала, необходимо и достаточно,
чтобы
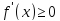 для
для
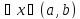
Необходимость:
По условию функция
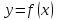 не убывает в
не убывает в
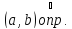
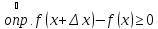 при
при
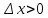 ;
;
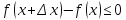 при
при
 ;
по условию
;
по условию
 дифференцируема в
дифференцируема в
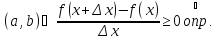 существует конечный
существует конечный
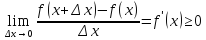 для
для
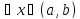
Достаточность:
Пусть по условию
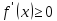 для
для
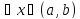 .
Возьмём
.
Возьмём
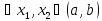 такие, что
такие, что
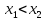 .
По условию
.
По условию
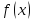 дифференцируема в
дифференцируема в
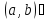
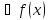 непрерывна на
непрерывна на
 ,
,
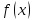 дифференцируема в
дифференцируема в
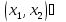 (По теореме Лагранжа)
(По теореме Лагранжа)
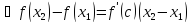 ,
где
,
где
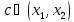 ;
;
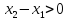 ;
;
 по условию, так как
по условию, так как
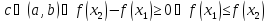 при
при
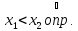
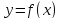 не убывает в
не убывает в

-
Необходимое и достаточное условие невозрастания дифференцируемой функции
Для того, чтобы
дифференцируемая в
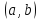 функция
функция
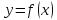 не возрастала, необходимо и достаточно,
чтобы
не возрастала, необходимо и достаточно,
чтобы
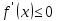 для
для
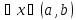
Необходимость:
По условию функция
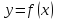 не возрастает в
не возрастает в
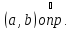
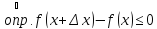 при
при
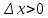 ;
;
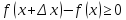 при
при
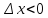 ;
по условию
;
по условию
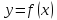 дифференцируема в
дифференцируема в
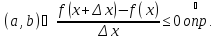 существует конечный
существует конечный
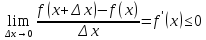 для
для
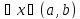
Достаточность:
Пусть по условию
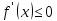 для
для
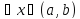 .
Возьмём
.
Возьмём
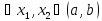 такие, что
такие, что
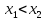 .
По условию
.
По условию
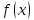 дифференцируема в
дифференцируема в

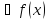 непрерывна на
непрерывна на
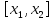 ,
,
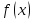 дифференцируема в
дифференцируема в
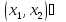 (По теореме Лагранжа)
(По теореме Лагранжа)
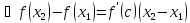 ,
где
,
где
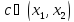 ;
;
 ;
;
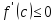 по условию, так как
по условию, так как
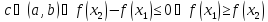 при
при
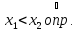
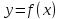 не возрастает в
не возрастает в
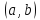
-
Достаточное условие возрастания дифференцируемой функции
Если функция
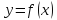 дифференцируема в
дифференцируема в
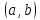 и для
и для
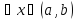
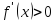 ,
то функция
,
то функция
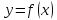 возрастает в этом интервале
возрастает в этом интервале

