
M_zadania_1_2
.docx
Пусть
по условию
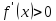 для
для
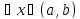 .
Возьмём
.
Возьмём
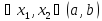 такие, что
такие, что
 .
По условию
.
По условию
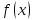 дифференцируема в
дифференцируема в
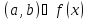 непрерывна на
непрерывна на
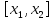 ,
,
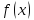 дифференцируема в
дифференцируема в
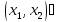 (По теореме Лагранжа)
(По теореме Лагранжа)
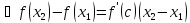 ,
где
,
где
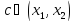 ;
;
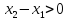 ;
;
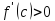 по условию, так как
по условию, так как
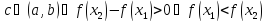 при
при

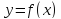 возрастает в
возрастает в
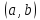
-
Достаточное условие убывания дифференцируемой функции
Если функция
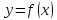 дифференцируема в
дифференцируема в
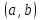 и для
и для
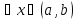
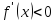 ,
то функция
,
то функция
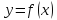 убывает в этом интервале
убывает в этом интервале
Пусть
по условию
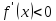 для
для
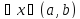 .
Возьмём
.
Возьмём
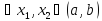 такие, что
такие, что
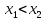 .
По условию
.
По условию
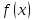 дифференцируема в
дифференцируема в
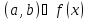 непрерывна на
непрерывна на
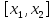 ,
,
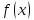 дифференцируема в
дифференцируема в
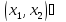 (По теореме Лагранжа)
(По теореме Лагранжа)
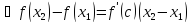 ,
где
,
где
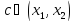 ;
;
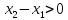 ;
;
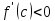 по условию, так как
по условию, так как
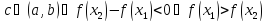 при
при
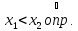
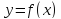 убывает в
убывает в
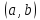
-
Первое достаточное условие экстремума (по первой производной)
Если функция
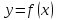 непрерывна в
непрерывна в
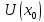 и дифференцируема в
и дифференцируема в
 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
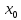 ,
,
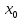 - критическая точка функции, и
- критическая точка функции, и
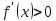 для
для
 ,
,
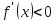 для
для
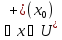 (
(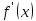 меняет знак с + на - при переходе через
точку
меняет знак с + на - при переходе через
точку
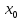 )
(
)
(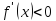 для
для
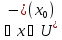 ,
,
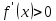 для
для
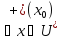 (
(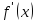 меняет знак с - на + при переходе через
точку
меняет знак с - на + при переходе через
точку
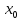 )),
то
)),
то
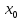 - точка локального максимума (минимума)
- точка локального максимума (минимума)
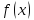
-
Пусть по условию
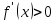 при
при
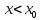 и
и
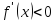 при
при
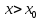
-
По условию
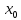 - критическая точка функции
- критическая точка функции
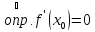 или
или
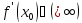 .
Возьмём
.
Возьмём
 такие, что
такие, что
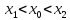
-
По условию
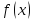 непрерывна в
непрерывна в
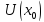 и дифференцируема в
и дифференцируема в
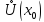 кроме, быть может, самой точки
кроме, быть может, самой точки
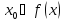 непрерывна на
непрерывна на
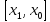 и
и
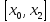 ,
,
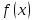 дифференцируема в
дифференцируема в
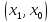 и
и
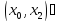 (По теореме Лагранжа)
(По теореме Лагранжа)
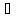
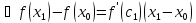 ,
,
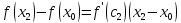 ,
где
,
где
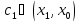 ,
,
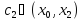 .
.
Рассмотрим
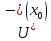 :
по условию
:
по условию
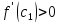 ,
,
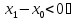
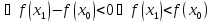 для
для
 ;
рассмотрим
;
рассмотрим
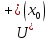 :
по условию
:
по условию
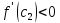 ,
,
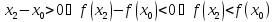 для
для
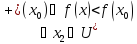 для
для
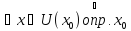 - точка локального максимума. Аналогично
для точки локального минимума
- точка локального максимума. Аналогично
для точки локального минимума
-
Второе достаточное условие экстремума (по второй производной)
Если в стационарной
точке
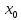 функция
функция
 дважды дифференцируема и
дважды дифференцируема и
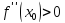 (
(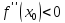 ),
то
),
то
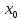 - точка локального минимума (максимума)
- точка локального минимума (максимума)
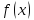
Пусть
по условию
 функция
функция
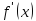 возрастает в
возрастает в
 ,
,
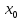 - стационарная точка по условию
- стационарная точка по условию
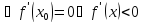 при
при
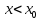 ,
,
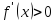 при
при
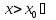 (По первому достаточному условию
экстремума)
(По первому достаточному условию
экстремума)
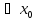 - точка локального минимума. Аналогично
для точки локального максимума
- точка локального минимума. Аналогично
для точки локального максимума
-
Достаточное условие выпуклости функций
Если функция
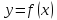 дважды дифференцируема в
дважды дифференцируема в
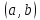 и
и
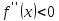
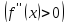 для
для
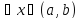 ,
то график функции имеет выпуклость,
направленную вверх (вниз) в
,
то график функции имеет выпуклость,
направленную вверх (вниз) в
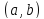
По
условию
 дифференцируема в
дифференцируема в
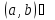 существует касательная к кривой в точках
существует касательная к кривой в точках
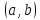 .
Пусть по условию
.
Пусть по условию
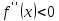 для
для
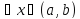 .
Возьмём
.
Возьмём
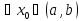 .
Докажем, что график функции лежит под
касательной, проведённой к кривой в
точке
.
Докажем, что график функции лежит под
касательной, проведённой к кривой в
точке
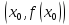 .
Уравнение касательной:
.
Уравнение касательной:
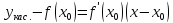 ,
,
 .
Вычитаем из
.
Вычитаем из
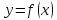 :
:
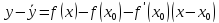 .
.
Функция
 удовлетворяет условиям теоремы Лагранжа
удовлетворяет условиям теоремы Лагранжа
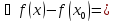
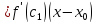 ,
где
,
где
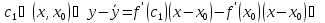
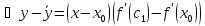 .
Функция
.
Функция
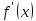 удовлетворяет условиям теоремы Лагранжа
удовлетворяет условиям теоремы Лагранжа
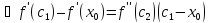 ,
где
,
где
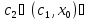
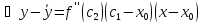 .
.
-
Рассмотрим
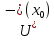 :
:
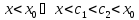 .
.
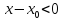 ;
;
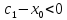 ;
по условию
;
по условию
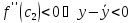 для
для
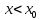
-
Рассмотрим
 :
:
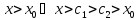 .
.
 ;
;
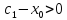 ;
по условию
;
по условию
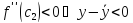 для
для
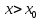
Таким
образом
 для
для
 график функции находится под касательной,
проведённой в точке
график функции находится под касательной,
проведённой в точке
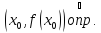 график функции имеет выпуклость,
направленную вверх в точке
график функции имеет выпуклость,
направленную вверх в точке
 ,
а так как
,
а так как
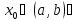
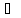 график функции
имеет выпуклость, направленную вверх
в
график функции
имеет выпуклость, направленную вверх
в
 .
.
Аналогично
для
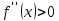
-
Необходимое условие точки перегиба
Если функция
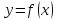 дважды дифференцируема в
дважды дифференцируема в
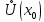 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
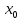 и
и
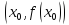 - точка перегиба графика функции, то
- точка перегиба графика функции, то
 или
или
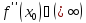 .
.
-
Пусть по условию
 дважды дифференцируема в точке
дважды дифференцируема в точке
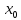 .
Предположим, что
.
Предположим, что
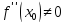
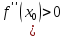 или
или
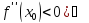 (По достаточному условию выпуклости
функции)
(По достаточному условию выпуклости
функции)
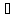 график функции имеет определённое
направление выпуклости в
график функции имеет определённое
направление выпуклости в
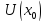 ,
что противоречит условию теоремы, так
как по условию
,
что противоречит условию теоремы, так
как по условию
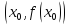 - точка перегиба
- точка перегиба
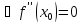
-
По условию
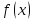 не является дважды дифференцируема в
точке
не является дважды дифференцируема в
точке
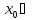
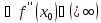
-
Достаточное условие точки перегиба
Если функция
 непрерывна в точке
непрерывна в точке
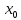 и дважды дифференцируема в
и дважды дифференцируема в
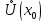 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки
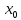 и
и
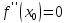 или
или
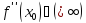 и существует касательная к графику
функции в точке
и существует касательная к графику
функции в точке
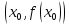 и
и
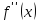 меняет знак при переходе через точку
меняет знак при переходе через точку
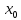 ,
то
,
то
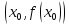 - точка перегиба
- точка перегиба
-
По условию
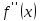 меняет знак. Пусть, например,
меняет знак. Пусть, например,
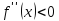 для
для
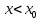 ;
;
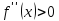 для
для
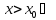 кривая выпукла вверх в
кривая выпукла вверх в
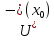 и кривая выпукла вниз в
и кривая выпукла вниз в
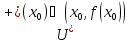 - точка перегиба.
- точка перегиба.
-
Аналогично при
 для
для
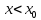 ;
;
 для
для
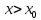
Определения
-
Число a называется пределом последовательности
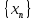 ,
если для любого сколь угодно малого
положительного
,
если для любого сколь угодно малого
положительного
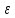 существует номер
существует номер
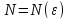 такой, что для всех номеров
такой, что для всех номеров
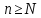 выполняется неравенство
выполняется неравенство
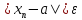 .
.
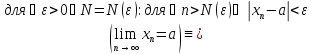
-
Пример предела по Коши:
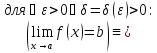
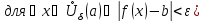
Пример
предела по Гейне:
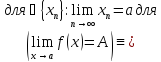
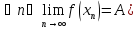
-
Окрестностью
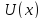 точки
точки
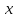 называют любой интервал, содержащий
эту точку.
называют любой интервал, содержащий
эту точку.
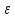 -окрестностью
точки
-окрестностью
точки
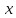 (при положительном
(при положительном
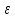 )
называют интервал
)
называют интервал
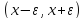
-
Окрестностью точки
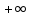 называют интервал вида
называют интервал вида
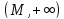 ,
где
,
где
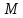 - произвольное действительное сколь
угодно большое число.
- произвольное действительное сколь
угодно большое число.
Окрестностью
точки
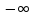 называют интервал вида
называют интервал вида
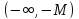 ,
где
,
где
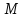 - произвольное действительное сколь
угодно большое число.
- произвольное действительное сколь
угодно большое число.
Окрестностью
точки
 называют объединение двух бесконечных
интервалов вида
называют объединение двух бесконечных
интервалов вида
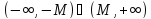 ,
где
,
где
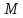 - произвольное действительное сколь
угодно большое число.
- произвольное действительное сколь
угодно большое число.
-
Если предел числовой последовательности существует и конечен, то он называется сходящейся.
Числовая
последовательность
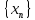 называется ограниченной, если она
ограничена и сверху и снизу.
называется ограниченной, если она
ограничена и сверху и снизу.
Числовая
последовательность
 называется возрастающей, если
называется возрастающей, если
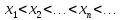 .
.
Числовая
последовательность
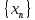 называется убывающей, если
называется убывающей, если
 .
.
Числовая
последовательность
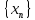 называется невозрастающей, если
называется невозрастающей, если
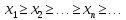 .
.
Числовая
последовательность
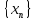 называется неубывающей, если
называется неубывающей, если
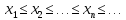 .
.
Невозрастающие и неубывающие последовательности называются монотонными.
Последовательность
 называется фундаментальной, если для
любого
называется фундаментальной, если для
любого
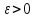 существует номер
существует номер
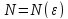 такой, что при любых
такой, что при любых
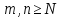 выполняется неравенство
выполняется неравенство
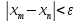 .
.
-
Функция
 называется бесконечно малой при
называется бесконечно малой при
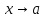 ,
если
,
если
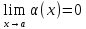 .
.
Функция
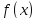 называется бесконечно большой при
называется бесконечно большой при
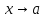 ,
если
,
если
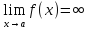 .
.
-
Две бесконечно малые при
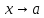 функции
функции
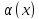 и
и
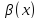 называются бесконечно малыми одного
порядка, если
называются бесконечно малыми одного
порядка, если
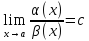 ,
где
,
где
 -
-
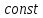 ,
,
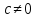 ,
,
 .
.
Две
бесконечно малые при
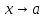 функции
функции
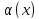 и
и
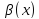 называются несравнимыми, если при
называются несравнимыми, если при
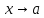 не существует ни конечного, ни бесконечного
предела отношения
не существует ни конечного, ни бесконечного
предела отношения
 .
.
Две
бесконечно малые при
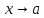 функции
функции
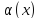 и
и
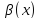 называются эквивалентными бесконечно
малыми, если
называются эквивалентными бесконечно
малыми, если
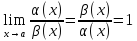 .
.
-
Если
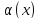 и
и
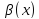 бесконечно малые при
бесконечно малые при
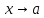 функции и
функции и
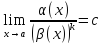 ,
,
где
 -
-
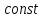 ,
,
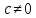 ,
,
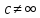 ,
то функция
,
то функция
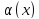 называется бесконечно малой функцией
порядка
называется бесконечно малой функцией
порядка
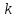 относительно
относительно
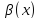 ,
а число
,
а число
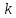 - порядком малости.
- порядком малости.
-
Если
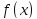 и
и
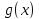 бесконечно большие при
бесконечно большие при
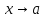 функции и
функции и
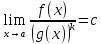 ,
,
где
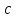 -
-
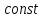 ,
,
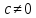 ,
,
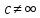 ,
то функция
,
то функция
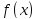 называется бесконечно большой функцией
порядка
называется бесконечно большой функцией
порядка
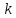 относительно
относительно
 ,
а число
,
а число
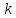 - порядком роста.
- порядком роста.
-
Приращением функции называют
 .
.
-
Функция
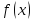 называется непрерывной в точке
называется непрерывной в точке
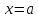 ,
если:
,
если:
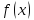 определена в точке
определена в точке
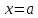 и в
и в
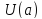 ,
существует
,
существует
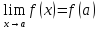 .
.
-
Функция
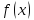 называется
непрерывной на интервале
называется
непрерывной на интервале
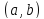 ,
если она непрерывна в каждой точке
этого интервала.
,
если она непрерывна в каждой точке
этого интервала.
Функция
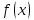 называется
непрерывной на отрезке
называется
непрерывной на отрезке
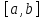 ,
если она непрерывна в интервале
,
если она непрерывна в интервале
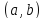 и непрерывна в точке
и непрерывна в точке
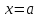 справа и в точке
справа и в точке
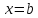 слева.
слева.
-
Точка
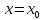 называется точкой разрыва функции
называется точкой разрыва функции
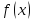 ,
если данная функция не является
непрерывной в точке
,
если данная функция не является
непрерывной в точке
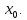
Точка
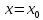 называется точкой устранимого разрыва
функции
называется точкой устранимого разрыва
функции
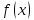 ,
если предел
,
если предел
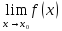 существует, но функция не определена в
этой точке или
существует, но функция не определена в
этой точке или
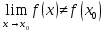 .
.
Точка
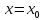 называется точкой разрыва I
рода, если
называется точкой разрыва I
рода, если
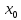 - точка разрыва функции
- точка разрыва функции
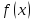 ,
и существуют конечные пределы
,
и существуют конечные пределы
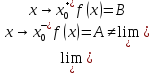 .
.
Точка
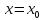 называется точкой разрыва II
рода, если хотя бы один из односторонних
пределов не существует (в частности
равен ∞).
называется точкой разрыва II
рода, если хотя бы один из односторонних
пределов не существует (в частности
равен ∞).
-
Пусть функция
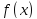 определена при
определена при
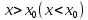 ,
и пусть
,
и пусть
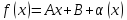 при
при
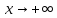
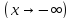 ,
где
,
где
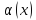 - бесконечно малая функция при
- бесконечно малая функция при
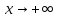
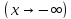 .
Тогда прямая
.
Тогда прямая
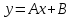 называется правой (левой) наклонной
асимптотой графика функции
называется правой (левой) наклонной
асимптотой графика функции
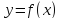 .
.
-
Пусть функция
 определена в окрестности точки
определена в окрестности точки
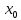 ,
и пусть
,
и пусть
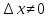 таково, что
таково, что
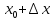 принадлежит указанной окрестности.
Если существует предел
принадлежит указанной окрестности.
Если существует предел
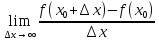 ,
то он называется производной функции
,
то он называется производной функции
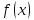 в
точке
в
точке
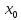 .
.
-
Пусть функция
 определена в правосторонней (левосторонней)
окрестности точки
определена в правосторонней (левосторонней)
окрестности точки
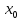 ,
то в точке
,
то в точке
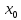 можно рассмотреть предел
можно рассмотреть предел
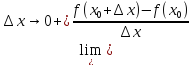
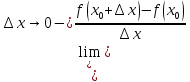 ,
который в случае его существования
называется правосторонней (левосторонней)
производной функции
,
который в случае его существования
называется правосторонней (левосторонней)
производной функции
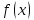 в точке
в точке
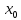 .
Левая и правая производные называются
односторонними.
.
Левая и правая производные называются
односторонними.
-
Пусть функция
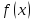 определена в окрестности точки
определена в окрестности точки
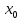 .
Эта функция называется дифференцируемой
в точке
.
Эта функция называется дифференцируемой
в точке
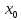 ,
если её приращение может быть представлено
в виде
,
если её приращение может быть представлено
в виде
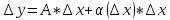 ,
где
,
где
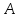 - некоторое число не зависящее от
- некоторое число не зависящее от
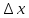 .
.
-
Пусть функция
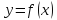 дифференцируема в точке
дифференцируема в точке
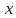 .
Тогда приращение этой функции может
быть записано в виде
.
Тогда приращение этой функции может
быть записано в виде
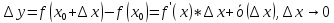 .
Дифференциалом
.
Дифференциалом
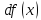 функции
функции
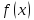 в точке
в точке
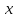 называется
называется
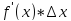 .
.
-
Производная n-го порядка определяется по индукции. Пусть
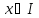 ,
и пусть в окрестности этой точки
определена производная (n-1)-го
порядка
,
и пусть в окрестности этой точки
определена производная (n-1)-го
порядка
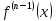 .
Тогда производная n-го
порядка
.
Тогда производная n-го
порядка
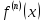 в точке
в точке
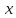 по определению есть
по определению есть
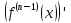 .
.
-
Дифференциал n-го порядка определяется по индукции. Пусть дифференциал (n-1)-го порядка уже определён, то дифференциал n-го порядка по определению есть
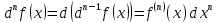 .
.
-
Функция
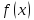 ,
определённая на промежутке
,
определённая на промежутке
 ,
называется возрастающей на этом
промежутке, если для любых точек
,
называется возрастающей на этом
промежутке, если для любых точек
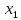 и
и
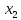 этого промежутка из неравенства
этого промежутка из неравенства
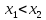 следует неравенство
следует неравенство
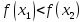 .
.
Функция
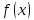 ,
определённая на промежутке
,
определённая на промежутке
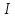 ,
называется невозрастающей на этом
промежутке, если для любых точек
,
называется невозрастающей на этом
промежутке, если для любых точек
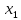 и
и
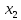 этого промежутка из неравенства
этого промежутка из неравенства
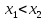 следует неравенство
следует неравенство
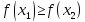 .
.
Функция
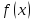 ,
определённая на промежутке
,
определённая на промежутке
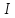 ,
называется убывающей на этом промежутке,
если для любых точек
,
называется убывающей на этом промежутке,
если для любых точек
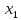 и
и
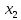 этого промежутка из неравенства
этого промежутка из неравенства
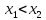 следует неравенство
следует неравенство
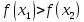 .
.
Функция
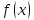 ,
определённая на промежутке
,
определённая на промежутке
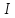 ,
называется неубывающей на этом промежутке,
если для любых точек
,
называется неубывающей на этом промежутке,
если для любых точек
 и
и
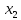 этого промежутка из неравенства
этого промежутка из неравенства
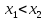 следует неравенство
следует неравенство
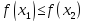 .
.
