
3. Сильно -однородные геометрии
Предположим,
что
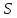 - сильно
- сильно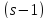 -однородная
геометрия
-однородная
геометрия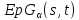 .
По лемме 1.2 число
.
По лемме 1.2 число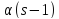 делит
делит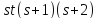 ,
поэтому
,
поэтому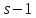 делит
делит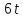 .
По лемме 1.3 точечный граф
.
По лемме 1.3 точечный граф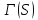 является псевдогеометрическим для
частичной геометрии
является псевдогеометрическим для
частичной геометрии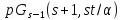 .
В частности, он сильно регулярен с
параметрами
.
В частности, он сильно регулярен с
параметрами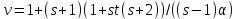 ,
,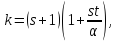 λ
λ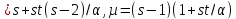 ,
и
,
и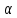 делит
делит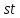 .
Далее, собственные значения графа
.
Далее, собственные значения графа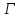 равны
равны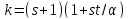 ,
, Можно считать, что
Можно считать, что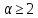 ,
поэтому
,
поэтому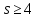 .
.
Лемма 3.1. Верны следующие утверждения:
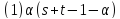 делит
делит
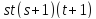 ;
;
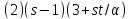 делит
делит
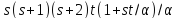 ;
;
 если
если
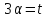 или
или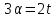 ,
то
,
то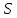 - одна из геометрий
- одна из геометрий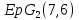 или
или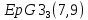 .
.
Доказательство.
Утверждения (1–2)-не что иное, как условия
целочисленности для
 и
и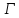 .
.
Пусть
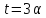 .
Тогда
.
Тогда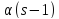 делит
делит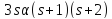 ,
поэтому
,
поэтому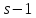 делит 18 и
делит 18 и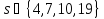 .
Кроме того,
.
Кроме того,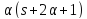 делит
делит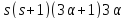 .
Вслучае
.
Вслучае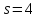 число
число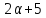 делит
делит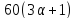 ,
поэтому
,
поэтому .
Противоречие с тем, что
.
Противоречие с тем, что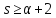 .
.
Если
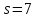 ,
то
,
то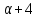 делит
делит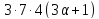 ,
поэтому
,
поэтому .
В этом случае заключение леммы выполняется.
.
В этом случае заключение леммы выполняется.
Если
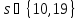 ,
то 27 делит
,
то 27 делит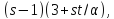 но не делит
но не делит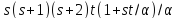 .
.
Пусть
теперь
 ,
,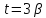 .
Тогда
.
Тогда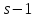 делит 18 и
делит 18 и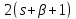 делит
делит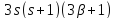 ,
поэтому
,
поэтому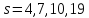 .
Таккак 27 делит
.
Таккак 27 делит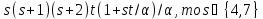 .
Если
.
Если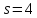 ,
то
,
то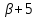 делит
делит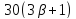 ,
поэтому
,
поэтому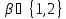 .
Но геометрия
.
Но геометрия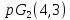 не существует, а
не существует, а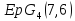 не удовлетворяет условию целочисленности.
не удовлетворяет условию целочисленности.
Если
 делит
делит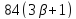 ,
поэтому
,
поэтому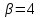 .
Противоречие с тем, что
.
Противоречие с тем, что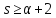 .
.
Лемма
3.2. Либо
 есть
есть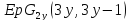 с нечетным
с нечетным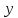 ,
либо
,
либо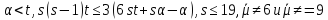 в графе
в графе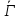 .
.
Доказательство.
Напомним, что
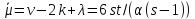 .
Если
.
Если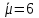 ,
то
,
то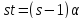 и
и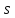 делит
делит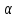 ,
противоречие.
,
противоречие.
Пусть
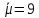 .
Тогда
.
Тогда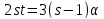 .
Следовательно, либо
.
Следовательно, либо ,
либо
,
либо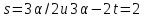 .
В первом случае по утверждению (2) леммы
3.1 число
.
В первом случае по утверждению (2) леммы
3.1 число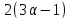 делит
делит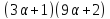 ,
поэтому
,
поэтому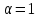 ,
противоречие. Во втором случае имеем
расширение частичной геометрии
,
противоречие. Во втором случае имеем
расширение частичной геометрии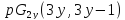 ,
и по утверждению (1) леммы 3.1число
,
и по утверждению (1) леммы 3.1число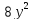 делит
делит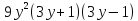 ,
поэтому
,
поэтому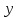 нечетно. В этом случае заключение леммы
выполняется.
нечетно. В этом случае заключение леммы
выполняется.
Пусть
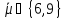 .
Используя оценку для числа лап в графе
.
Используя оценку для числа лап в графе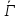 ,
имеем
,
имеем поэтому
поэтому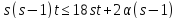 .
Значит,
.
Значит, не больше 0, поэтому
не больше 0, поэтому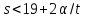 .
.
Если
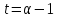 ,
то
,
то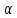 делит
делит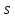 .
Следовательно,
.
Следовательно,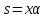 ,
а также
,
а также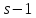 делит
делит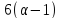 и
и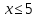 .
По утверждению (2) леммы 3.1 число
.
По утверждению (2) леммы 3.1 число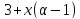 делит
делит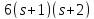 ,
значит,
,
значит,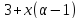 делит
делит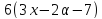 .
Для
.
Для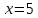 параметр
параметр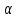 не больше 4, и
не больше 4, и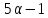 не делит
не делит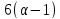 ,
противоречие. Для
,
противоречие. Для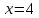 число
число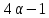 делит 9, а для
делит 9, а для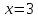 число
число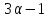 делит 4. В любом случае приходим к
противоречию. Наконец, для
делит 4. В любом случае приходим к
противоречию. Наконец, для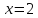 число
число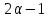 делит 3, и
делит 3, и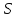 есть
есть .
Противоречие с леммой 1.4.
.
Противоречие с леммой 1.4.
Если
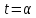 ,
то
,
то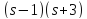 делит
делит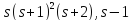 и
и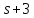 делят 12, поэтому
делят 12, поэтому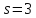 .
Но в этом случае
.
Но в этом случае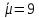 ,
противоречие.
,
противоречие.
Пусть
теперь
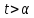 .
.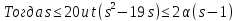 .
Если
.
Если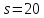 ,
то
,
то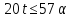 и
и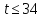 .
Далее,
.
Далее,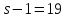 делит
делит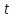 ,
поэтому
,
поэтому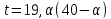 делит
делит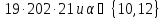 .
Но
.
Но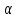 делит
делит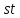 ,
поэтому
,
поэтому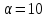 ,
противоречие с утверждением (2) леммы
3.1. Лемма доказана.
,
противоречие с утверждением (2) леммы
3.1. Лемма доказана.
Будем
предполагать, что
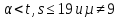 .
.
Лемма
3.3. Если
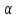 делит
делит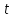 ,
то
,
то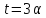 .
.
Доказательство.
Пусть
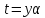 .
Тогда
.
Тогда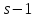 делит
делит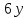 ,
и по утверждению (2) леммы 3.1 число
,
и по утверждению (2) леммы 3.1 число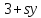 делит
делит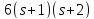 ,
поэтому
,
поэтому делит
делит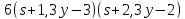 .
.
В
случае
 число
число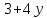 делит
делит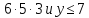 ,
поэтому
,
поэтому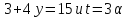 .
В случае
.
В случае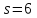 число
число делит
делит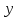 ,
,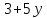 делит 6·7·8.
делит 6·7·8.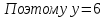 ,
и 11 не делит 7·8. В случае
,
и 11 не делит 7·8. В случае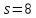 число
число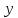 делится на 7 и
делится на 7 и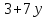 делит 6·9·10. Поэтому
делит 6·9·10. Поэтому и 24 не делит
и 24 не делит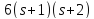 .
В случае
.
В случае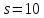 имеем y
имеем y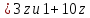 делит 11 · 12. Значит,
делит 11 · 12. Значит,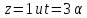 .
В случае
.
В случае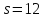 имеем
имеем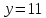 ,
и 45 не делит 13 · 14, противоречие.
,
и 45 не делит 13 · 14, противоречие.
Если
 четно, то либо 3 делит
четно, то либо 3 делит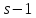 ,
либо
,
либо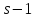 делит
делит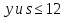 .
Следовательно,
.
Следовательно,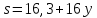 делит
делит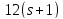 ,
поэтому
,
поэтому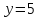 или 10, и
или 10, и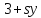 не делит
не делит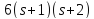 .
.
Значит,
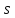 нечетно. Если
нечетно. Если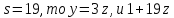 делит 3 · 5 · 7, противоречие.
делит 3 · 5 · 7, противоречие.
В
случае
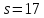 число
8 делит y и 3+17y делит 6 · 18 · 19, противоречие.
число
8 делит y и 3+17y делит 6 · 18 · 19, противоречие.
В
случае
 число 7 делит
число 7 делит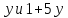 делит 2 · 16 · 17, противоречие.
делит 2 · 16 · 17, противоречие.
В
случае
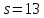 число
число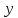 четно
четно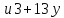 делит 3 · 7 · 15, противоречие.
делит 3 · 7 · 15, противоречие.
В
случае
 число 5 делит
число 5 делит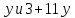 делит 6 · 12 · 13, противоречие.
делит 6 · 12 · 13, противоречие.
В
случае
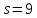 число 4 делит
число 4 делит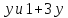 делит 5 · 11, противоречие.
делит 5 · 11, противоречие.
В
случае
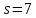 число
число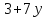 делит 6 · 8 · 9, поэтому
делит 6 · 8 · 9, поэтому .
.
В
случае
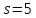 число
число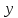 четно и
четно и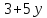 делит 3·3·7, поэтому
делит 3·3·7, поэтому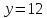 и в псевдогеометрическом графе для
и в псевдогеометрическом графе для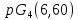 условия
целочисленности выполнены. Однако в
этом случае имеем
условия
целочисленности выполнены. Однако в
этом случае имеем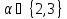 и в геометриях
и в геометриях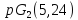 ,
,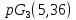 условия целочисленности нарушаются.
условия целочисленности нарушаются.
Лемма
3.4. Если
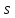 нечетно, то геометрия
нечетно, то геометрия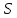 есть либо
есть либо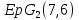 ,
либо
,
либо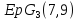 .
.
Доказательство.
Если
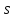 - простое число, то
- простое число, то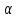 делит
делит ,
и ввиду лемм 3.1 и 3.3 заключение леммы
выполняется.
,
и ввиду лемм 3.1 и 3.3 заключение леммы
выполняется.
Пусть
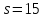 .
Тогда
.
Тогда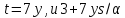 делит 6·16·17. Если 3 делит
делит 6·16·17. Если 3 делит делит 25 · 17, противоречие. Значит, 3 не
делит
делит 25 · 17, противоречие. Значит, 3 не
делит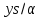 ,
и
,
и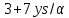 делит 25 · 17. Поэтому
делит 25 · 17. Поэтому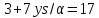 или 8 · 17. Значит,
или 8 · 17. Значит,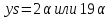 .
В любом случае s делит α, противоречие.
.
В любом случае s делит α, противоречие.
Пусть
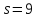 .
Тогда 4 делит
.
Тогда 4 делит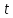 ,
и по лемме 3.3 число 3 делит
,
и по лемме 3.3 число 3 делит .
Следовательно,
.
Следовательно,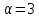 или 6, кроме того,
или 6, кроме того,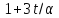 делит 5 · 11. Поэтому
делит 5 · 11. Поэтому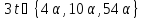 .
В первом случае
.
В первом случае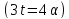 либо
либо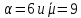 ,
либо
,
либо ,
и 11 не делит
,
и 11 не делит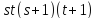 .
Во втором случае получимпротиворечие
с утверждением (2) леммы 3.1. В третьем
случае α
.
Во втором случае получимпротиворечие
с утверждением (2) леммы 3.1. В третьем
случае α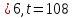 ,
противоречие с утверждением (1) леммы
3.1. Лемма доказана.
,
противоречие с утверждением (1) леммы
3.1. Лемма доказана.
В
леммах 3.5–3.8 будем предполагать, что
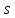 четно.
четно.
Лемма
3.5. Если
 взаимно просто с
взаимно просто с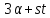 ,
то
,
то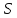 есть
есть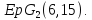
Доказательство.
Пусть
 взаимно просто с
взаимно просто с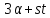 .
По лемме 3.1 число
.
По лемме 3.1 число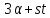 делит
делит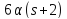 .
Тогда
.
Тогда и 3 делит
и 3 делит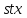 .
В случае
.
В случае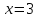 имеем
имеем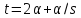 ,
противоречие. Поэтому
,
противоречие. Поэтому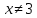 и 3 делит
и 3 делит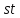 .
.
Пусть
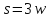 .
Тогда
.
Тогда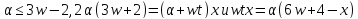 .
Так как
.
Так как делит
делит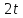 .
В случае
.
В случае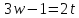 получим
получим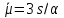 ,
поэтому
,
поэтому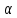 взаимно просто с
взаимно просто с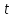 и
и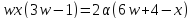 .
Отсюда
.
Отсюда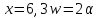 и число
и число не целое. Значит,
не целое. Значит,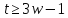 .
.
Если
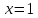 ,
то
,
то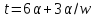 и
и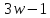 делит
делит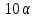 .
В случае
.
В случае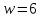 имеем
имеем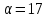 ,
противоречие. В случае
,
противоречие. В случае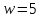 имеем
имеем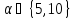 и 7 не делит
и 7 не делит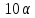 .
В случае
.
В случае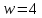 имеем
имеем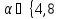 }
и 11 не делит
}
и 11 не делит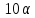 .
В случае
.
В случае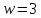 имеем
имеем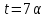 и 8 не делит
и 8 не делит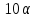 ,
поэтому α
,
поэтому α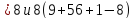 не делит
не делит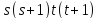 .
В случае
.
В случае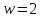 имеем
имеем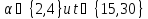 .
Так как
.
Так как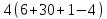 не делит
не делит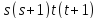 ,
то
,
то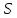 является расширением геометрии
является расширением геометрии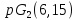 .
.
Если
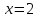 ,
то
,
то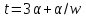 и
и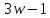 делит
делит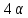 .
Поэтому α
.
Поэтому α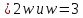 ,
противоречие с тем, что
,
противоречие с тем, что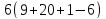 не
делит
не
делит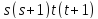 .
.
Если
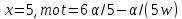 ,
противоречие.
,
противоречие.
Итак,
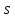 не делится на 3, поэтому 3 делит
не делится на 3, поэтому 3 делит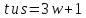 .
Тогда
.
Тогда
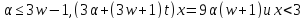 .
.
Если
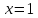 ,
то
,
то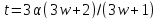 ,
противоречие. Если
,
противоречие. Если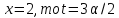 ,
,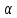 четно и
четно и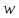 нечетно. Так как
нечетно. Так как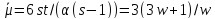 ,
то
,
то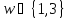 .
Если
.
Если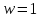 ,
то
,
то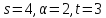 ,
противоречие с тем, что частичная
геометрия
,
противоречие с тем, что частичная
геометрия не существует. Если
не существует. Если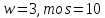 ,
,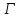 является псевдогеометрическим графом
для
является псевдогеометрическим графом
для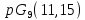 и нарушается условие целочисленности.
и нарушается условие целочисленности.
Лемма
3.6. Если
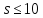 ,
то
,
то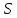 является геометрией
является геометрией
Доказательство.
Пусть
 .
Тогда
.
Тогда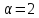 и
и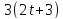 делит
делит кроме того, по лемме 3.5 простое число 5
делит
кроме того, по лемме 3.5 простое число 5
делит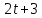 .
Следовательно,
.
Следовательно, не делит
не делит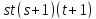 .
.
Пусть
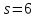 .
По лемме 3.5 число 7 делит
.
По лемме 3.5 число 7 делит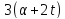 .
Если
.
Если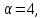 то
то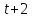 делится
на 7 и
делится
на 7 и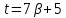 .
Далее,
.
Далее,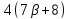 делит
делит )
и
)
и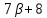 делит 126, противоречие.
делит 126, противоречие.
Если
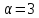 ,
то
,
то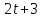 делится
на 7 и
делится
на 7 и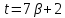 .
Далее,
.
Далее,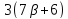 делит
делит и
и делит 84, поэтому
делит 84, поэтому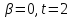 и
и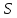 является
расширением геометрии
является
расширением геометрии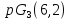 .
Но в этом случае по лемме 1.2 число
.
Но в этом случае по лемме 1.2 число должно быть четно, противоречие.
должно быть четно, противоречие.
Если
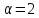 ,
то
,
то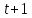 делится на 7 и
делится на 7 и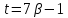 .
Далее,
.
Далее,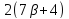 делит
делит и
и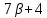 делит 21 · 20, поэтому
делит 21 · 20, поэтому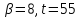 ,
противоречие с тем, что геометрия
,
противоречие с тем, что геометрия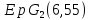 не удовлетворяет условию Крейна.
не удовлетворяет условию Крейна.
Пусть
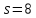 .
Так как
.
Так как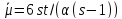 ,
то 7 делит
,
то 7 делит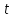 и
и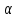 четно (так как
четно (так как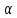 делит
делит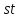 ,
но не делит
,
но не делит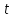 ).
По лемме 3.5 число 3 делит
).
По лемме 3.5 число 3 делит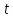 ,
поэтому
,
поэтому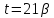 .
.
Если
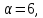 то
то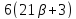 делит
делит и
и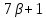 делит
делит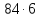 ,
поэтому
,
поэтому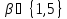 .
В случае
.
В случае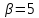 число
число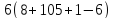 не делит
не делит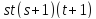 .
В случае
.
В случае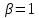 число
число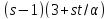 не делит
не делит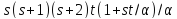 ,
противоречие.
,
противоречие.
Если
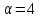 ,
то
,
то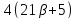 делит
делит делит
делит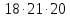 ,
поэтому
,
поэтому ,
противоречие. Если
,
противоречие. Если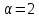 ,
то
,
то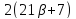 делит
делит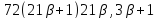 делит
делит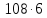 ,
поэтому
,
поэтому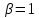 ,
противоречие с тем, что
,
противоречие с тем, что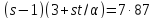 не делит
не делит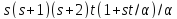 .
.
Пусть
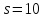 .
Тогда
.
Тогда для некоторого целого числа
для некоторого целого числа ,
и 11 делит
,
и 11 делит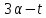 .
Поэтому
.
Поэтому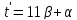 .
Если
.
Если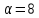 ,
то
,
то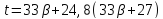 делит
делит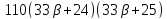 и
и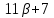 делит
делит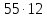 ,
противоречие.
,
противоречие.
Если
 ,
то
,
то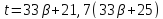 делит
делит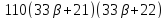 и
и делит
делит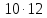 ,
противоречие.
,
противоречие.
Если
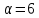 ,
то
,
то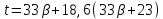 делит
делит и
и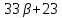 делит
делит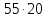 ,
противоречие.
,
противоречие.
Если
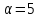 ,
то
,
то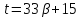 и
и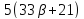 делит
делит и
и делит
делит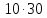 ,
противоречие.
,
противоречие.
Если
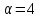 ,
то
,
то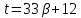 и
и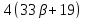 делит
делит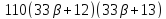 и
и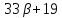 делит
делит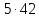 ,
противоречие.
,
противоречие.
Если
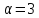 ,
то
,
то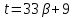 и
и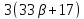 делит
делит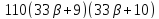 и
и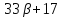 делит
делит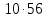 ,
противоречие.
,
противоречие.
Если
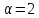 ,
то
,
то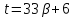 и
и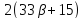 делит
делит и
и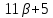 делит
делит ,
поэтому
,
поэтому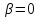 и
и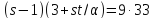 не делит
не делит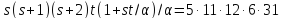 .
.
Лемма
3.7. Если
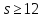 ,
то
,
то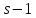 делит
делит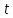 ,
и
,
и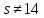 .
.
Доказательство.
Пусть
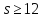 .
Если
.
Если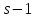 не делит
не делит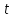 ,
то
,
то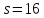 и 3 не делит
и 3 не делит .
Но в этом случае
.
Но в этом случае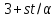 взаимно просто с 6, и
взаимно просто с 6, и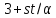 делит 17, противоречие.
делит 17, противоречие.
Пусть
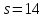 .
Тогда 13 делит
.
Тогда 13 делит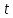 ,
и либо
,
и либо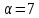 ,
либо
,
либо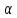 четно. Если
четно. Если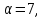 то
то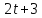 делит
делит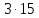 ,
противоречие.
,
противоречие.
Если
3 делит
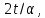 то
то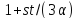 делит
делит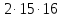 .
Но
.
Но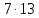 не делит
не делит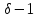 для любого делителя
для любого делителя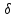 числа
числа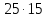 .
Значит, 3 не делит
.
Значит, 3 не делит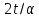 ,
и
,
и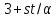 делит
делит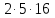 .
Как и выше, пришли к противоречию.
.
Как и выше, пришли к противоречию.
Лемма
3.8. Параметр
 меньше 12.
меньше 12.
Доказательство.
Пусть
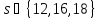 .
Согласно леммам 3.5, 3.7 число
.
Согласно леммам 3.5, 3.7 число делит
делит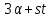 ,
и
,
и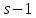 делит
делит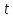 .
Если 3 не делит
.
Если 3 не делит ,
то
,
то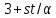 делит
делит .
Пусть
.
Пусть .
Тогда 3 делит
.
Тогда 3 делит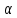 ,
и
,
и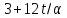 делит
делит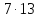 .
Значит,
.
Значит,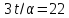 и
и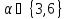 (
(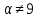 по лемме 1.2). Следовательно,
по лемме 1.2). Следовательно,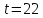 или 44, но в каждом случае
или 44, но в каждом случае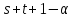 не делит
не делит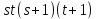 .
Если
.
Если ,
то
,
то делит 17, противоречие. Пусть
делит 17, противоречие. Пусть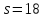 .
Тогда
.
Тогда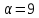 ,
и 3 не делит
,
и 3 не делит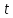 ,
так что
,
так что делит
делит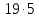 .
Противоречие с тем, что 17 делит
.
Противоречие с тем, что 17 делит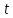 .
.
Таким
образом, 3 делит
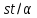 ,
и
,
и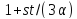 делит
делит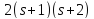 .
Пусть
.
Пусть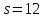 .
Тогда 11 делит
.
Тогда 11 делит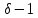 для некоторого делителя
для некоторого делителя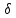 числа
числа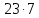 .
Поэтому
.
Поэтому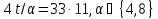 и
и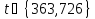 .
Но в первом случае нарушается условие
Крейна, а во втором число
.
Но в первом случае нарушается условие
Крейна, а во втором число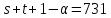 не делит
не делит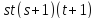 .
.
Пусть
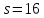 .
Тогда
.
Тогда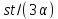 является четным, и
является четным, и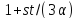 делит
делит .
Если
.
Если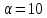 ,
то
,
то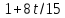 делит
делит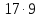 и
и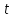 нечетно. Значит,
нечетно. Значит,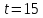 или
или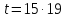 .
В любом из этих случаев
.
В любом из этих случаев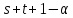 не делит
не делит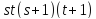 .
Поэтому 5 не делит
.
Поэтому 5 не делит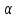 ,
и 5 делит
,
и 5 делит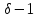 для некоторого
для некоторого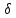 ,
являющегося делителем числа
,
являющегося делителем числа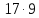 .
Следовательно,
.
Следовательно,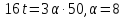 и
и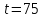 .
В этом случае
.
В этом случае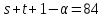 не делит
не делит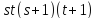 .
.
Пусть
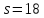 .
Тогда
.
Тогда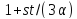 делит
делит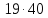 ,
и 17 делит
,
и 17 делит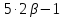 для
для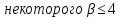 ,
противоречие. Лемма доказана.
,
противоречие. Лемма доказана.
Леммы 3.4, 3.6 и 3.8 доказывают теорему 2.
Список литературы
1. Cameron P. J., Hughes D. R., Pasini A. Extended generalized quadrangles // Geom. Dedicata. 1990. V. 35. P. 193–228.
2. Thas J. A. Some results on quadrics and newpartial geometries // Simon Stevin. 1981. V. 55. P. 129–139.
3. Hobart S. A., Hughes D. R. Extended partial geometries: nets and dual nets // Europ. J. Comb. 1990. V. 11. P. 357–372.
4.
Hobart S. A., Hughes D. R.
 withminimal µ. II //Geom. Dedicata. 1992.
withminimal µ. II //Geom. Dedicata. 1992.
V. 42. P. 129–138.
5. HughesD. R. Extended partial geometries: dual 2-design //Europ. J. Comb. 1990. V. 11. P. 459–472.
6. Seidel J. J. Strongly regular graphs with (−1,1,0) adjacency matrix having eigenvalue 3 // Linear Algebra&Appl. 1968. V. 1. P. 281–298.
7. Brouwer A. E., Lint J. H. van. Strongly regular graphs and partial geometries // Enumeration&Design / Eds. D. Jackson, S. Vanstone. NewYork: Academic Press, 1984. P. 85–122.
