
§ 2. Об однородных расширениях частичных геометрий.
Геометрия
 ранга 2 –
это система инцидентности
ранга 2 –
это система инцидентности
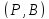 ,
где
,
где
 – множество точек,
– множество точек, – некоторый набор подмножеств
– некоторый набор подмножеств ,
называемых блоками. Два блока называютсяколлинеарными,
если они лежат в общем блоке. Если
,
называемых блоками. Два блока называютсяколлинеарными,
если они лежат в общем блоке. Если
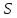 является геометрией ранга 2, то точечный
граф
является геометрией ранга 2, то точечный
граф – это граф с множеством вершин
– это граф с множеством вершин ,
в котором различные вершины смежны,
если они коллинеарны. Геометрия
,
в котором различные вершины смежны,
если они коллинеарны. Геометрия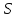 будет называтьсясвязной,
регулярной
и т.д., если граф
будет называтьсясвязной,
регулярной
и т.д., если граф
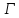 обладает соответствующими свойствами.
обладает соответствующими свойствами.
Пара
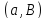 ,
из
,
из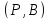 ,
называетсяфлагом,
если точка
,
называетсяфлагом,
если точка
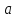 принадлежит блоку
принадлежит блоку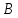 ,
иантифлагом
в противном случае. Если
,
иантифлагом
в противном случае. Если
 является антифлагом, то через
является антифлагом, то через обозначим число точек в
обозначим число точек в ,
коллинеарных
,
коллинеарных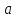 .
Геометрия называется
.
Геометрия называется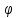 –однородной
(
–однородной
( – натуральное число), если для любого
антифлага
– натуральное число), если для любого
антифлага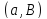 число
число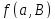 равно 0 или
равно 0 или ,
исильно
,
исильно
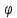 - однородной,
если это число всегда равно
- однородной,
если это число всегда равно
 .
.
Вычет
 геометрии
геометрии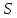 в точке
в точке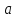 – это геометрия
– это геометрия
 ранга 2, где
ранга 2, где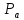 – множество всех точек, коллинеарных
– множество всех точек, коллинеарных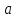 ,
и
,
и .
Пусть
.
Пусть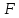 -
семейство геометрий ранга 2, и всякий
вычет
-
семейство геометрий ранга 2, и всякий
вычет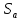 лежит в
лежит в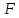 .
Тогда говорят, что S являетсярасширением
.
Тогда говорят, что S являетсярасширением
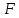 .
Геометрия
.
Геометрия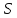 называетсятреугольной,
если для любых попарно коллинеарных
точек
называетсятреугольной,
если для любых попарно коллинеарных
точек
 найдется блок, содержащий все три точки
найдется блок, содержащий все три точки .
Точечный граф
.
Точечный граф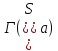 - это подграф
(возможно, собственный) графа,
индуцированного на
- это подграф
(возможно, собственный) графа,
индуцированного на
 графом
графом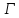 .
Заметим, что
.
Заметим, что для
любой точки
для
любой точки
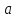 тогда и только тогда, когда геометрия
тогда и только тогда, когда геометрия треугольная.
треугольная.
Если
 -
различные точки геометрии
-
различные точки геометрии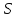 ,
то геометрия
,
то геометрия имеет множество точек
имеет множество точек и множество блоков
и множество блоков .
Положим
.
Положим (соответственно,
(соответственно,
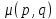 ),
если
),
если равно 1 (соответственно, 2) в точечном
графе
равно 1 (соответственно, 2) в точечном
графе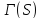 .
.
Блоки
геометрии
 называютсяпрямыми,
если различные блоки пересекаются не
более чем в одной точке. В этом случае
множество блоков называется множеством
прямых и мы будем пользоваться неформальным
языком, т.е. такими выражениями, как
“прямая проходит через точку”, “точка
лежит на прямой” и др.
называютсяпрямыми,
если различные блоки пересекаются не
более чем в одной точке. В этом случае
множество блоков называется множеством
прямых и мы будем пользоваться неформальным
языком, т.е. такими выражениями, как
“прямая проходит через точку”, “точка
лежит на прямой” и др.
Если
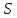 есть такая геометрия точек и прямых,
что каждая прямая имеет ровно
есть такая геометрия точек и прямых,
что каждая прямая имеет ровно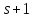 точку, каждая точка лежит ровно на
точку, каждая точка лежит ровно на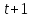 прямой
прямой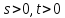 и
и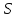 является сильно -однородной
является сильно -однородной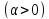 то тогда
то тогда называется
называется
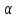 -
частичной геометрией порядка
-
частичной геометрией порядка
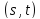 (для краткости
(для краткости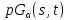 или даже
или даже ).
Связное расширение семейства частичных
геометрий
).
Связное расширение семейства частичных
геометрий обозначается как
обозначается как (или даже
(или даже ).
).
Можно
показать, что в
 - геометрии
- геометрии для любого антифлага
для любого антифлага ,
если
,
если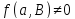 ,
то
,
то
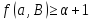 и
и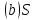 является треугольной геометрией тогда
и только тогда, когда она
является треугольной геометрией тогда
и только тогда, когда она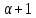 - однородна.
- однородна.
Если
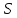 - частичная геометрия
- частичная геометрия ,
то двойственная геометрия
,
то двойственная геометрия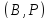 ,
в которой каждая точка отождествляется
с пучком проходящих через нее прямых,
является частичной геометрией
,
в которой каждая точка отождествляется
с пучком проходящих через нее прямых,
является частичной геометрией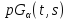 .
Обобщенный четырехугольник
.
Обобщенный четырехугольник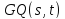 - это частичная геометрия
- это частичная геометрия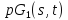 .
Геометрия
.
Геометрия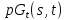 является сетью, а
является сетью, а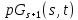 является 2-схемой с
является 2-схемой с .
Коклика из
.
Коклика из
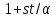 точек в точечном графе геометрии
точек в точечном графе геометрии называется овоидом.
называется овоидом.
В
данной работе мы исследуем
 – однородные геометрии
– однородные геометрии с
с и сильно
и сильно – однородные геометрии с
– однородные геометрии с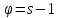 .
.
Пусть
геометрия
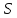 является
является – однородной
– однородной
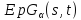 .
Если
.
Если
 то
то называется одноточечным расширением
(и граф
называется одноточечным расширением
(и граф является полным). Например, 3-схема Матье
с параметрами
является полным). Например, 3-схема Матье
с параметрами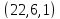 - это одноточечное расширение проективной
плоскости
- это одноточечное расширение проективной
плоскости .
.
Если
 ,
то геометрия
,
то геометрия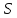 будет сильно (
будет сильно (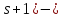 однородной, и
однородной, и является полным многодольным графом
является полным многодольным графом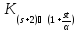 .
В этом случае для любой точки a множество
точек вычета
.
В этом случае для любой точки a множество
точек вычета имеет разбиение на
имеет разбиение на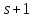 овоидов. Среди известных обобщенных
четырехугольников только
овоидов. Среди известных обобщенных
четырехугольников только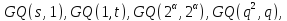
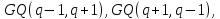 где
где – степень
простого числа, допускают разбиение
точечного множества на овоиды.
– степень
простого числа, допускают разбиение
точечного множества на овоиды.
Пример
1. Для любого
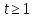 имеется единственная геометрия
имеется единственная геометрия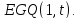 Ее точечный граф является полным
трехдольным графом
Ее точечный граф является полным
трехдольным графом ,
а множество блоков совпадает с множеством
3-клик этого графа.
,
а множество блоков совпадает с множеством
3-клик этого графа.
Пример
2. Сильно
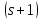 -
однородный расширенный четырехугольник
-
однородный расширенный четырехугольник существует
при всех
существует
при всех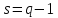 ,
где
,
где есть степень 2, а при
есть степень 2, а при и
и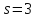 является единственным.
является единственным.
Пусть
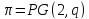 ,
, -
точка в
-
точка в
 ,
, - гиперовал, содержащий
- гиперовал, содержащий ,
а
,
а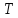 обозначает группу (порядка
обозначает группу (порядка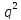 )
всех элаций с центром в точке
)
всех элаций с центром в точке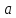 .
Точками
.
Точками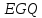 являются все точки
являются все точки ,
отличные от
,
отличные от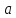 ;
блоками являются прямые, не содержащие
;
блоками являются прямые, не содержащие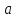 ,
и трансляции прямой
,
и трансляции прямой под
действием группы
под
действием группы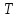 .
.
Примеры
 -однородных
-однородных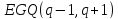 для
для построены
построены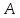 .
Пасини и Д. Пасечником.
.
Пасини и Д. Пасечником.
Теорема
1. Пусть
S
является s-однородной
геометрией
 а
а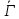 -дополнение
к
-дополнение
к .
Тогда либо
.
Тогда либо (и геометрия
(и геометрия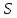 известна), либо
известна), либо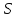 есть
есть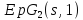 ,
,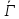 -
является сильно регулярным графом с
-
является сильно регулярным графом с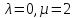 ,
и
,
и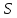 есть геометрия вершин и клик графа
есть геометрия вершин и клик графа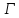 ,
соответствующих
,
соответствующих для
для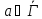 ;
либо
;
либо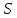 сильно
сильно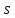 -однородна
и одно из следующих утверждений верно:
-однородна
и одно из следующих утверждений верно:
(1)
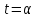 ,
и
,
и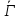 есть граф, являющийся квадратной решеткой
на
есть граф, являющийся квадратной решеткой
на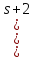 вершинах;
вершинах;
(2)
 ,
, ,
, делит
делит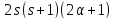 ,
и
,
и есть треугольный граф на (
есть треугольный граф на ( вершинах.
вершинах.
Пример
3. Сильно -однородная геометрия
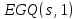 существует для всех
существует для всех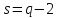 ,
где
,
где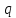 есть степень двойки.
есть степень двойки.
Пусть
 ,
,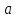 и
и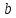 являются точками
являются точками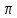 ,
, есть прямая
есть прямая ,
, -гиперовал,
содержащий
-гиперовал,
содержащий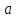 и
и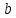 ,
а
,
а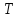 -
это группа всех центральных коллинеаций
с центром
-
это группа всех центральных коллинеаций
с центром
 и осью, содержащей
и осью, содержащей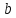 .
Тогда
.
Тогда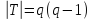 ,
,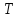 фиксирует
все прямые, проходящие через
фиксирует
все прямые, проходящие через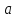 ,
и является точно 2-транзитивной группой
на множестве прямых, проходящих через
,
и является точно 2-транзитивной группой
на множестве прямых, проходящих через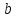 и отличных от
и отличных от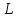 .
.
Множество
точек геометрии
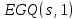 состоит из точек
состоит из точек ,
которые не лежат наL,
а множество блоков является объединением
множества прямых
,
которые не лежат наL,
а множество блоков является объединением
множества прямых
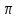 ,
не содержащих
,
не содержащих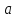 или
или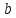 ,
и образов
,
и образов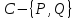 под действием группы элаций
под действием группы элаций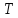 .
.
Пример
4. Сильно 3-однородная геометрия
 существует.
существует.
Пусть
точечное множество
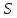 есть множество позиций
есть множество позиций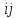 квадратной матрицы порядка 5, а множество
блоков
квадратной матрицы порядка 5, а множество
блоков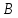 задано наборами
задано наборами ,
такими, что
,
такими, что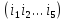 - перестановка.
- перестановка.
Ясно,
что
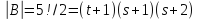 для
для и
и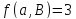 для любого антифлага
для любого антифлага .
.
Далее,
для точки
 имеем
имеем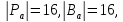 каждая точка из
каждая точка из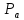 принадлежит трем блокам из
принадлежит трем блокам из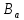 и каждый блок из
и каждый блок из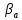 содержит 4 точки из
содержит 4 точки из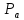 .
Таким образом,
.
Таким образом,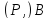 является сильно 3-однородной геометрией
является сильно 3-однородной геометрией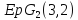 .
.
Теорема
2. Пусть
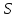 является сильно
является сильно -однородной
геометрией
-однородной
геометрией .
Тогда либо
.
Тогда либо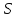 является геометрией
является геометрией для некоторого нечетного
для некоторого нечетного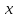 ,
либо
,
либо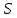 равняется
равняется или
или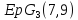 .
.
Дж.
Тас построил частичную геометрию
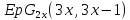 с
с
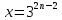 с помощью спреда гиперболической
квадрики в проективном пространстве
с помощью спреда гиперболической
квадрики в проективном пространстве .
К настоящему времени известно существование
такого спреда только для случая
.
К настоящему времени известно существование
такого спреда только для случая .
.
Теоремы 1 и 2 обобщают соответствующие результаты П. Камерона и Дж. Фишера по расширениям обобщенных четырехугольников на случай частичных геометрий.
