зависит от одного параметра a, и является простейшим одномерным отображением, проявляющим сингулярность. Отображения с одной критической точкой называются унимодальными.

Унимодальное отображение - гладкое отображение на себя при условии, что оно имеет единственную критическую точку (ноль производной).

Все унимодальные отображения демонстрируют похожее динамическое поведение. Основных типов динамических режимов два: 1) стационарные или периодические режимы, 2) хаотические режимы. В первом случае итерации в конечном итоге посещают только конечный набор разных значений, всегда повторяющиеся в фиксированном порядке. В случае (2) состояние системы никогда не повторяется точно и, по-видимому, эволюционирует неупорядоченным образом.

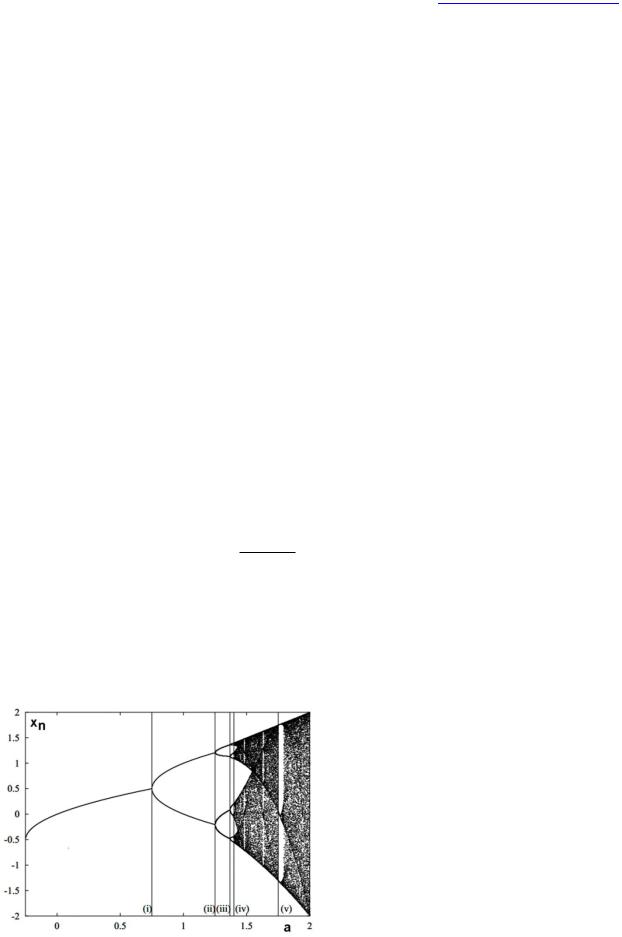
Бифуркационная диаграмма ограничена диапазоном a0<a<aR. Между a0=-1/4 и a1 =3/4 предельный набор состоит из одного значения. Это соответствует стационарному режиму, который есть периодическая орбита периода-1. При a=a1 происходит бифуркация, рождающая периодическую орбиту периода-2: итерации колеблются между двумя значениями – бифуркация удвоения периода. При a=a2=5/4 существует еще одна бифуркация удвоения периода, где орбита периода-2 уступает место орбите периода-4.

Бифуркации удвоения периода, возникающие при a=a1 и a=a2, являются первыми двумя членами бесконечной серии – каскада удвоения периода, в котором для каждого целого n создается орбита периода 2n. Бифуркация при a=a3, приводящая к орбите периода-8, легко видна на бифуркационной диаграмме на рис. 13, та, что при a=a4 едва заметна, а следующие совершенно неразличимы для невооруженного глаза. Это связано с тем, что значения параметра a, при которых создается орбита периода 2n, геометрически сходятся к точке накопления a∞=1.401155189... с коэффициентом сходимости,

существенно превышающим 1: lim an an 1 4,6692016091...

n an 1 an

Постоянная δ, обладает замечательным свойством: периоды удвоения каскадов, наблюдаемые в чрезвычайно большом классе систем, имеют скорость сходимости, определяемую δ. В точке накопления a∞ период решения становится бесконечным. На рис. 13 справа от этой точки система переходит в хаотические режимы, что видно по обилию тёмных областей в этой части бифуркационной диаграммы, которые указывают на то, что система посещает много разных состояний. Каскад удвоения периода - один из наиболее известных путей хаоса и может наблюдаться во многих низкоразмерных системах.

Рис. 13: Бифуркационная диаграмма отображения (4): рассчитана для нескольких значений параметров от a=- 0.25 до a=2.0; проведено 50

последовательных итераций отображения с целью вымираня переходных процессов. Вертикальные линии отмечают создание (i) орбиты периода-2; (ii) орбиты периода-4; (iii) орбиты периода-8 и (iv) точка накопления каскада удвоения периода; (v) начальная точка окна периода-3.

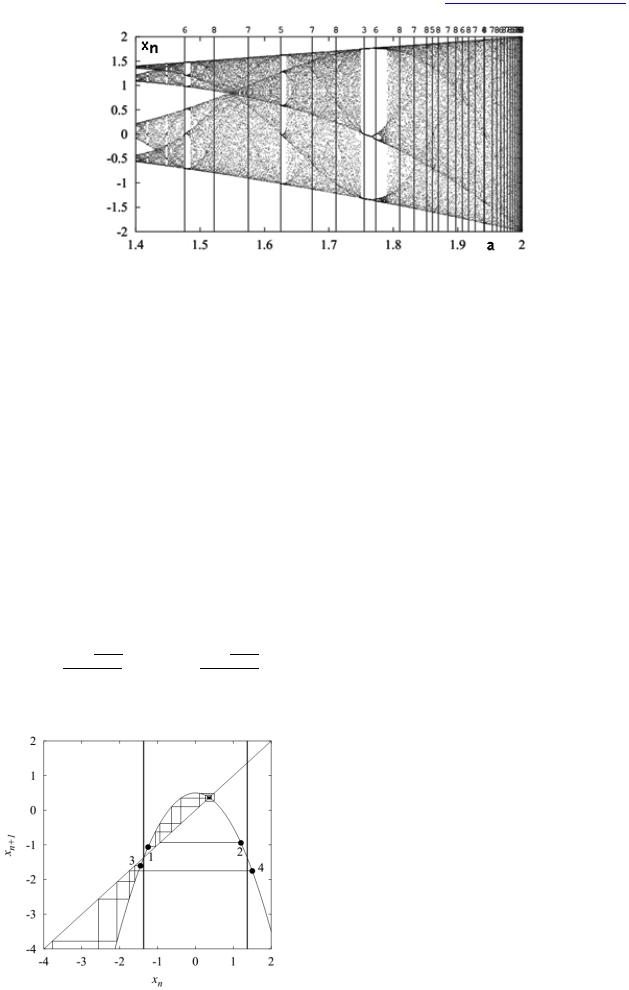
http://profbeckman.narod.ru/

Рис. 14: Увеличенный вид хаотической зоны бифуркационной диаграммы рис. 13.

Внутри периодических окон периода до 8 вертикальные линии указывают значения параметров, где соответствующие орбиты наиболее стабильны (период указан над линией).

В хаотической области есть относительно большое периодическое окно, соответствующее области устойчивости орбиты периода-3, которое начинается с а=7/4, внутри хаотической зоны. Периодические окна и хаотические области произвольно часто чередуются; между любыми двумя периодическими окнами бесконечно много периодических окон. Периодические окна видны невооруженным глазом только у очень низких периодов. У более высоких периодов (1) периодическое окно слишком узкое по сравнению с масштабом графика, и (2) количество выборок достаточно велико, чтобы окно не могло отличаться от хаотических режимов.

Конечно, было бы полезно определить для каждого периодического решения диапазон значений параметров, по которым он устойчив. Увы! Эта задача недостижима, но всё же простые топологические методы позволяют классифицировать разные периодические режимы и ответить на такие вопросы, как продолжается ли последовательность различных динамических режимов, возникающих при увеличении параметра a, возможно диагностика сложности хаоса и др.

Поиск неподвижных точек просто сводится к решению квадратичного уравнения x=a-x2 (5)

который имеет два решения:

Эти выражения 2.4 имеют смысл только при a>a0=-1/4. Ниже этого значения все орбиты уходят в бесконечность. Бесконечно удаленную точку x∞, можно формально рассматривать как другую неподвижную точку

системы, хотя и нефизическую.

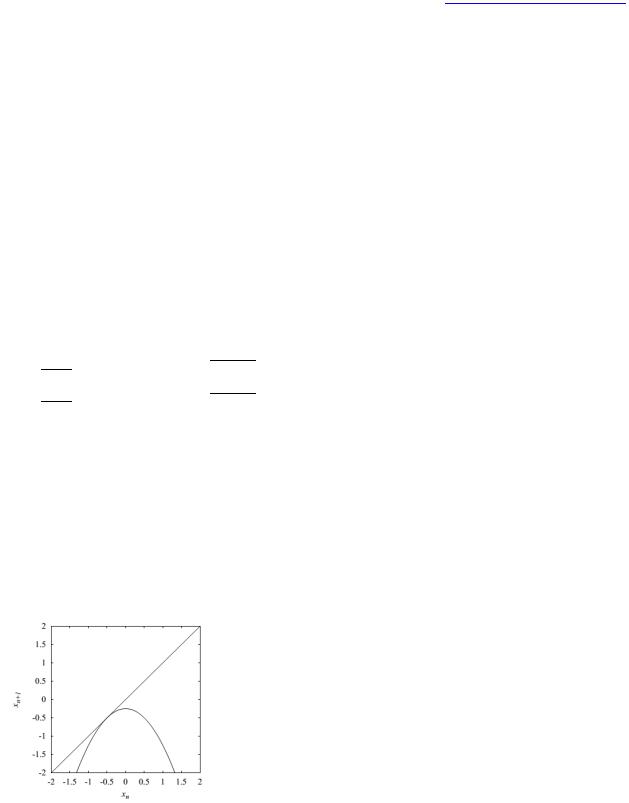
Рис. 14: Бассейн притяжения неподвижной точки x+ расположен между левой неподвижной точкой x- и ее прообразом, обозначенной двумя вертикальными линиями.

Орбиты, помеченные 1 и 2, находятся внутри бассейна и сходятся к х+. Орбиты, помеченные 3 и 4, находятся за пределами бассейна и уходят в бесконечность (т. е. сходятся к бесконечной точке x∞).

Важным качественным изменением, происходящим при a=a0, является повсеместное явление низкоразмерной нелинейной динамики,

http://profbeckman.narod.ru/

Орбита периода 2 (x1, x2) появляется при a=a1=3/4 и существует для каждого a>a1. Используя правило цепочки для производных, получим множитель фиксированной точки x1 функции f2 как

же множитель, который определяется как множитель орбиты (x1, x2). В точке бифуркации a=a1 имеем μ1,2=1, сигнатура двух периодических точек x1 и x2 вырождается при бифуркации удвоения периода. Однако структура этой бифуркации не полностью аналогична структуре касательной бифуркации, рассмотренной ранее. Действительно, две периодические точки x1 и x2 также вырождены с неподвижной точкой x+. Таким образом, бифуркация удвоения периода фиксированной точки x+ является ситуацией, когда вторая итерация f2 имеет три вырожденные неподвижные точки. Сигнатура этого тройного вырождения соответствует особой форме более высокого порядка чем сингулярность складчатости, упомянутой при обсуждении касательной бифуркации. Заметим, что x+ имеет мультипликатор -1 как фиксированную точку f при бифуркации и, следовательно, существует по обе стороны от бифуркации: он просто становится неустойчивым при a=a1. Напротив, x1 и x2 имеют мультипликатор 1 для первых итераций f, при которых они являются неподвижными точками, и, следовательно, существуют только с одной стороны бифуркации. Орбита периода-2 устойчива только в конечном диапазоне параметров. Другой конец области устойчивости имеет вид a=a2=5/4, где μ1,2=-1. При этом значении параметра происходит новая бифуркация удвоения периода, где орбита периода-2 теряет устойчивость и рождает орбиту периода-4. Как показано на рис. 13, удвоение периода происходит неоднократно, пока не будет создана орбита бесконечного периода.

20.3 Подобие окон периодической динамики

Общая особенность для хаотических динамических систем состоит в том, что при изменения параметров рождается устойчивая и неустойчивая орбиты с периодом n (касательная бифуркация). Далее происходит переход к хаосу через каскад удвоения периода. Все заканчивается кризисом, при котором неустойчивая орбита с периодом n рожденная в исходной касательной бифуркации сталкивается с хаотическим аттрактором. Область параметров между касательной бифуркацией и кризисом называется окном периодической динамики с периодом n. Заметим, что в этом случае центральная часть рисунка подобна всей бифуркационной диаграмме (рис. 16).

Так, при С=-1.75 в окне с периодом 3 в результате тангенциальной бифуркации отображения f o3 возникают устойчивая и неустойчивая орбиты с периодом 3 (в верхней части окна). Устойчивая орбита с периодом 3 показана ниже налево. Если задать N=3 (рис. 17б), то мы получим 8 пересечений (неподвижных точек отображения f o3). Два из них – неустойчивые неподвижные точки. Остальные шесть пересечений принадлежат устойчивой и неустойчивой орбитам с периодом 3.

На рис. 17а периодическая орбита проходит через два "линейных" (по краям) и один квадратичный участок параболы (в центре). Поэтому в окрестности x=0 отображение f o3 с точностью до растяжений совпадет с квадратичным (это преобразование называется