http://profbeckman.narod.ru/

Рассмотрим методы изучения устойчивости нулевого решения линейной однородной системы с постоянными коэффициентами y Ay . Эта методика тесно связана с расположением на комплексной плоскости корней характеристического многочлена Pn( )=det|A- E| Нулевое решение асимптотически устойчиво, если все корни лежат строго в левой полуплоскости (матрица А устойчивая). Нулевое решение не устойчиво, если есть корень, лежащий в правой полупоскости. Если характеристический многочлен имеет чисто мнимые корни, то асимптотический устойчивости нет.

Для систем уравнений есть одна тонкость: если характеристический многочлен имеет кратные чисто мнимые корни, то нельзя сразу сделать вывод о неустойчивости нулевого решения (в отличие от уравнения). Может случиться, что и в случае кратных корней фундаментальная матрица состоит только из ограниченных функций, и нулевое решение будет устойчивым. Это произойдёт, если алгебраическая кратность соответствующего корня совпадёт с его геометрической кратностью. В противном случае возникнут неограниченные решения, и нулевое решение будет неустойчивым. Может оказаться, что незначительное изменение начального условия оказывает незначительное краткосрочное влияние на решение, однако при больших временах различия между этими двумя решениями могут стать драматическими. Чувствительная зависимость решений от начальных условий способна проявляться уже в весьма простых линейных уравнениях. Более того, непрерывная зависимость не мешает решениям проявлять хаотическое поведение.

14.5 Метод функций Ляпунова

Второй метод Ляпунова – совокупность приемов и средств исследования устойчивости решений систем дифференциальных уравнений при помощи специальных функций Ляпунова.

А.М. Ляпунов установил ряд общих достаточных условий устойчивости и неустойчивости невозмущенного движения, описываемого системой ОДУ. Сводя вопрос устойчивости невозмущенного движения к вопросу устойчивости положения равновесия, Ляпунов связал факт устойчивости или неустойчивости с наличием функции V(x1,...,xn), производная которой взятая согласно системе дифференциальных уравнений, обладает определёнными свойствами.

С помощью функций Ляпунова можно оценить область притяжения, т.е. многообразие всех начальных возмущений, исчезающих во времени, можно оценить влияние постоянно действующих возмущений. Зная функции Ляпунова можно решать задачи устойчивости "в большом", т.е. оценивать область начальных возмущений, не выходящих с течением времени за пределы заданной заранее области. В некоторых случаях вид функции Ляпунова позволяет также решить вопрос о наличии периодического решения.

Исследование устойчивости по первому приближению Ляпунова является простым и эффективным методом, который, однако, работает только в случае, когда точка покоя является невырожденной (определитель матрицы не равен нулю) и не является центром. В сложных ситуациях более эффективным оказывается второй метод Ляпунова, основанный на построении функции Ляпунова, позволяющих получить достаточные условия в большом. Этот метод основан на формировании и рассмотрении специальных функций V(x,y), где х и у – небольшие отклонения (вариации) переменных от состояния равновесия, соответствующего х=0 и у=0.

Функция Ляпунова – скалярная функция, заданная на фазовом пространстве системы, с помощью которой можно доказать устойчивость положения равновесия. Метод функций Ляпунова применяется для исследования устойчивости различных дифференциальных уравнений и систем.

http://profbeckman.narod.ru/

Сначала рассмотрим функцию Ляпунова V(х) для автономной системы первого

функция Ляпунова должна быть постоянной на равновесном решении.)

Непрерывно дифференцируемой функции Ляпунова не возрастает тогда и только тогда, когда её производная неотрицательна и строго убывает, если её производная строго меньше 0. Вычислив производную V(x(t)), установим основные критерии для функций Ляпунова.

Критерий устойчивости и неустойчивости равновесий системы, обладающей функцией Ляпунова, определяется теоремой.

Теорема. Пусть V(x) – функция Ляпунова для автономной системы x F(x) . Если x0

–строгий локальный минимум V, то x0 – устойчивая точка равновесия. Если V(x) – строгая функция Ляпунова, то x0 – асимптотически устойчивое равновесие. С другой стороны, любая критическая точка строгой функции Ляпунова V(x), которая не является локальным минимумом, является неустойчивой точкой равновесия.

Локальные максимумы строгих функций Ляпунова являются нестабильными равновесиями. Если функция Ляпунова не возрастает, то любое решение, которое начинается достаточно близко к минимальному значению, не может уйти далеко, т.е. система устойчива. (Если вы топчитесь на дне долины и в гору высоко не поднимаетесь, то на дне и останетесь). В строгом случае функция Ляпунова убывает на неравновесных решениях, поэтому она должна перейти к минимальному значению V при t→∞. (Если, гуляя по ущелью постоянно терять высоту, то, в конце концов, достигнешь дна). Если же неравновесное решение начинается вблизи точки равновесия, не являющейся локальным минимумом, то неуклонное уменьшение функции Ляпунова, означает, что решение все дальше и дальше отходит от равновесия, демонстрируя нестабильность.

Перейдём теперь к двумерной функции V(x,y). Она должна обладать следующими свойствами:

–в некоторой области, окружающей начало координат, V(x,y) непрерывна вместе со всеми частными производными первого порядка;

–в начале координат V(0,0)=0;

–во всех остальных точках этой области V(x,y) отличается от нуля и принимает значение одного знака.

Более строго функция Ляпунова определяется следующим образом.

Непрерывно дифференцируемая функция V ( y) называется функцией Ляпунова для

окрестности начала координат обладает функцией Ляпунова, то начало координат является устойчивым положением равновесия. Если же выполняется более сильное

http://profbeckman.narod.ru/

Рис. 11. График функции V=x2+y2.

Функция V(x,y), обладающая такими свойствами, называется знакопеременной: определённо-положительной или определённо отрицательной. Функцию называют знакопостоянной (положительной или отрицательной), если она также сохраняет в области постоянства знака, однако нулевые значения имеет не только в начале координат. Эти функции называют функциями Ляпунова.

Рассмотрим некоторые функции V(x,y). Функция

построенная на рис. 11а является знакопеременной (определённо-положительной): в точке равновесия V(0;0), а в любых других точках V>0. Функция V=x2-2xy+y2=(x-y)2, построенная на рис. 11б, знакопостоянна (положительная), но не знакоопределенна, так как V=0 не только в начале координат, но и в точках, где х=у; при иных значениях х и у V>0.

Обращаясь к знакопеременным функциям, например, к Ур.18, можно заметить, что кривые V(x,y)=С, где С - фиксированный параметр, являются замкнутыми кривыми, охватывающими начало, координат, причем кривые с меньшим С располагаются ближе к началу координат. Используя эту особенность V-функций, Ляпунов доказал теоремы.

Теорема 1. Если дифференциальные уравнения возмущенного движения таковы, что можно найти знакоопределяющую функцию V(x,y), производная которой dV/dx знакопостоянная функцияй противоположного с V знака или тождественно равна нулю, то равновесие системы в начале координат устойчиво в смысле Ляпунова (невозмущенное движение устойчиво).

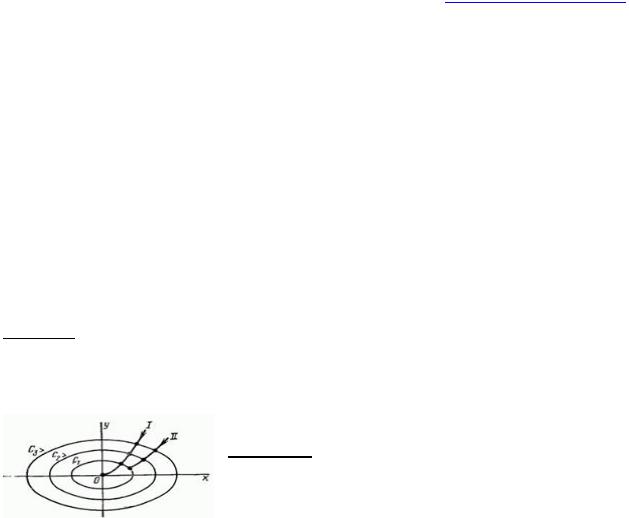
Рис. 12. К теореме 2.

Теорема 2. Если для системы дифференциальных уравнений x F(x), существует знакоопределенная

функция V, полная производная которой по времени dV/dt также знакоопределена (знак противоположен V), то равновесие системы в начале координат

асимптотически устойчиво.

Для иллюстрации этих теорем на рис. 12 построено несколько замкнутых кривых определённо положительной функции V(x,y)=C для значений C1<C2<C3. Аргументами функции V(x,y) являются отклонения х и у от состояния равновесия, которые изменяются во времени в соответствии с характером возмущённого движения. Поэтому и значения функции V[x(t),y(t)] и её производной dV/dt также изменяются во времени.

Пусть производная dV/dt знакоопределенна и имеет противоположный с V знак, для рис.12 она определенно-отрицательна (dV/dt<0). Если в начальный момент t0 V-функция имела значение V0=С3, то за время t-t0 она изменится на величину

Очевидно, V<V0=C3. В рассматриваемых условиях с течением времени функция V последовательно проходит через значения С3, С2, С1 и вместе со своими компонентами х и у приближается к началу координат (линия t на рис. 12), что означает асимптотическую устойчивость состояния равновесия.

Если же функция dV/dt в рассматриваемом случае знакопостоянна (отрицательна), то в процессе уменьшения V, происходящем согласно (19), она может достичь значения V=V1, при котором dV/dt=0 при х10. Тогда дальнейшее уменьшение V функции, т.е. приближение к состоянию равновесия приостановится. Этому соответствует неасимпотическая устойчивость состояние равновесия и линии II на рис. 12.

Уяснить смысл функций Ляпунова и сформулированных в приведенных выше теоремах условий устойчивости легко с помощью понятий фазового пространства. Если V(x,y) – знакоопределенная функция, то уравнение V(x,y)=C обычно определяет в фазовом