Вариационное исчисление

Рассмотрим данную задачу оптимального управления как задачу Лагранжа вариационного исчисления. Для нахождения необходимых условий экстремума применим теорему Эйлера-Лагранжа. Функция Лагранжа имеет вид: , где  — граничные условия. Лагранжиан имеет вид: , где , ,  — n-мерные вектора множителей Лагранжа.

Необходимые условия экстремума, согласно этой теореме, имеют вид:

• стационарность по u: 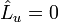, (3)

• стационарность по x, уравнение Эйлера: (4)

• трансверсальность по x: , 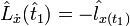(5)

Необходимые условия (3-5) составляют основу для определения оптимальных траекторий. Написав эти уравнения, получаем двухточечную граничную задачу, где часть граничных условий задана в начальный момент времени, а остальная часть — в конечный момент.

Принцип максимума Понтрягина

Необходимость в принципе максимума Понтрягина возникает в случае, когда нигде в допустимом диапазоне управляющей переменной невозможно удовлетворить необходимому условию (3), а именно .

В этом случае условие (3) заменяется на условие (6):

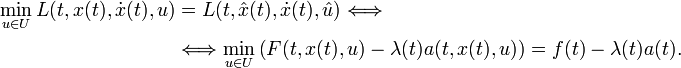
В этом случае согласно принципу максимума Понтрягина величина оптимального управления равна величине управления на одном из концов допустимого диапазона. Уравнения Понтрягина записываются при помощи функции Гамильтона Н, определяемой соотношением .

Из уравнений следует, что функция Гамильтона H связана с функцией Лагранжа L следующим образом: .

Подставляя L из последнего уравнения в уравнения (3-5) получаем необходимые условия, выраженные через функцию Гамильтона:

• уравнение управления по u: 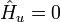, (7)

• уравнение состояния: 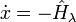, (8)

• сопряжённое уравнение: 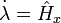, (9)

• трансверсальность по x: 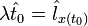, 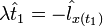(10)

Необходимые условия, записанные в такой форме, называются уравнениями Понтрягина.

Где применяется

Принцип максимума особенно важен в системах управления с максимальным быстродействием и минимальным расходом энергии, где применяются управления релейного типа, принимающие крайние, а не промежуточные значения на допустимом интервале управления.

Метод динамического программирования

Метод динамического программирования основан на принципе оптимальности Беллмана, который формулируется следующим образом: оптимальная стратегия управления обладает тем свойством, что каково бы ни было начальное состояние и управление в начале процесса последующие управления должны составлять оптимальную стратегию управления относительно состояния, полученного после начальной стадии процесса.

http://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5#.D0.97.D0.B0.D0.B4.D0.B0.D1.87.D0.B0_.D0.BE.D0.BF.D1.82.D0.B8.D0.BC.D0.B0.D0.BB.D1.8C.D0.BD.D0.BE.D0.B3.D0.BE_.D1.83.D0.BF.D1.80.D0.B0.D0.B2.D0.BB.D0.B5.D0.BD.D0.B8.D1.8F-Оптимальное управление.

Математические основы оптимизации управления динамическими системами.

Уравнение Эйлера

Определение . Пусть М – некоторое пространство функций.

Отображение J: М → \1 называется функционалом.

Ниже будем рассматривать следующие пространства функций:

C[t1, t2] – непрерывные на отрезке [t1, t2] функции, с нормой, определенной следующим образом: ||x(⋅)||0 = max{ |x(t)|, t∈[t1, t2]}; C1[t1, t2] – непрерывно дифференцируемые на отрезке [t1, t2] функции, снормой ||x(⋅)||1 = max{ ||x(⋅)||0, ||x'(⋅)||0}. Простейшая задача вариационного исчисления формулируетсяследующим образом: найти экстремум функционала видаJ(x(⋅)) = F t x x dttt∫21( , , ') (1.1) на множестве кусочно-гладких функций x(⋅), соединяющих точки (t1, x1) и(t2, x2), т.е. удовлетворяющих краевым условиям x(t1) = x1; x(t2) = x2. Функции x(⋅), удовлетворяющие ограничениям задачи (в данном случае граничным условиям), называются допустимыми. Определение . Говорят, что x*(⋅) доставляет слабый локальныймаксимум функционалу J, если ∃ ε > 0: для любой допустимой кривой x(⋅), такой, что || x*(⋅) – x(⋅)||1 < ε, выполнено: J(x(⋅)) ≤ J(x*(⋅)). Говорят, что x*(⋅) доставляет сильный локальный максимум функционалуJ, если ∃ ε > 0: для любой допустимой кривой x(⋅), такой, что || x*(⋅) – x(⋅)||0< ε, выполнено J(x(⋅)) ≤ J(x*(⋅)). Необходимое условие слабого экстремума функционала (1.1) даетсяуравнением Эйлера: Fx – Fx 'dtd = 0. (1.2) Гладкое решение уравнения Эйлера называется экстремалью функционала J. Сотсков А.И., Колесник Г.В. Управление динамическими системами в задачах экономики:

Примеры:

Найти экстремаль в задаче: J = t x tx dt ∫+212 2( ' ' ) ; x(1) = a; x(2) = b.

Решение :

F(t, x, x') = t2x' + tx'2 , Fx = 0, Fx' = t2 + 2tx'. Составимуравнение Эйлера: Fx – Fx 'dtd = 2t + 2x' + 2 tx'' = 0. Видно, что в это уравнение не входит х. Обозначим у = x', тогда y' = x'' иуравнение примет видt + у + tу' = 0. Решением данного уравнения является у(t) = c/t – t/2. Тогдаx(t) = y t dt ∫( ) + d = c ln t – t2/4 + d. (1.3) Находя постоянные с и d из краевых условий, окончательно получаемx*(t) =ln2b− a+3/4ln t – t2/4 + a + 1/4. Функция x*(t) гладкая на [1, 2], следовательно, она является экстремалью. Замечание . В задаче с функционалом J = t x tx dt ∫+102 2( ' ' )экстремалиотсутствуют, так как решения уравнения Эйлера теряют гладкость наотрезке [0, 1].

http://crysalis.chat.ru/sample.pdf-Математические основы оптимизации

управления динамическими системами.

Многокритериальная оптимизация или программирование  — это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

Задача многокритериальной оптимизации встречаются во многих областях науки, техники и экономики.