
- •Глава 1. Волновые свойства частиц
- •§1.1. Корпускулярно-волновой дуализм
- •§1.2. Волны де Бройля и их экспериментальное подтверждение
- •§1.3. Статистическое толкование волн де Бройля и соотношение неопределенностей
- •Глава 2. Математический аппарат квантовой механики
- •§ 2.1. Уравнение Шредингера
- •§2.2. Операторы
- •§2.3. Самосопряженные (эрмитовы) операторы и их свойства
- •§2.4. Вычисление средних значений. Обозначения Дирака
- •§2.5. Дифференцирование операторов по времени
- •Глава 3. Уравнение Шредингера в одном измерении
- •§3.1. Одномерная потенциальная яма с бесконечно высокими стенками
- •§3.2. Одномерная потенциальная яма с конечными стенками
- •§3.3. Потенциальные барьеры
- •§3.4. Линейный гармонический осциллятор
- •§3.5. Решение уравнения Шредингера одномерного осциллятора при помощи операторов рождения и уничтожения
- •Глава 4. Момент импульса
- •§4.1. Момент импульса в квантовой механике
- •§4.2. Оператор момента импульса в сферической системе координат
- •§4.3. Оператор квадрата момента импульса в сферической системе координат
- •Глава 5. Физика атомов
- •§5.1. Уравнение Шредингера в центральном поле
- •§5.2. Уравнение для радиальной части волновой функции
- •§5.3. Уравнение для угловой части
- •§5.4. Состояние электронов в атоме. Спин электрона
- •§5.5. Магнитный момент атома
- •Глава 6. Теория возмущений
- •§6.1. Стационарная теория возмущений
- •§6.2. Нестационарная теория возмущений
- •§6.3. “Золотое ” правило Ферми
- •Глава 1. Введение 4
Глава 5. Физика атомов
§5.1. Уравнение Шредингера в центральном поле
В
центральном поле потенциальная энергия
зависит только от модуля разности
координат
взаимодействующих частиц. Известно,
что задача о движении двух взаимодействующих
тел сводится к решению задачи о движении
одной частицы с эффективной массой
в поле центральных сил. Если масса одного
тела значительно больше массы другого
M
>>
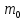 , то можно рассматривать движение частицы
массы
=
, то можно рассматривать движение частицы
массы
=
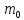 в полеU(r),
где r
ее расстояние от второй частицы. Для
атома водорода, которым мы интересуемся
в первую очередь,
в полеU(r),
где r
ее расстояние от второй частицы. Для
атома водорода, которым мы интересуемся
в первую очередь,
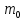 – это масса свободного электрона.
– это масса свободного электрона.
Рассмотрим стационарное уравнение Шредингера в центральном поле:

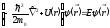 (5.1)
(5.1)
В сферической системе координат оператор Лапласа имеет вид
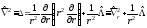 ,
(5.2)
,
(5.2)
где угловая часть оператора Лапласа, называемая иногда оператором Лежандра, равна
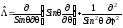 .
(5.3)
.
(5.3)
Сравнивая
(5.3) с (4.14), замечаем, что
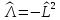 .
.
Оператор
Лежандра
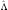 не зависит от радиусаr
и конкретного вида потенциала U(r),
что позволяет разделить уравнение
Шредингера на две части, одна из которых
зависит только от радиуса, а другая от
угловых переменных. Для этого подставим
в уравнение Шредингера (5.1) волновую
функцию вида
не зависит от радиусаr
и конкретного вида потенциала U(r),
что позволяет разделить уравнение
Шредингера на две части, одна из которых
зависит только от радиуса, а другая от
угловых переменных. Для этого подставим
в уравнение Шредингера (5.1) волновую
функцию вида
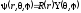 .
(5.4)
.
(5.4)
Перепишем (5.1) в более удобном виде
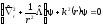 ,
(5.5)
,
(5.5)
где параметр
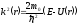 (5.6)
(5.6)
зависит
только от радиуса r.
Умножив уравнение (5.5) на
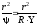 и, сокращая соответствующие части
волновой функции, получим
и, сокращая соответствующие части
волновой функции, получим
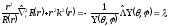 (5.7)
(5.7)
Левая
и правая части этого уравнения зависят
от разных переменных. Их равенство
возможно только тогда, когда они равны
константе, которую называют постоянной
разделения .
Учитывая, что
 , получаем, заменяя большие буквы
маленькими, что
, получаем, заменяя большие буквы
маленькими, что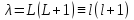 .
.
§5.2. Уравнение для радиальной части волновой функции
Введя постоянную , запишем уравнение для радиальной части
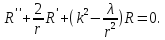 (5.8)
(5.8)
Это
уравнение зависит от потенциала U(r).
Поэтому, чтобы решать данное уравнение
необходимо знать конкретный вид
центрального потенциала. Для атома
водорода
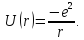 Естественная
система единиц включает в себя
фундаментальные постоянные
Естественная
система единиц включает в себя
фундаментальные постоянные
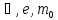 .
.
Введем атомную систему единиц, где:
единицей длины является
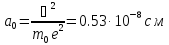 (боровский радиус),
(боровский радиус),единицей энергии -
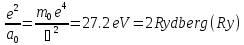 ,
,скорости
 где
где - постоянная тонкой структуры.
- постоянная тонкой структуры.
Чтобы перейти к этой системе единиц надо во всех формулах положить
 .
.
Тогда
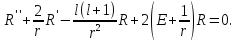 (5.9)
(5.9)
Это уравнение можно также записывать в виде
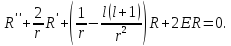
Величина,
заключенная в скобки, называется
эффективным
потенциалом
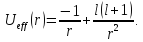 Благодаря второму слагаемому возникает
центробежный барьер, не позволяющий
электрону “упасть” на ядро.После
замены
Благодаря второму слагаемому возникает
центробежный барьер, не позволяющий
электрону “упасть” на ядро.После
замены
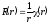 ,
получаем для радиальной функции
уравнение, не содержащее первой
производной:
,
получаем для радиальной функции
уравнение, не содержащее первой
производной:
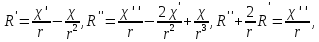
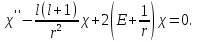 (5.10)
(5.10)
Будем решать уравнение Шредингера для случая, когда энергия собственных состояний отрицательна (E<0) и введем параметр
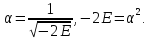
Тогда
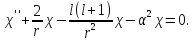 (5.11)
(5.11)
Найдем
асимптотику функции
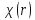 при
при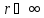 .
Для этого в (5.11) следует пренебречь
вторым и третьим членами уравнения, в
результате чего получаем уравнение
.
Для этого в (5.11) следует пренебречь
вторым и третьим членами уравнения, в
результате чего получаем уравнение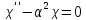 ,решением
которого будет функция
,решением
которого будет функция
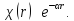
В
пределе
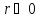 надо рассмотреть
надо рассмотреть Этому уравнению удовлетворяет функция
Этому уравнению удовлетворяет функция .
Из условия
.
Из условия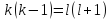 следует, что
следует, что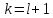 или
или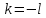 .
При отрицательном значенииk
.
При отрицательном значенииk
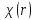 в нуле стремится к бесконечности, поэтому
в нуле стремится к бесконечности, поэтому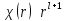 ,
а
,
а Для функции
Для функции имеем
имеем
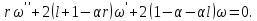 (5.12)
(5.12)
Решение ищем в виде ряда
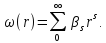 (5.13)
(5.13)
После
подстановки этого ряда в (5.12)
 получаем рекуррентное соотношение
получаем рекуррентное соотношение
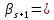 2
2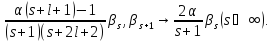 (5.14)
(5.14)
Таким
образом,
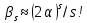 и, если ряд не оборвать, он сходится к
функции
и, если ряд не оборвать, он сходится к
функции .
В этом случае функция
.
В этом случае функция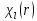 также стремится к бесконечности, хотя
из физических соображений она должна
стремиться к нулю. Чтобы обеспечить
правильное поведение волновой функции
в этом пределе ряд (5.14) надо оборвать на
некоторомs
= nr.
Тогда
также стремится к бесконечности, хотя
из физических соображений она должна
стремиться к нулю. Чтобы обеспечить
правильное поведение волновой функции
в этом пределе ряд (5.14) надо оборвать на
некоторомs
= nr.
Тогда
 (5.15)
(5.15)
Полином
 при подходящем выборе
при подходящем выборе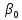 называется полиномом
Лагерра -
называется полиномом
Лагерра -
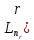 ).
Собственные значения энергии в атоме
водорода определяются соотношением
).
Собственные значения энергии в атоме
водорода определяются соотношением
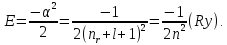 (5.16)
(5.16)
В
последней формуле мы ввели новое целое
квантовое число
 которое может принимать целые положительные
значения
которое может принимать целые положительные
значения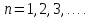 Это число, от которого зависят уровни
энергии, получило названиеглавного
квантового числа. Окончательное решение
радиального уравнения Шредингера для
атома водорода имеет вид:
Это число, от которого зависят уровни
энергии, получило названиеглавного
квантового числа. Окончательное решение
радиального уравнения Шредингера для
атома водорода имеет вид:
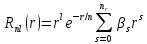 ,
(5.17)
,
(5.17)
где
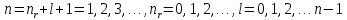 .
.
Рассмотрим
состояния с
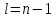 ,
для которых
,
для которых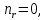 а
а – константа, которую можно легко найти
из условия нормировки
– константа, которую можно легко найти
из условия нормировки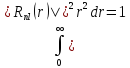 ,
,
используя
известный интеграл
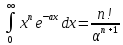 .
Таким образом, получим
.
Таким образом, получим
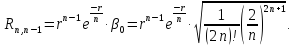
В
этих состояниях
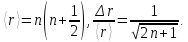 В основном состоянии (n=1)
В основном состоянии (n=1)
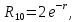
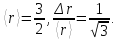 Зная
Зная ,
из (5.14) можно найти все остальные
,
из (5.14) можно найти все остальные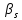 и
и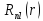 .
Для значенийn
= 1, 2 и 3 радиальные функции атома водорода
имеют вид:
.
Для значенийn
= 1, 2 и 3 радиальные функции атома водорода
имеют вид:
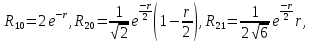
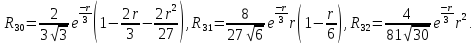
Энергии стационарных состояний водородоподобного атома определяются только главным квантовым числом n (для водорода Z=1)
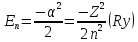 .
.
В
естественных единицах
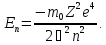
В общем случае решение радиального уравнения Шредингера для атомов выполняется численно, что связано с необходимостью учета внутриатомных эффектов взаимодействия между электронами.
