Кривые второго порядка

Окружность – геометрическое место точек, расстояния от которых до одной фиксированной (центра) равны.

Применим метод координат для того, чтобы вывести алгебраическое уравнение окружности.

Пусть - центр окружности. Возьмём такое, что точка M принадлежит нашей окружности. Тогда или .

Эллипс – геометрическое место точек, сумма расстояний от которых до двух фиксированных (полюсов) равны.

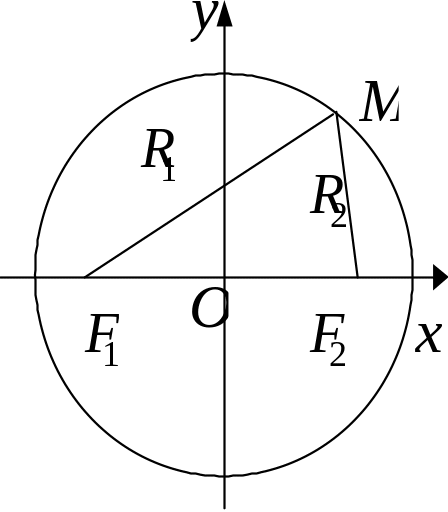. Введём систему координат так, как показано на рисунке. Здесь , , ­ . Такую систему координат называют канонической. Тогда , . Возьмём любую точку , принадлежащую нашему эллипсу. Тогда Преобразуем это выражение: , , . Сложим теперь его с исходным: , , , , . Обозначив , получим каноническое уравнение эллипса: . Здесь a и b равны соответственно горизонтальной и вертикальной полуосям эллипса. Отсюда уравнение эллипса в явном виде: .

1. Если , то уравнение эллипса представляет собой окружность.

2. Эллипс имеет две оси симметрии (Ox и Oy) и центр симметрии ( ).

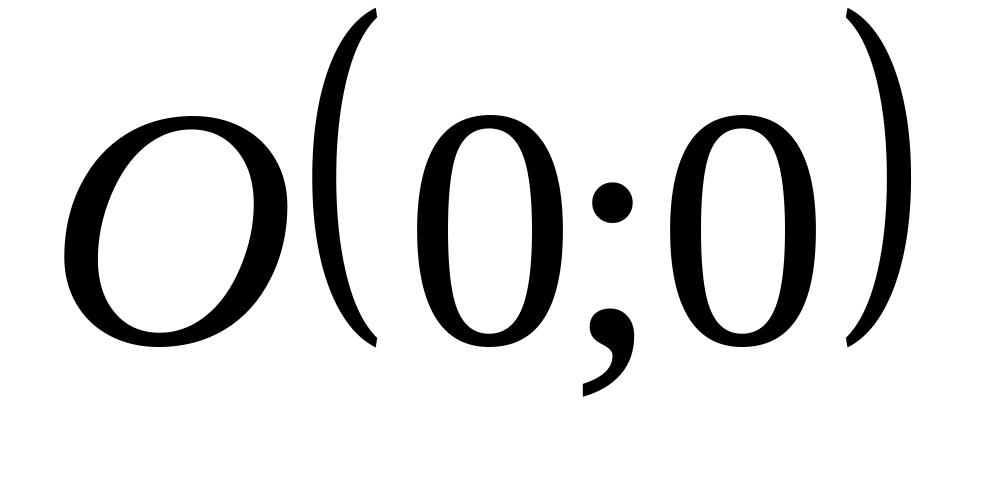3. Эллипс – непрерывная кривая.

4. Ограниченная кривая, , .

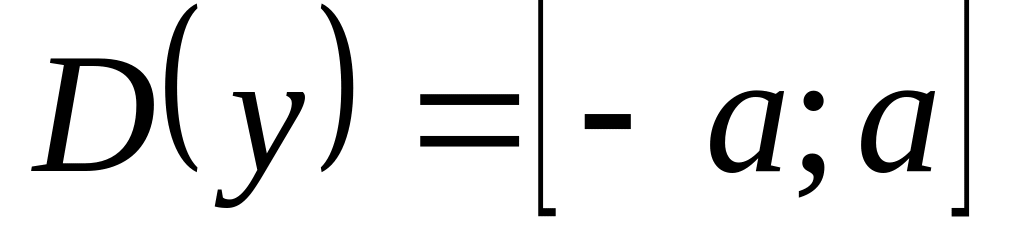5. Гладкая кривая (во всех точках имеет касательную).

6. Уравнение касательной для эллипса: .

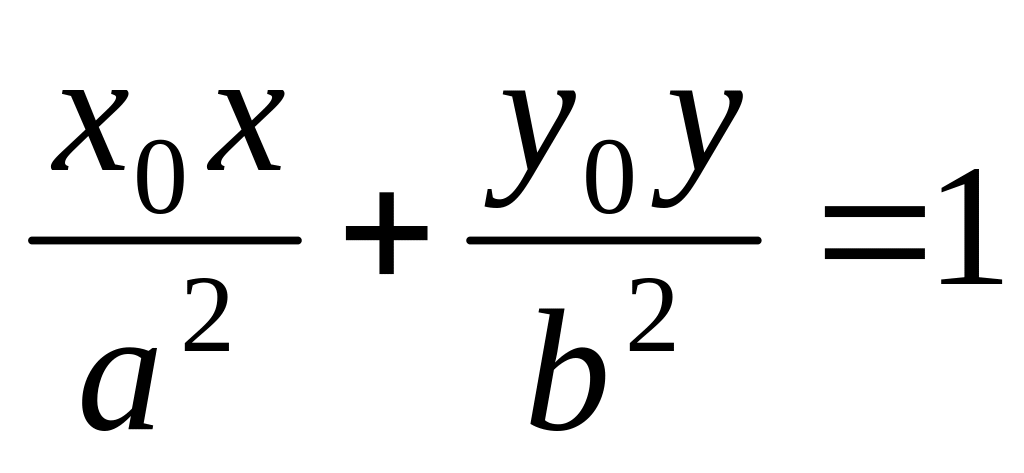7. Верхняя половина эллипса выпукла вверх, нижняя – вниз.

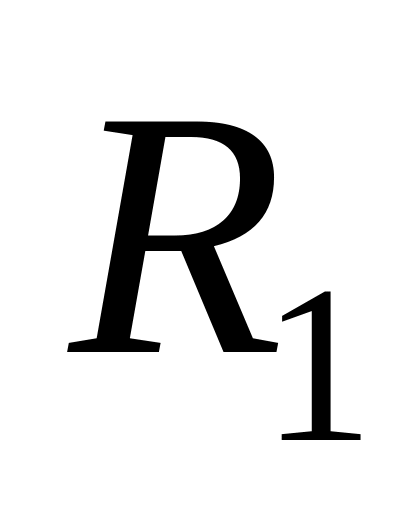8. и 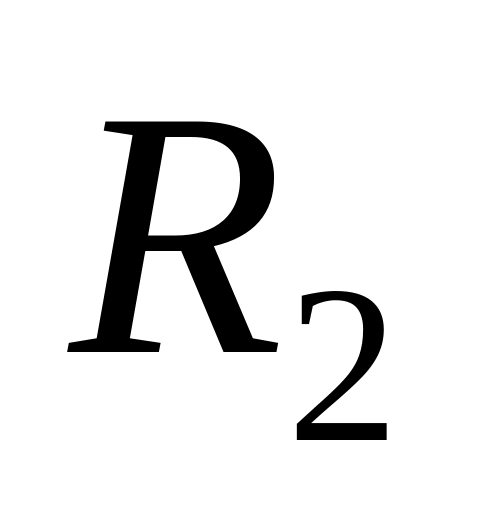называются фокальными радиусами.

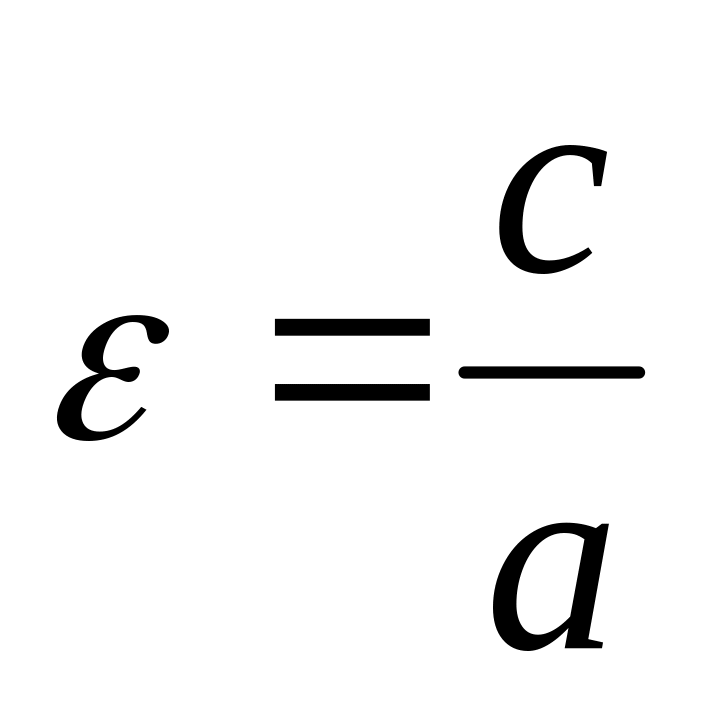9. - эксцентриситет эллипса, .

10. , .

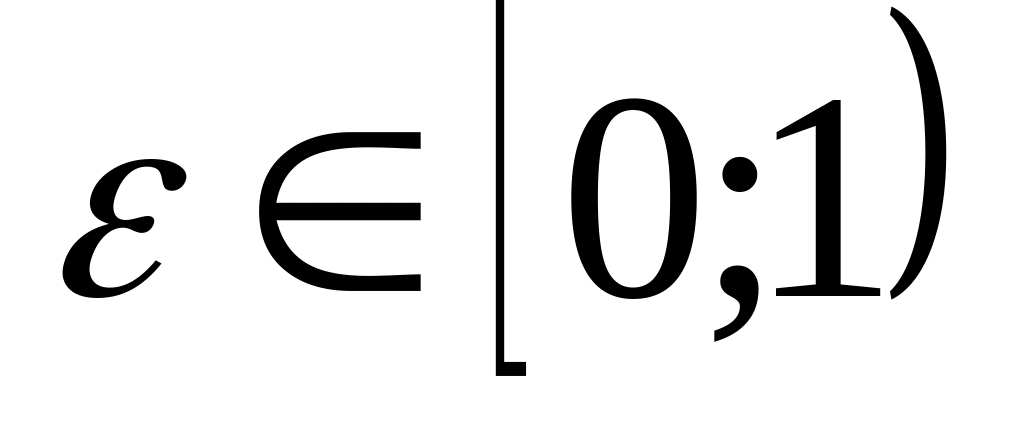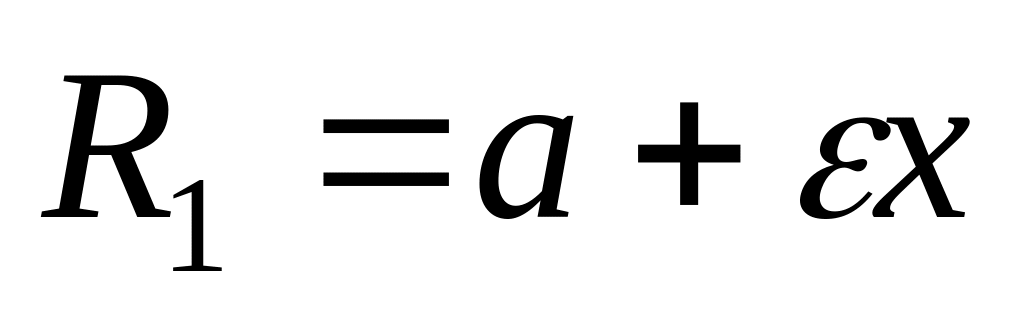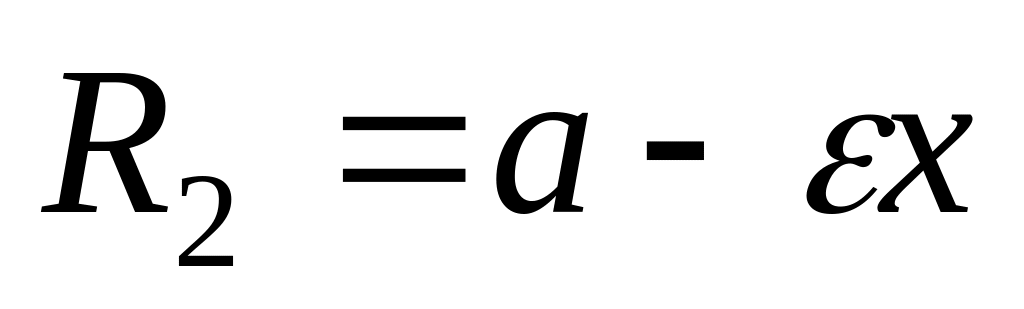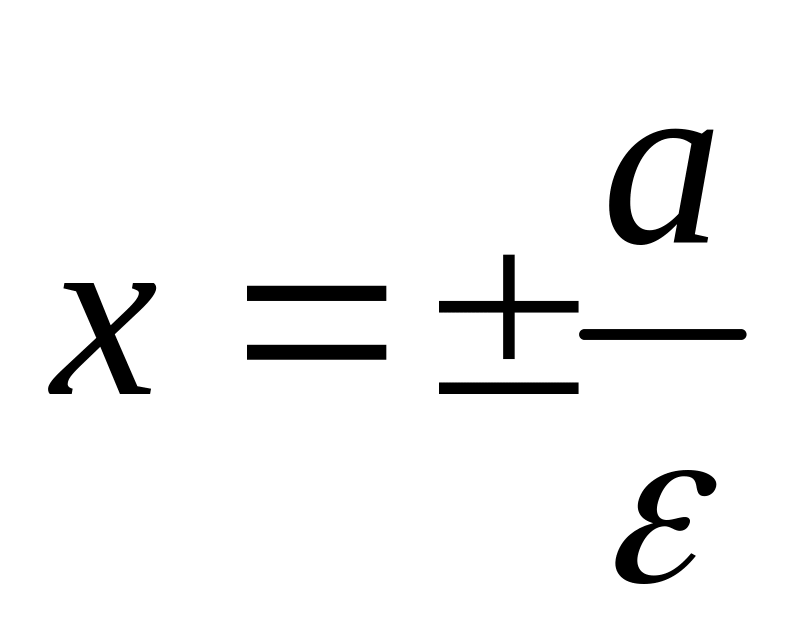11. - директрисы эллипса.

12. Оптическое свойство эллипса: если поместить источник света в один из фокусов, то после отражения от эллипса как от зеркала все лучи пройдут через другой фокус.

Гипербола – геометрическое место точек, абсолютные величины разности расстояний от которых до двух фиксированных (фокусов) равны.

В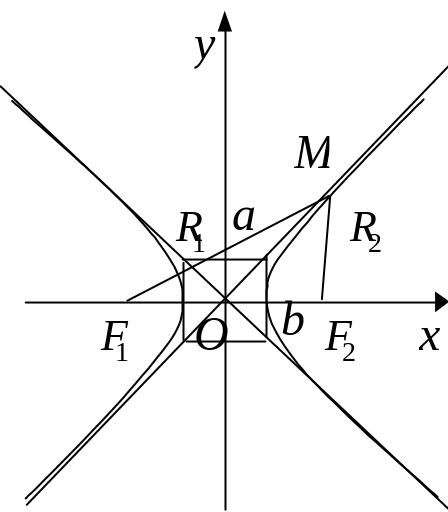 ведём систему координат так, как показано на рисунке. Здесь, так же, как и у эллипса, , т.е. , . Такая система координат называется канонической. Условие гиперболы записывается так: или . Избавившись от иррациональности (см. вывод уравнение эллипса выше), получим: , где . Уравнение гиперболы в явном виде: .

1. Гипербола имеет две оси симметрии (Ox и Oy) и центр симметрии ( ).

2. Гипербола – гладкая кривая.

3. Уравнение касательной для гиперболы: .

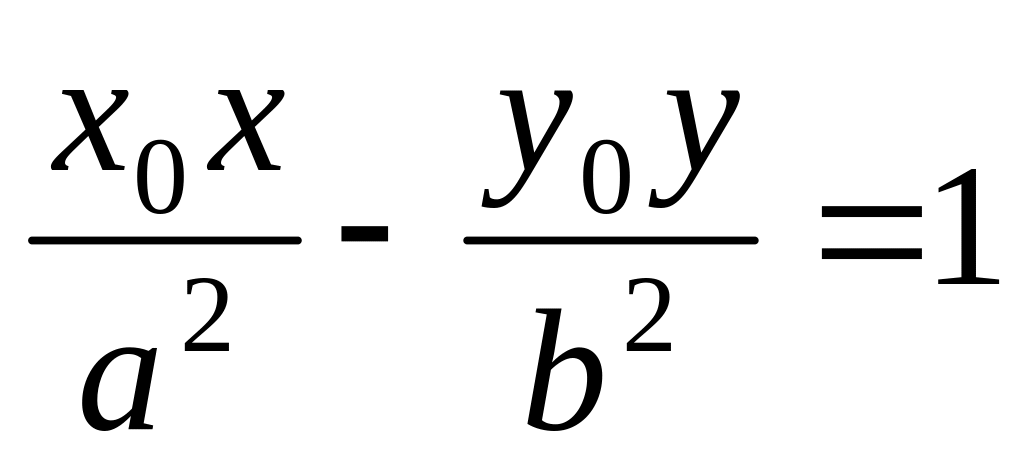4. Гипербола, задающаяся уравнением 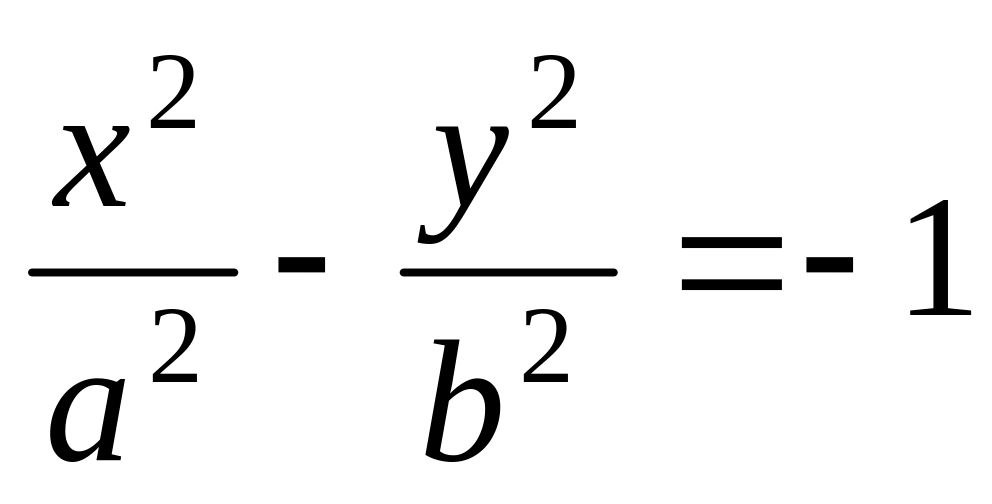, называется сопряжённой для исследуемой гиперболы.

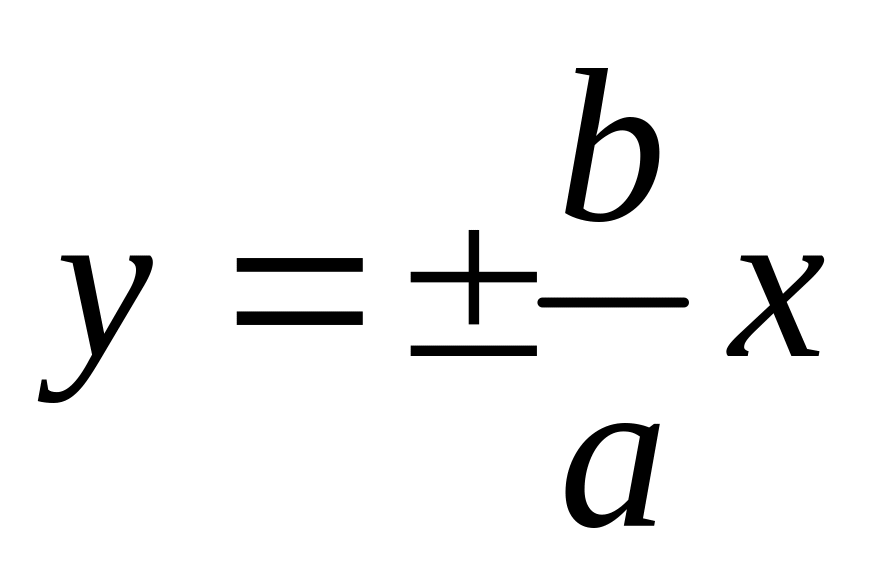5. - асимптоты гиперболы.

6. и - фокальные радиусы.

7. Эксцентриситет гиперболы , .

8. , .

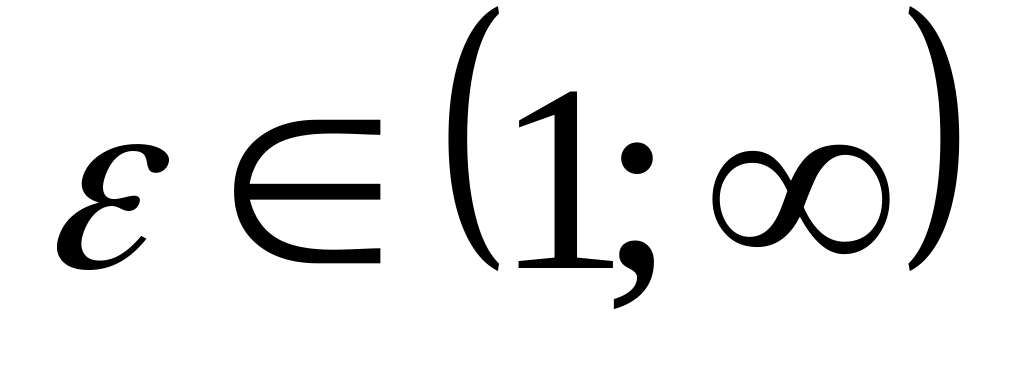9. - директрисы гиперболы.

10. Оптические свойства гиперболы: если поместить в один из фокусов гиперболы источник света, то все лучи, им испущенные, после отражения от гиперболы пойдут по прямой проходящей через другой фокус.

Парабола – геометрическое место точек, расстояния от которых до одной фиксированной и до фиксированной прямой, называемой директрисой, равны.

В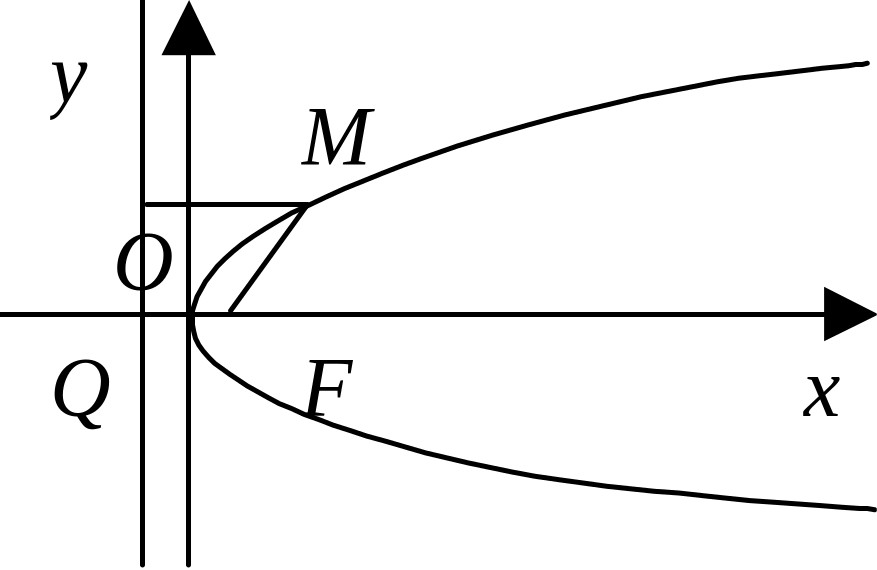 ведём систему координат так, как показано на рисунке. Здесь . Такая система координат называется канонической. Тогда условие параболы запишется так: . Избавившись от иррациональности, получим: - каноническое уравнение параболы. Уравнение параболы в явном виде: .

1. Парабола имеет ось симметрии (Ox).

2. , .

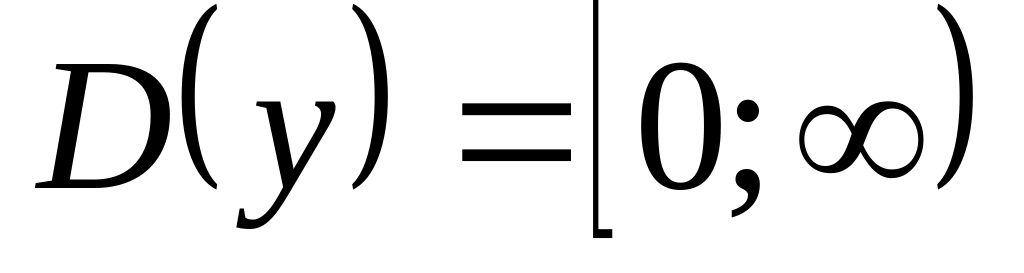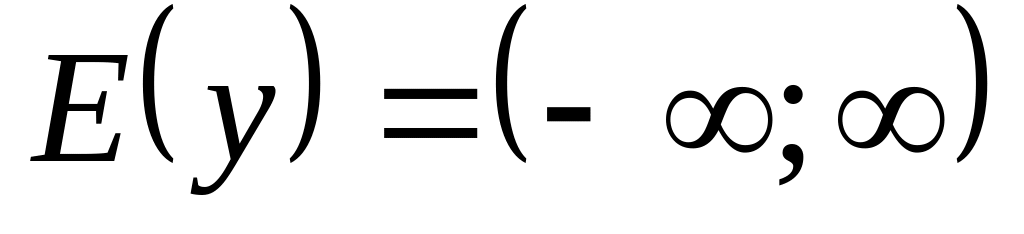3. Эксцентриситет параболы .

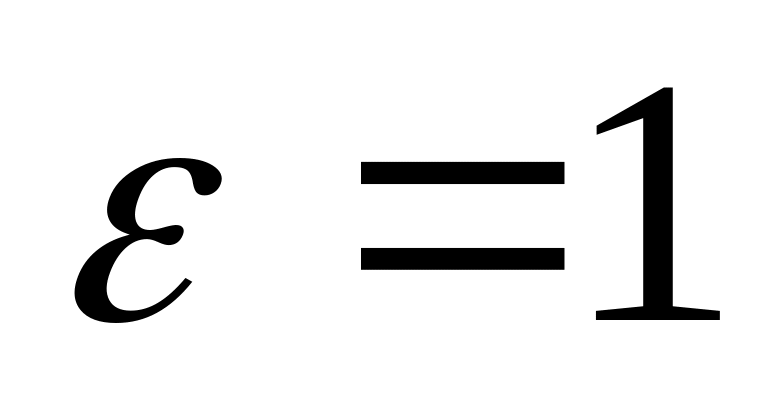Общее уравнение кривой второго порядка: . Любая кривая второго порядка описывается таким уравнением и наоборот. Все кривые второго порядка могут быть разделены на две группы: невырожденные (эллипс, гипербола, параболы) и вырожденные. Пример вырожденной кривой: .

Поверхности второго порядка

Цилиндрические

Цилиндрические поверхности – поверхности, образованные прямыми, параллельными некоторой фиксированной прямой. Эта прямая называется осью. Прямые, с помощью которых образована цилиндрическая поверхность – образующими. Кривая, лежащая на цилиндрической поверхности и проходящая через все образующие называется направляющей.

Если ось цилиндрической поверхности параллельна, к примеру, Ox, то уравнение этой поверхности не будет содержать переменной x.

- уравнение кругового цилиндра, - уравнение эллиптического цилиндра, - уравнение гиперболического цилиндра, - уравнение параболического цилиндра.