
Прямая на плоскости
Составим уравнение прямой, проходящей
через данную точку
![]() и перпендикулярно данному вектору
и перпендикулярно данному вектору
![]() .
.
З апишем
условие принадлежности точки
апишем
условие принадлежности точки
![]() прямой l:
прямой l:
![]() .
Это значит, что
.
Это значит, что
![]() - векторное уравнение прямой, проходящей
через точку
- векторное уравнение прямой, проходящей
через точку
![]() .
.
![]() .
Обозначив
.
Обозначив
![]() ,
получим:
,
получим:
![]() - общее уравнение прямой, если
- общее уравнение прямой, если
![]() или
или
![]() .
.
Ненулевой вектор, перпендикулярной данной прямой называют нормальным вектором прямой.
Приняв
![]() и
и
![]() ,
можно получить уравнение
,
можно получить уравнение
![]() .
При этом
.
При этом
![]() ,
где - угол
наклона прямой к положительному
направлению оси Ox, а
b = величина отрезка,
отсекаемого прямой на оси Oy.
,
где - угол
наклона прямой к положительному
направлению оси Ox, а
b = величина отрезка,
отсекаемого прямой на оси Oy.
Составим теперь уравнение прямой,
проходящей через данную точку
параллельно
![]() .
.
З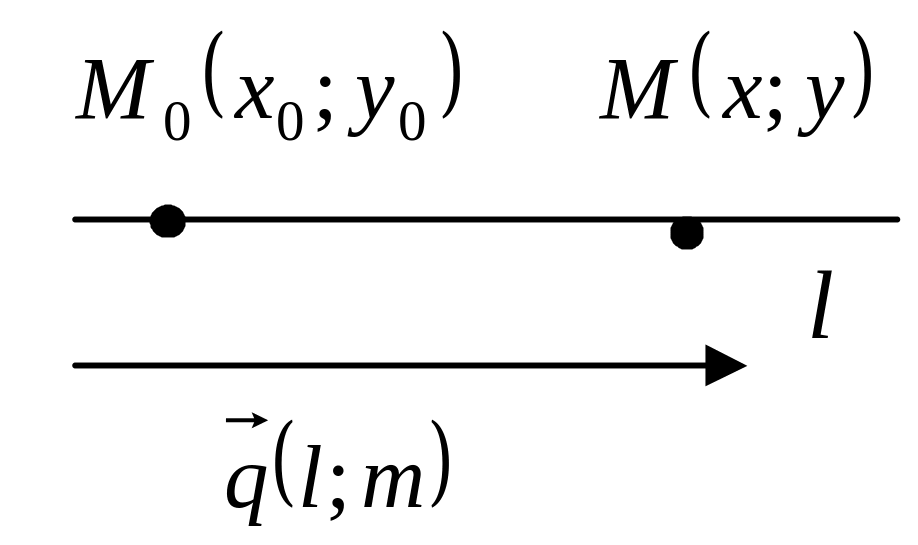 апишем
условие принадлежности точки
прямой l:
апишем
условие принадлежности точки
прямой l:
![]() .
Это значит, что
.
Это значит, что
![]() - векторное уравнение прямой. Раз
,
то
- векторное уравнение прямой. Раз
,
то
![]() - каноническое уравнение прямой.
- каноническое уравнение прямой.
Ненулевой вектор, параллельный данной прямой, называют направляющим вектором этой прямой.
Уравнение прямой, проходящей через две
данные точки
![]() и
и
![]() .
В качестве точки
.
В качестве точки
![]() возьмём одну из них, а в качестве
возьмём одну из них, а в качестве
![]() возьмём
.
Тогда
возьмём
.
Тогда
![]() - уравнение прямой, проходящей через
две данные точки.
- уравнение прямой, проходящей через
две данные точки.
Если мы преобразуем канонические
уравнения прямой следующим образом:
![]()
![]() ,
то получим
,
то получим
![]() - параметрические уравнения прямой.
- параметрические уравнения прямой.
Угол между прямыми
Это угол, на который нужно повернуть одну прямую до совмещения её с другой прямой.
Пусть
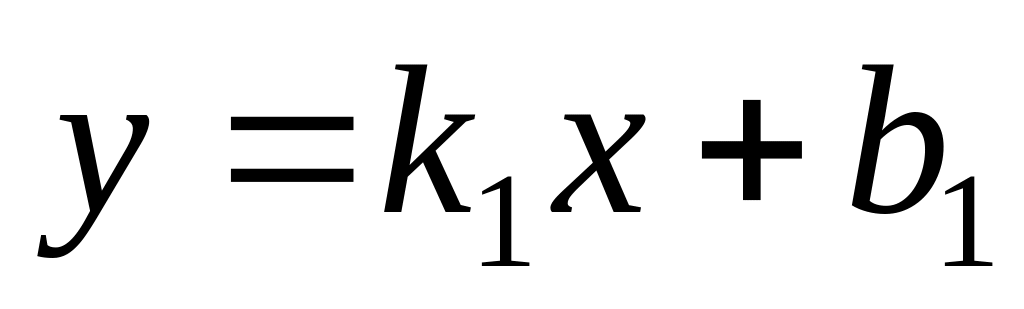 ,
,
 .
Тогда
.
Тогда
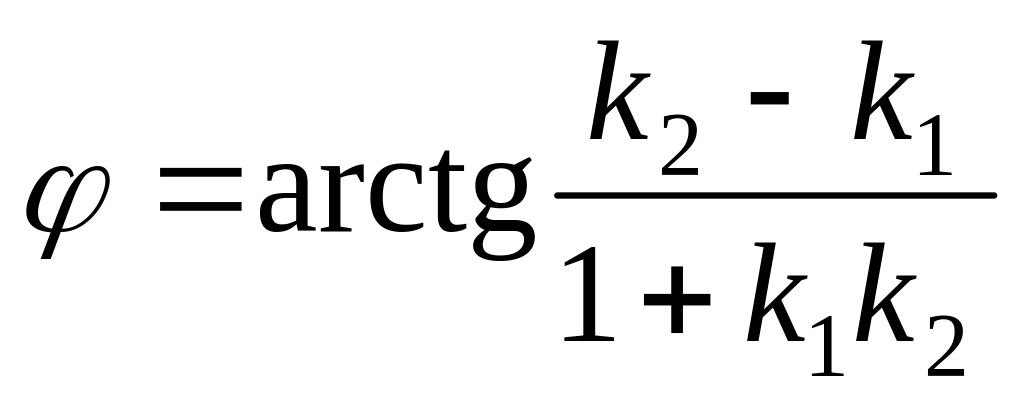 .
.Пусть
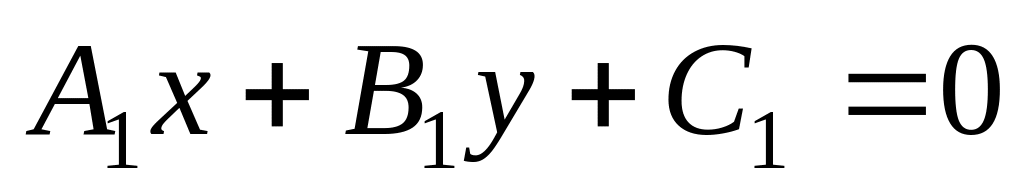 ,
,
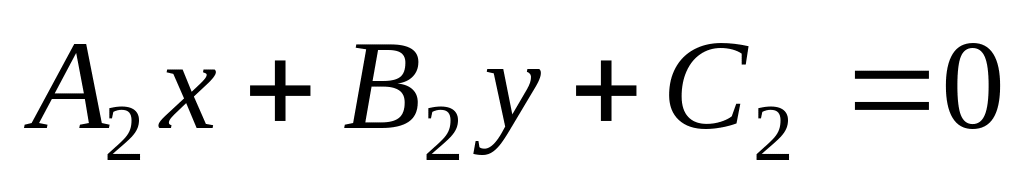 .
Тогда
.
Тогда
 .
.Пусть
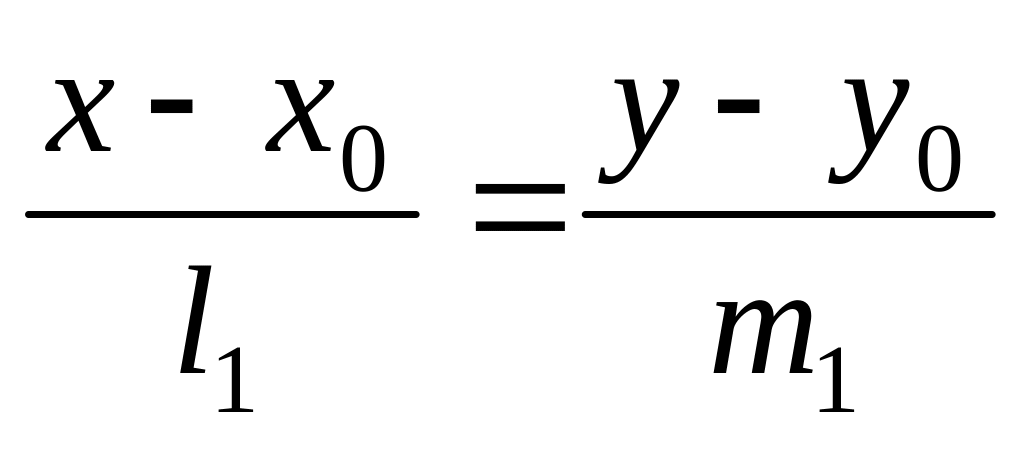 ,
,
 .
Тогда
.
Тогда
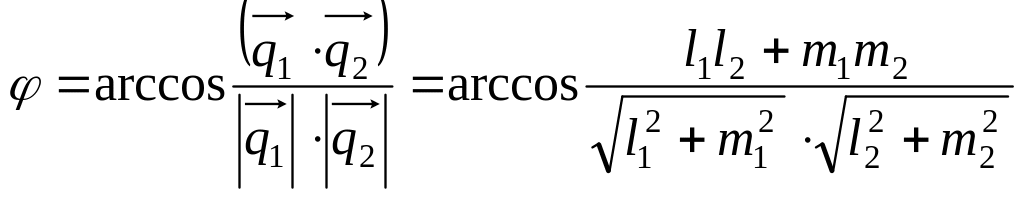 .
.
Полные и неполные уравнения прямой
Общее уравнение прямой
![]() называют полным, если
,
и
называют полным, если
,
и
![]() .
.
Полное уравнение прямой можно привести
к уравнению прямой в отрезках: обозначим
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Здесь a и b
– величины отрезков, отсекаемых прямой
на осях Ox и Oy
соответственно.
.
Здесь a и b
– величины отрезков, отсекаемых прямой
на осях Ox и Oy
соответственно.
Неполные уравнения прямой:
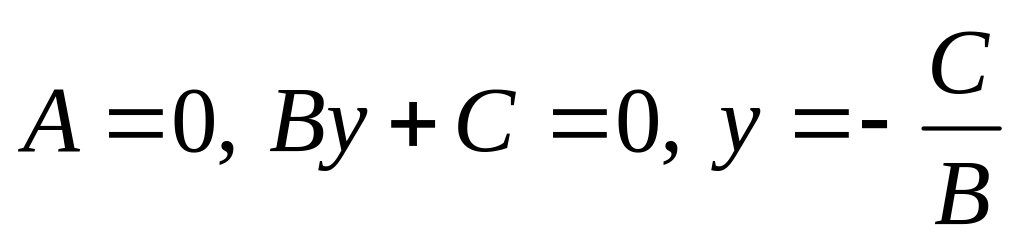 – параллельна оси x.
– параллельна оси x. – параллельна оси y.
– параллельна оси y.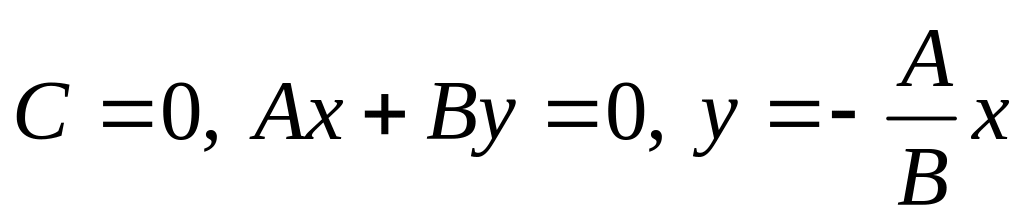 – проходит через начало координат.
– проходит через начало координат.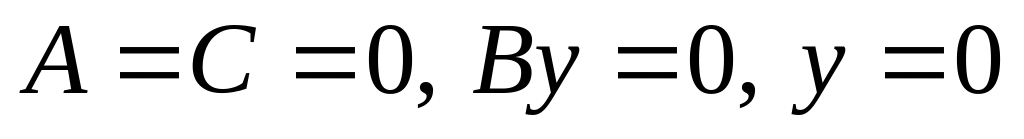 – ось x.
– ось x.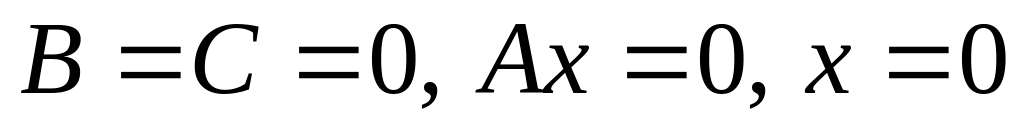 – ось y.
– ось y.
Нормальное уравнения прямой
это уравнение прямой
![]() ,
,
![]() ,
где
- угол между нормалью к прямой и осью
Ox,
причём нормаль направлена из начала
координат в сторону прямой и p
– расстояние от начала координат до
прямой.
,
где
- угол между нормалью к прямой и осью
Ox,
причём нормаль направлена из начала
координат в сторону прямой и p
– расстояние от начала координат до
прямой.
Нормальное уравнение прямой получается из полного следующим образом:
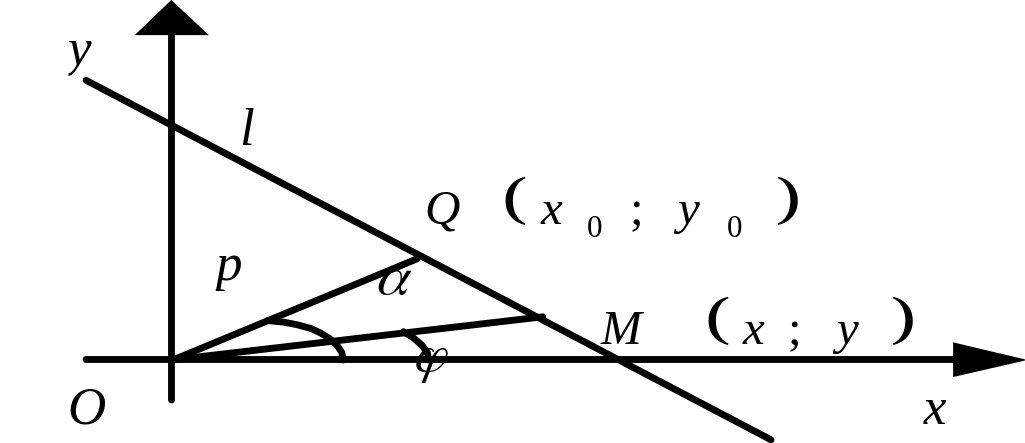
Вывод нормального уравнения прямой:
Введём сразу две системы координат –
полярную и цилиндрическую так, чтобы
их начала совпадали, и ось полярной
системы совпадала с осью Ox
цилиндрической. Тогда выражение
![]() справедливо для
справедливо для
![]() .
Преобразуем это выражение:
.
Преобразуем это выражение:
![]() (Т.к.
(Т.к.![]() и
и
![]() ),
или
.
),
или
.
Нормальное уравнение прямой применяется
для вычисления расстояния от данной
точки плоскости до прямой. 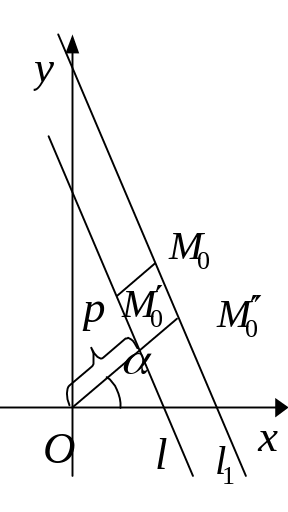 Рассмотрим
случай, когда точка
и точка O лежат по одну
сторону от прямой. Расстояние от
Рассмотрим
случай, когда точка
и точка O лежат по одну
сторону от прямой. Расстояние от
![]() то l равно
то l равно
![]() .
Рассмотрим нормальное уравнение прямой,
параллельной l (
.
Рассмотрим нормальное уравнение прямой,
параллельной l (![]() ):
):
![]() ,
где
,
где
![]() .
Т.к. точка
.
Т.к. точка
![]() ,
то
,
то
![]() – верное равенство, значит,
– верное равенство, значит,
![]() .
.
![]() .
Если точка
и точка O лежат по одну
сторону от прямой l,
то расстояние от
до l равно
.
Если точка
и точка O лежат по одну
сторону от прямой l,
то расстояние от
до l равно
![]() .
Следовательно, расстояние от
до l равно
.
Следовательно, расстояние от
до l равно
![]() .
.
Приведём общее уравнение прямой к
нормальному виду (
к
![]() ).
Очевидно, что коэффициенты пропорциональны,
т.е.
).
Очевидно, что коэффициенты пропорциональны,
т.е.
![]() .
Тогда
.
Тогда
![]()
![]() и знак
противоположен знаку C.
и знак
противоположен знаку C.
Отклонением точки от прямой
называется расстояние от этой точки до
прямой, взятое со знаком «+», если эта
точка и начало координат располагаются
по одну сторону от прямой и «–» - если
по разные стороны, т.е. отклонение равно
![]() .
.
С помощью нормальных уравнений прямой можно составлять уравнения биссектрис, образованных двумя прямыми:
Пусть
- первая прямая,
![]() - вторая прямая. Для того чтобы получить
одну из биссектрис, необходимо приравнять
левые части уравнений:
- вторая прямая. Для того чтобы получить
одну из биссектрис, необходимо приравнять
левые части уравнений:
![]()
![]() .
Для второй:
.
Для второй:
![]() .
.
