§ 14. Односторонние пределы

Определение 1 (Гейне). ЧислоА называетсяправым пределом функциив точке(или пределом функциив точкесправа), если для любой последовательности значений аргумента, сходящейся ки такой, что, соответствующая последовательность значений функциисходится к числуА.

Определение 2 (Коши). ЧислоА называетсяправым пределом функциив точке(или пределом функциив точкесправа), если для любогонайдется, такое, что для всех значений аргументах, удовлетворяющих неравенству

,

выполняется неравенство

.

Пишут: , а если, то, или, короче,и.

Совершенно аналогично даются определения односторонних пределов слева. Пишут: или.

Пример 1. Пусть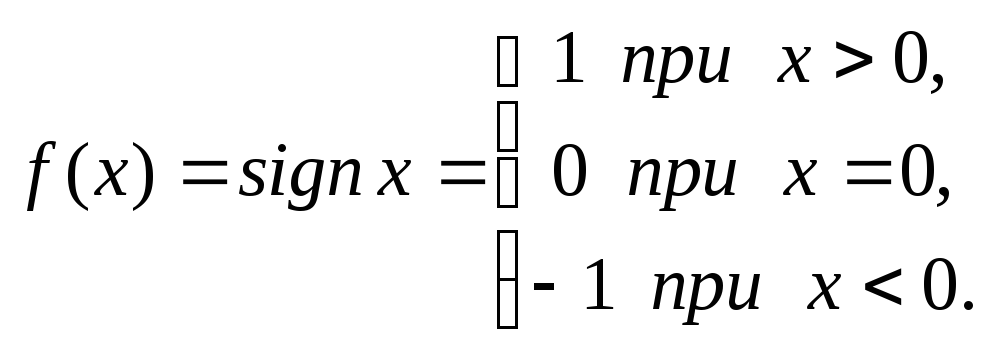Тогда,, поэтомуне существует.

Имеет место

Теорема 1. Для того чтобы функцияимела предел в точке, необходимо и достаточно, чтобы она имела в этой точке равные односторонние пределы. При этом

.

Это достаточно очевидно.

Введем теперь понятие предела функции на бесконечности.

Определение 3 (Гейне). ЧислоА называется пределом функциипри, если для любой бесконечно большой последовательностипоследовательность значенийсходится к числуА.

Определение 4 (Коши). ЧислоА называется пределом функциипри, если для любогонайдется, такое, что для всех значений аргументах, удовлетворяющих неравенству, выполняется неравенство.

Пишут: .

Докажем, например, что . Пусть– произвольная бесконечно большая последовательность. Тогда, как известно,– бесконечно малая последовательность, поэтомупо определению 3.

Аналогично теореме 1 § 13 можно доказать эквивалентность определений 3 и 4. Справедлив также критерий Коши существования предела функции, когда .

Подобным же образом определяются пределы функции при ипо Коши и по Гейне.

§ 15. Арифметические операции над функциями, имеющими предел

Теорема 1. Пусть функцииизаданы на одном и том же множествеХ и имеют в точкепределы, равные соответственноа иb. Тогда

.

Доказательство. Пусть– произвольная сходящаяся кпоследовательность,. Тогда, в силу определения предела функции в точкепо Гейне,и по свойствам сходящихся последовательностей,

. Так как последовательностьвыбиралась

произвольно, то, в силу определения предела по Гейне, теорема доказана.

Аналогичные теоремы имеют место в случае, когда ,,и для односторонних пределов.

Пример 1. С помощью теоремы 1 вычисляются следующие пределы:

– доказывается методом математической индукции,,при условии, что,.

Заметим, что для действительных функций имеют место теорема о промежуточной переменной и переход к пределу в неравенствах. Доказываются они с помощью соответствующих утверждений для последовательностей и определений предела по Гейне.

§ 16. Бесконечно малые и бесконечно большие функции. Первый замечательный предел

Определение 1. Функцияназываетсябесконечно малой в окрестности точки , если.

Например, – бесконечно малая функция в окрестности точки, так как.

Теорема 1. Для того чтобы, необходимо и достаточно, чтобы имело место представление, где– бесконечно малая в окрестности точкифункция.

Доказательство. Необходимость. Пусть. Положим.

Тогда – бесконечно малая в окрестности точкифункция и.

Достаточность. Пусть, где– бесконечно малая в окрестности точкифункция. Тогда. Теорема доказана.

Остановимся на сравнении бесконечно малых функций.

Определение 2. Говорят, что функциииявляютсяэквивалентными бесконечно малыми в окрестности точкифункциями, если.

Пишут: ~при.

Определение 3. Говорят, что функциииявляются в окрестности точкибесконечно малыми функциямиодного порядка, если. Если же, то говорят, чтоявляется в окрестности точкибесконечно малойболее высокого порядка, чем.

Покажем, что при.

Теорема 2 (первый замечательный предел). Справедливо равенство.

Д

С

В

D A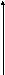

оказательство. Построим единичный круг и центральный угол.

Видим, что

. (16.1)

Имеем

,(16.2)

, (16.3)

О

x

. (16.4)

Из (16.1)–(16.4) получаем

.

Разделив последнее неравенство на , получим

. (16.5)

Разделив на каждую из частей этого неравенства, имеем

. (16.6)

Поскольку 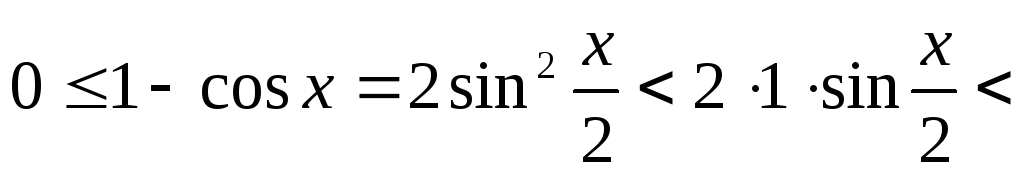(см. (16.5))и, по

Теореме о промежуточной переменной , то есть. А так как

– функция четная, то. Поэтому

. (16.7)

Учитывая, что неравенство (16.6) сохраняется и для в силу четности всех входящих в него функций, из (16.7) и теоремы о промежуточной переменной получаем. Теорема доказана.

Установим теперь следствия первого замечательного предела. Покажем, что при . Имеем

при;

при;

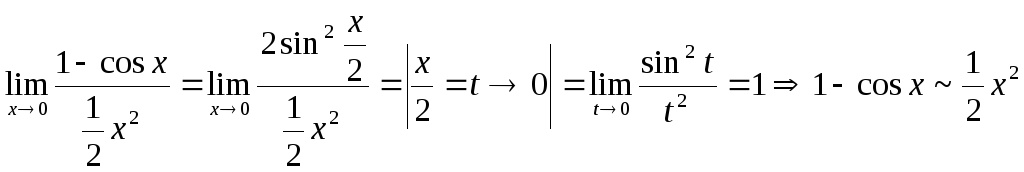при;

при.

При раскрытии неопределенностей типа полезна

Теорема 3. Если– бесконечно малые функции в окрестности точкии, то

.

Доказательство. Имеем

. Теорема доказана.

Например, .

Замечание. В тех случаях, когда в числителе или знаменателе записана сумма, при раскрытии неопределенностей нельзя заменять отдельные слагаемые эквивалентными функциями, так как такая замена может привести к неверному результату. Например, в пределенельзя заменитьнаинах, так как получается выражение, не имеющее смысла. Правильно вычислять предел так:

.

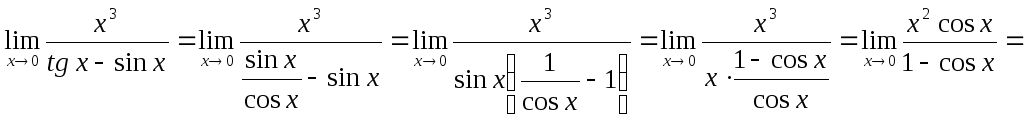
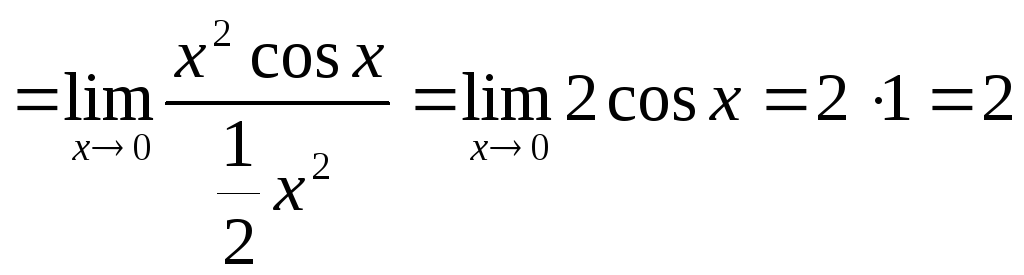Рассмотрим теперь бесконечно большие функции.

Определение 4. Если для любой последовательности значений аргумента, сходящейся к, то говорят, что функцияимеет в точкебесконечный предел, а функциюназываютбесконечно большой при . Пишут:.

Можно дать равносильное

Определение . Говорят, что функцияимеет в точкебесконечный предел, если для любого числанайдется такое число, что для всех значений, удовлетворяющих неравенству, выполняется неравенство. В этом случаеназывается бесконечно большой функцией в точке.

Аналогично определяются соотношения ,.

Сравнивают бесконечно большие функции так же, как и бесконечно малые функции.

Определение 5. Еслии– бесконечно большие функции при и, то говорят, что– бесконечно большаяболее высокого порядка, чем. Говорят, что функциииимеют одинаковый порядок роста, если.

Например, для функций и, бесконечно больших при, имеем, поэтому функциииимеют одинаковый порядок роста.