Міністерство освіти і науки, молоді та спорту України

Українська академія друкарства

Кафедра математики і фізики

Теорія випадкових процесів індивідуальні домашні завдання для студентів інженерних спеціальностей

Львів, ­2012

Пирч Н. М. Теорія випадкових процесів: індивідуальні домашні завдання для студ. інженерних / Н. М. Пирч. ─ Львів : Українська академія друкарства, 2012. ─ 23 с.

Затверджено кафедрою математики і фізики Української академії друкарства (протокол № 1 від 14 червня 2012 року).

Автор:

Пирч Н. М., канд. фіз.-мат. наук, доцент

Автор висловлює щиру подяку Петрові Степановичу Сеньо за допомогу та цінні поради, висловлені при написанні даної роботи

Відповідальний за випуск:

Кульчицький А. Д., канд. фіз-мат. наук, доцент

Верстання:

Шевчук Г. Я.

Завдання № 1

Для випадкового процесу знайти

1. одновимірну функцію розподілу ;

2. одновимірну щільність розподілу ;

3. математичне сподівання ;

4. дисперсію ;

5. середнє квадратичне відхилення ;

6. флуктуаційну складову ;

7. кореляційну функцію ;

8. нормовану кореляційну функцію ;

9. записати випадковий процес ;

10. записати випадковий процес .

1. , де − випадкова величина, що має нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням

2. , де − випадкова величина, що має показниковий розподіл з параметром

3. , де − випадкова величина, рівномірно розподілена на відрізку [1,3]

4. , де − випадкова величина, що має функцію розподілу

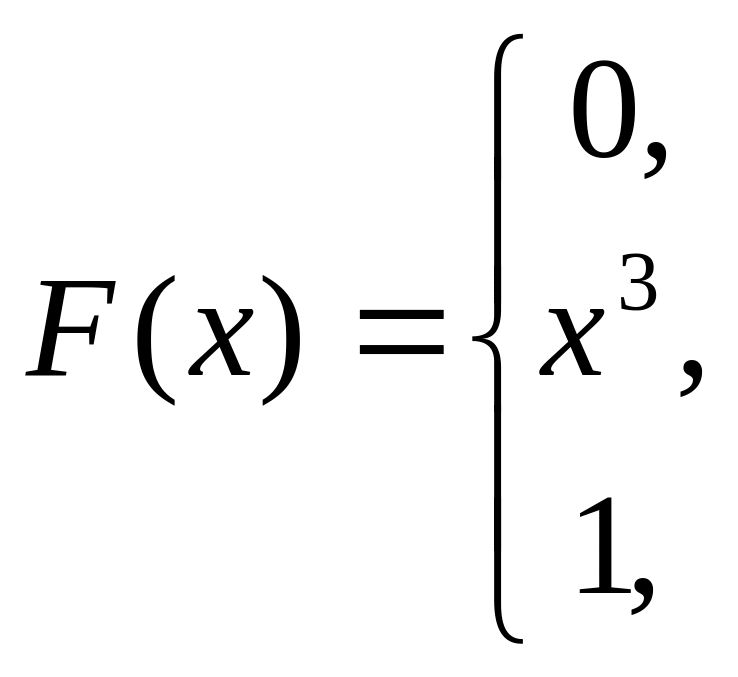
5. , де − випадкова величина, що має функцію розподілу

6. , де − випадкова величина, що має функцію розподілу

7. , де − випадкова величина, що має функцію розподілу

8. , де − випадкова величина, що має функцію розподілу

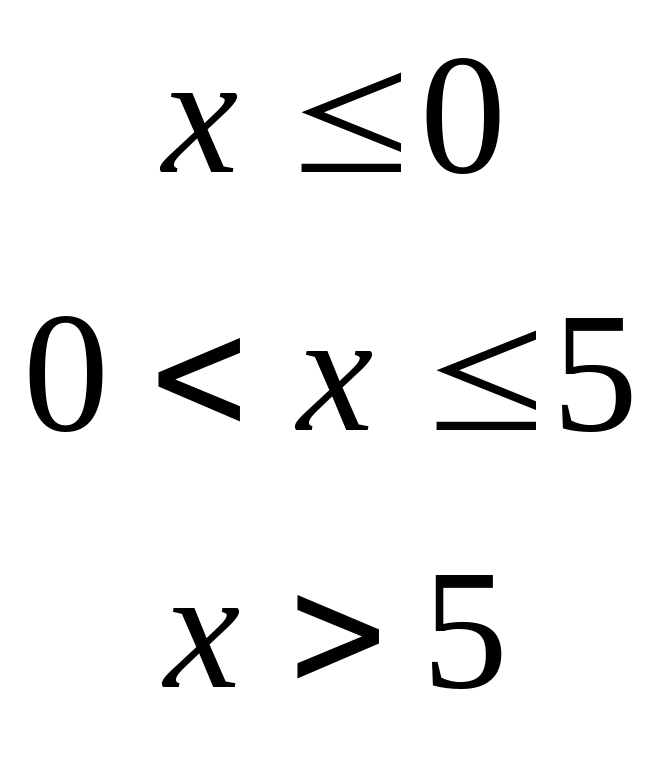
9. , де − випадкова величина, що має функцію розподілу

10. , де − випадкова величина, що має функцію розподілу

11. , де − випадкова величина, що має функцію розподілу

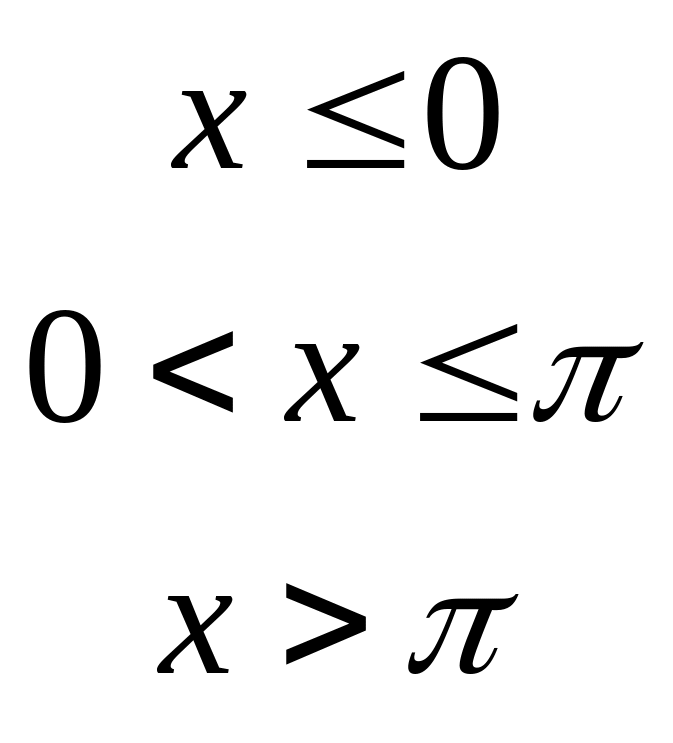
12. , − випадкова величина, що має функцію розподілу

13. , де − випадкова величина, що має нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням

14. , де − випадкова величина, що має показниковий розподіл з параметром

15. , де − випадкова величина, рівномірно розподілена на відрізку [-1,2]

16. , де − випадкова величина, що має функцію розподілу

17. , де − випадкова величина, що має функцію розподілу

18. , де − випадкова величина, що має функцію розподілу

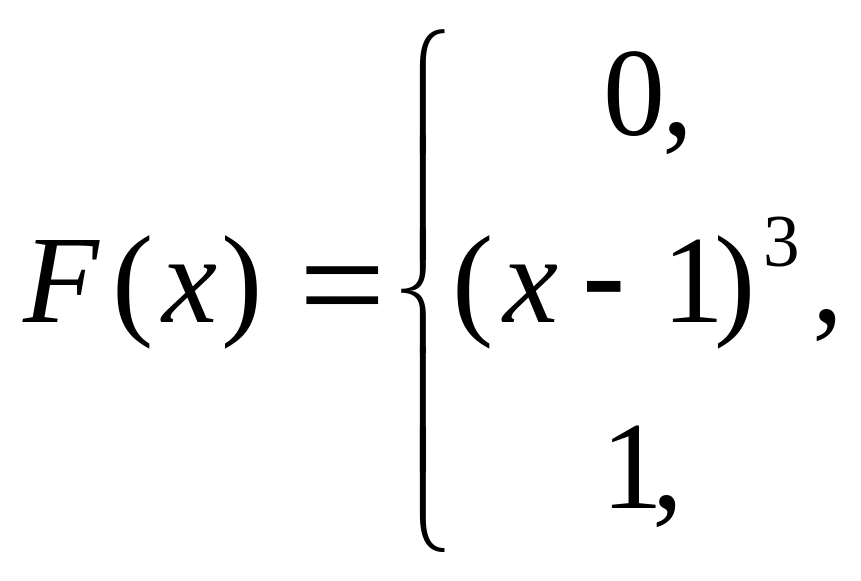
19. , де − випадкова величина, що має функцію розподілу

20. , де − випадкова величина, що має функцію розподілу

21. , де − випадкова величина, що має функцію розподілу

22. , де − випадкова величина, що має функцію розподілу

23. , де − випадкова величина, що має функцію розподілу

24. , де − випадкова величина, що має функцію розподілу

25. , де − випадкова величина, що має функцію розподілу

26. , де − випадкова величина, що має функцію розподілу

27. , де − випадкова величина, що має функцію розподілу

28. , де − випадкова величина, що має нормальний розподіл з математичним сподіванням і середнім квадратичним відхиленням

29. , де − випадкова величина, що має показниковий розподіл з параметром

30. , де − випадкова величина, рівномірно розподілена на відрізку [0,5].

Завдання № 2

Задано однорідний ланцюг Маркова з матрицею однокрокових ймовірностей переходу та початковим розподілом ймовірностей .

1. Знайти розподіл ймовірностей .

2. Зобразити ймовірнісний граф даного ланцюга Маркова.

3. Знайти граничний розподіл ймовірностей.

4. Знайти ймовірність того, що в момент часу перебуватиме у стані , якщо відомо, що в момент часу система перебуває у стані .

5. Знайти ймовірність того, що від моменту часу до моменту часу система не змінить свого стану.

6*. Нехай − ймовірність того, що в момент часу система знаходиться у стані , − ймовірність того, що в момент часу система знаходиться у стані , − ймовірність того, що в момент часу система знаходиться у стані ,. Для послідовностей , та скласти систему рекурентних співвідношень та знайти її розв’язок.

1.

2.

3.

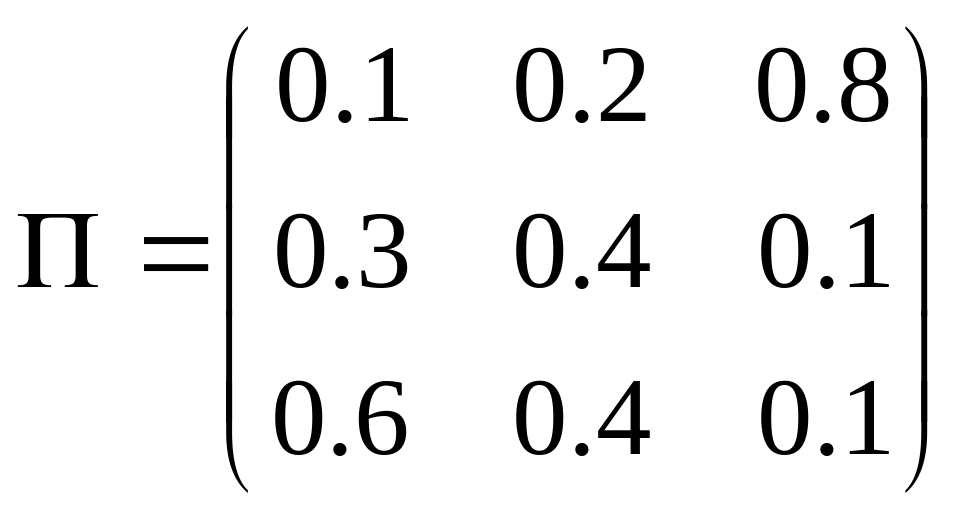
4.

5.

6.

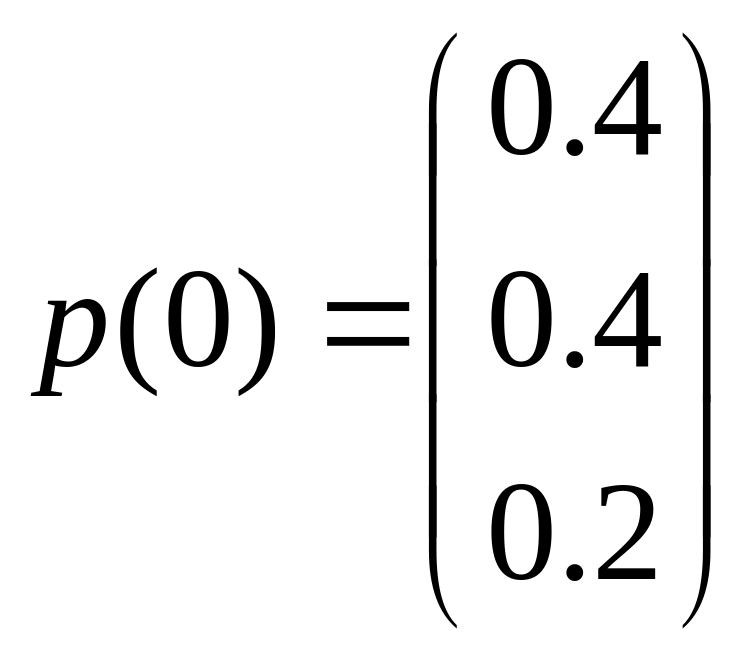
7.

8.

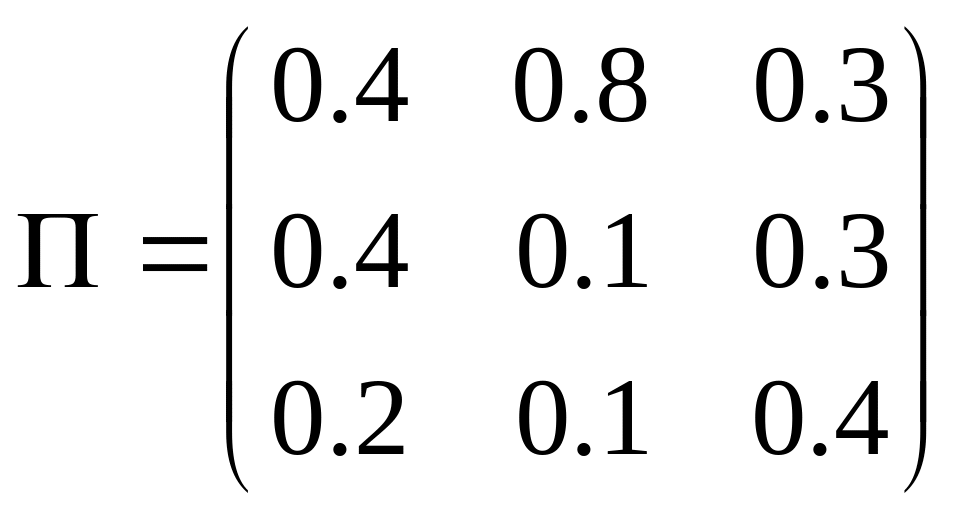
9.

10.

11.

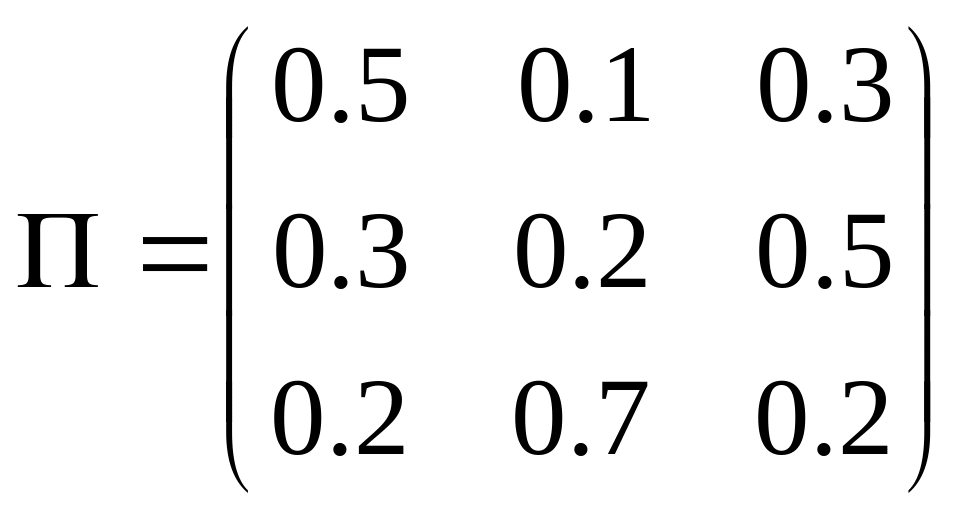
12.

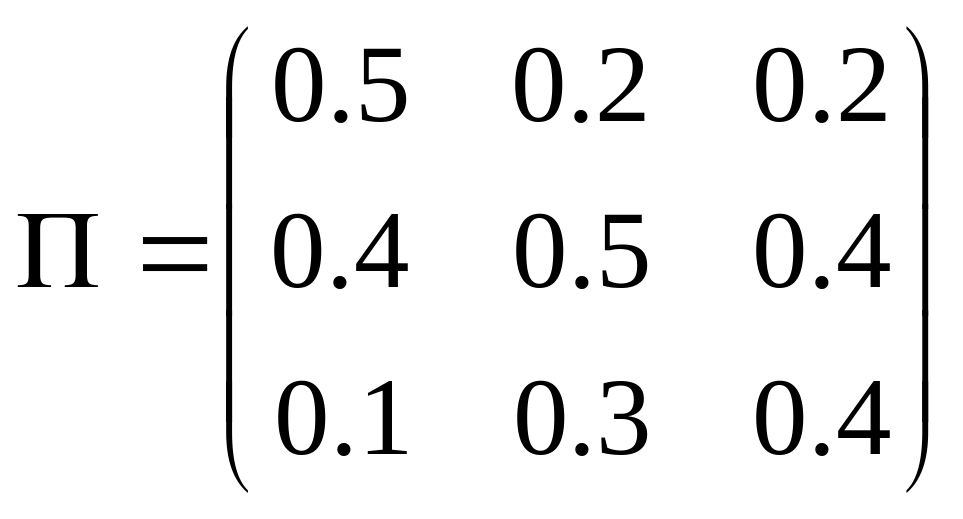
13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

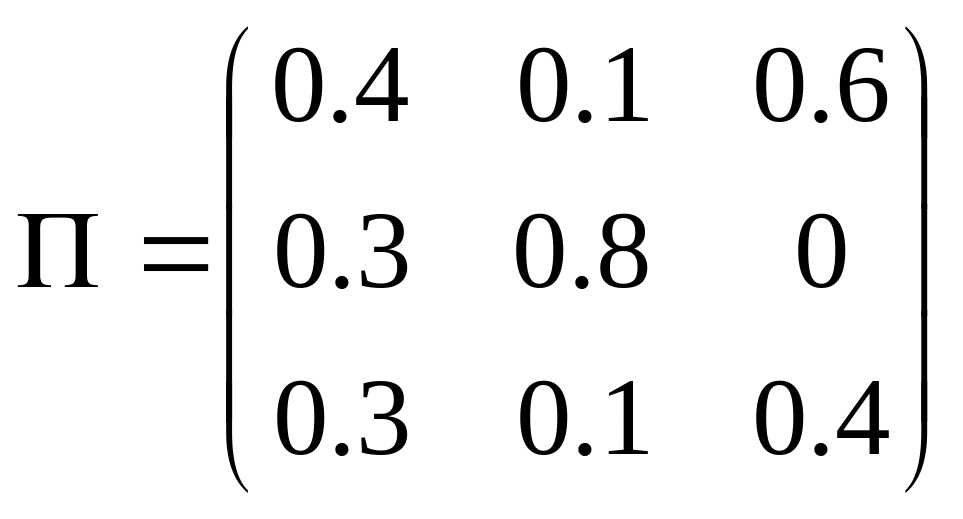
26.

27.

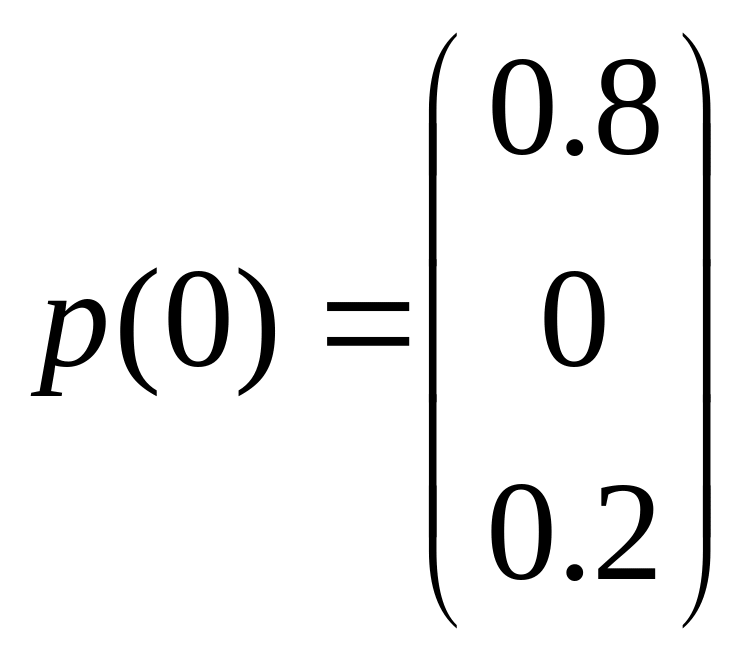
28.

29.

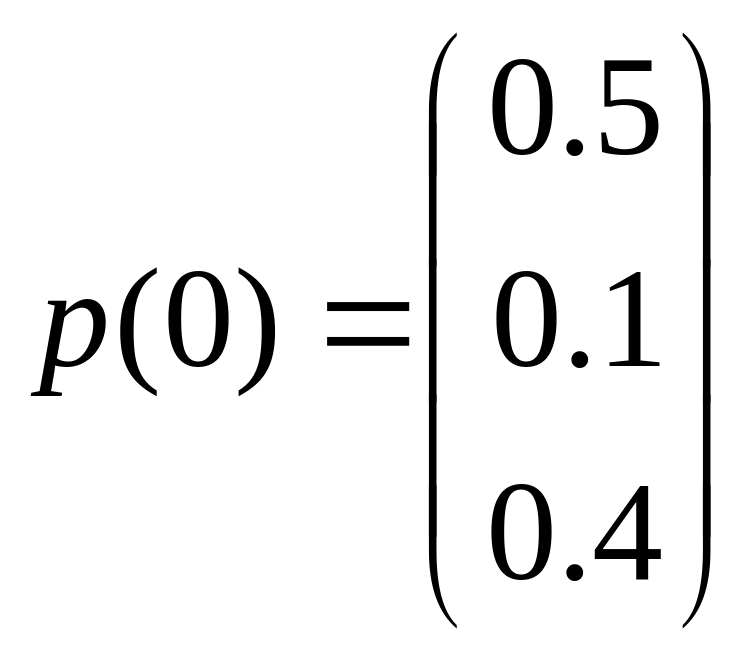
30.

Завдання № 3

Задано марковський процес з неперервним часом, трьома станами , , та інтенсивностями переходу , , , , , між цими станами. Знайти ймовірності , , перебування системи відповідно в станах , , у момент часу та граничний стан системи, якщо відомо, що в початковий момент часу система перебувала у стані .

№
1	1	5	6	3	4	1	1
2	2	1	9	1	4	3	2
3	5	5	1	7	1	6	3
4	2	3	3	5	7	2	1
5	3	2	6	2	6	4	2
6	1	3	2	4	2	7	3
7	3	1	2	5	7	3	1
8	2	3	1	3	4	5	2
9	1	`1	3	7	3	5	3
10	4	5	1	2	2	4	1
11	3	4	1	4	8	5	2
12	3	3	4	6	4	7	3
13	5	2	1	4	9	5	1
14	1	5	2	5	3	4	2
15	1	2	5	3	5	7	3
16	6	1	2	4	9	6	1
17	3	6	8	6	1	4	2
18	2	2	6	1	6	9	3
19	7	3	3	9	1	7	1
20	3	7	4	7	5	6	2
21	4	4	7	2	7	1	3
22	8	2	3	4	5	8	1
23	6	8	5	8	4	3	2
24	2	4	8	6	8	10	3
25	9	3	4	5	6	9	1
26	1	9	3	9	5	7	2
27	7	5	9	3	9	1	3
28	10	2	4	8	9	10	1
29	2	10	1	10	4	7	2
30	8	6	10	4	10	2	3

Завдання № 4

На телефонну станцію надходить пуассонівський потік інтенсивністю (викликів за хвилину). Знайти ймовірність наступних подій

1. у першу та другу хвилину на станцію надійде по одному виклику

2. за третю та четверту хвилини на станцію поступить разом три виклики

3. перший виклик на станцію прийде на другій хвилині

4. за першу і третю хвилини разом поступить не більше одного виклику

5. за перші дві хвилини на станцію поступить два виклики, за третю хвилину – один

6. за кожну з перших п’яти хвилин на стацію поступатиме по одному виклику

7. за сьому та восьму хвилини разом на станцію поступить не більше двох викликів

8. перший виклик на станцію надійде на третій хвилині

9. за перші шість хвилин на станцію не поступить жодного виклику

10. з сьомої по десяту хвилини на станцію поступатиме по два виклики

11. за перші чотири хвилини на станцію прийде не менше двох, але не більше трьох викликів

12. перший виклик поступить на станцію не раніше дев’ятої хвилини

13. за першу хвилину на станцію поступить один виклик, за наступні дві хвилини – ще два виклики

14. за перші вісім хвилин на станцію поступлять виклики, але не більше двох

15. за другу хвилину поступить лише другий за чергою виклик

16. за третю та четверту хвилину на станцію надійде по одному виклику

17. за другу та третю хвилини на станцію поступить разом три виклики

18. перший виклик на станцію прийде на третій хвилині

19. за першу і четветру хвилини разом поступить не більше одного виклику

20. за шосту та сьому хвилини на станцію поступить два виклик, за восьму хвилину – один

21. з восьмої по дванадцяту хвилини на стацію поступатиме по одному виклику

22. за десяту та одинадцяту хвилини разом на станцію поступить не більше двох викликів

23. перший виклик на станцію надійде на п’ятій хвилині

24. за перші шістнадцять хвилин на станцію на поступить жодного виклику

25. з одинадцятої по тринадцяту хвилини на станцію поступатиме по два виклики

26. за перші вісім хвилини на станцію прийде не менше одного, але не більше двох викликів

27. на протязі двох хвилин після першого виклику на станцію не поступатимуть виклики

28. за третю хвилину на станцію поступить один виклик, за наступні три хвилини – ще два виклики

29. за перші шість хвилин на станцію поступлять виклики, але не більше двох

30. на протязі хвилини після першого виклику на станцію поступить ще рівно один виклик.

Завдання № 5

На вхід лінійної динамічної системи, що задається рівнянням подається стаціонарний випадковий процес з математичним сподіванням та кореляційною функцією .

Для вхідного випадкового процесу ;