
- •1. Определители и их свойства.
- •2. Матрицы. Умножение матриц.
- •3. Обратная матрица.
- •Теорема условия существования обратной матрицы
- •Алгоритм нахождения обратной матрицы
- •4. Правило Крамера решения систем линейных уравнений.
- •5. Метод Гаусса решения систем линейных уравнений.
- •6. Системы координат.
- •Операция сложения двух векторов - правило треугольника.
- •8. Скалярное произведение векторов. Длина вектора.
- •11. Уравнение прямой с угловым коэффициентом.
- •12. Расстояние от точки до прямой.
- •13. Уравнение прямой, проходящей через две заданные точки.
- •14. Угол между двумя прямыми на плоскости.
- •15. Условия параллельности и перпендикулярности прямых.
- •16. Уравнения плоскости в пространстве.
- •17. Угол между плоскостями.
- •18. Уравнение прямой в пространстве.
- •19. Угол между прямыми в пространстве.
15. Условия параллельности и перпендикулярности прямых.
Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.
![]()
Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
![]()
16. Уравнения плоскости в пространстве.
Простейшей
поверхностью является плоскость.
Плоскость в пространстве
![]() можно
задать разными способами. Каждому из
них соответствует определенный вид
уравнения плоскости.
можно
задать разными способами. Каждому из
них соответствует определенный вид
уравнения плоскости.
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Найдем
уравнение плоскости, проходящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() ,
называемому нормалью к плоскости. Для
любой точки плоскости
вектор
,
называемому нормалью к плоскости. Для
любой точки плоскости
вектор
![]() ортогонален
(перпендикулярен) вектору
ортогонален
(перпендикулярен) вектору
![]() ,
следовательно, их скалярное произведение
равно нулю:
,
следовательно, их скалярное произведение
равно нулю:
![]() или
или
![]() .
.
Общее уравнение плоскости
После преобразования, уравнение
|
можно
записать в виде
Уравнение плоскости в отрезках Если же общее уравнение плоскости является полным
(т.е. ни один из коэффициентов не равен нулю), то его можно преобразовать к виду, называемому уравнением плоскости в отрезках
|
Уравнение плоскости, проходящей через три данные точки
Пусть
плоскость проходит через точки
![]() и
и
![]() ,
не лежащие на одной прямой и
–
произвольная точка плоскости. Тогда
векторы
,
не лежащие на одной прямой и
–
произвольная точка плоскости. Тогда
векторы
![]() ,
,
![]() ,
компланарны.
Следовательно, их смешанное произведение
равно нулю. Используя координатную
запись смешанного произведения, получаем:
,
компланарны.
Следовательно, их смешанное произведение
равно нулю. Используя координатную
запись смешанного произведения, получаем:
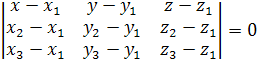 .
.
Это
уравнение, которому удовлетворяют
координаты
![]() любой
точки, лежащей на искомой плоскости,
является уравнением плоскости, проходящей
через три данные точки.
любой
точки, лежащей на искомой плоскости,
является уравнением плоскости, проходящей
через три данные точки.
Нормальное уравнение плоскости
Положение
плоскости
![]() вполне
определяется заданием единичного
вектора
вполне
определяется заданием единичного
вектора
![]() ,
имеющего направление перпендикуляра
,
имеющего направление перпендикуляра
![]() ,
опущенного на плоскость из начала
координат, и длиной p этого перпендикуляра
,
опущенного на плоскость из начала
координат, и длиной p этого перпендикуляра
Пусть
![]() ,
а
,
а
![]() –
углы, образованные единичным вектором
с
осями
–
углы, образованные единичным вектором
с
осями
![]() и
и
![]() ;
;
![]() Возьмем
на плоскости произвольную точку
Возьмем
на плоскости произвольную точку
![]() и
соединим ее с началом координат. Образуем
вектор
и
соединим ее с началом координат. Образуем
вектор
![]() .
При любом положении точки Μ на плоскости
проекция
радиус-вектора
.
При любом положении точки Μ на плоскости
проекция
радиус-вектора
![]() на
направление вектора
всегда
равно
на
направление вектора
всегда
равно
![]() :
:
![]() ,
т.е.
,
т.е.
![]() или
или
![]() –
нормальное уравнение плоскости в
векторной форме. Записав его в координатах
получим нормальное уравнение плоскости
в координатной форме:
–
нормальное уравнение плоскости в
векторной форме. Записав его в координатах
получим нормальное уравнение плоскости
в координатной форме:
![]() .
.
Общее уравнение плоскости можно привести к нормальному уравнению так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части общего уравнения на нормирующий множитель
![]()
где
знак берется противоположным знаку
свободного члена
![]() общего
уравнения плоскости.
общего
уравнения плоскости.

