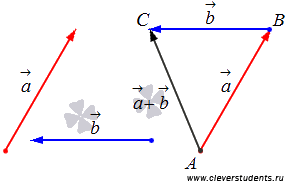
Операция сложения двух векторов - правило треугольника.

Сложение векторов и происходит так: от произвольной точки A откладывается вектор , равный , далее от точки B откладываеься вектор , равный , и вектор представляет собой сумму векторов и . Такой способ сложения двух векторов назвается правилом треугольника.

Проиллюстрируем сложение не коллинеарных векторов на плоскости по правилу треугольника.

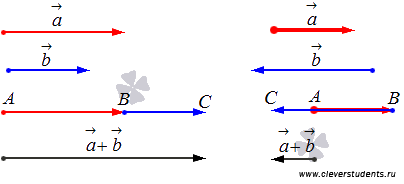
А на чертеже ниже показано сложение сонаправленных и противоположно направленных векторов.

Сложение нескольких векторов - правило многоугольника.

Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.

Сложение нескольких векторов выполняется следующим построением. От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B - это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор .

Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.

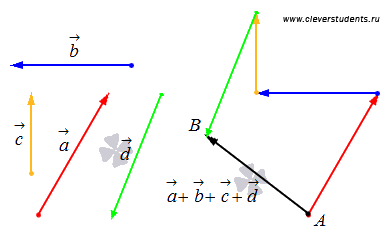
Абсолютно аналогично производится сложение нескольких векторов в пространстве.

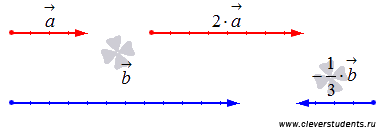
Операция умножения вектора на число.

Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор.

К примеру, при умножении вектора на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.

8. Скалярное произведение векторов. Длина вектора.

Определение.

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.

Скалярное произведение векторов и будем обозначать как . Тогда формула для вычисления скалярного произведения имеет вид 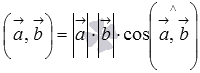, где и - длины векторов и соответственно, а 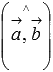- угол между векторами и .

Из определения скалярного произведения видно, что если хотя бы один из умножаемых векторов нулевой, то .

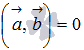Вектор можно скалярно умножить на себя. Скалярное произведение вектора на себя равно квадрату его длины, так как по определению .

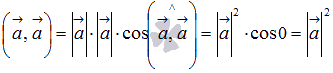Определение.

Скалярное произведение вектора на себя называется скалярным квадратом.

Формулу для вычисления скалярного произведения можно записать в виде , где - числовая проекция вектора на направление вектора , а - числовая проекция вектора на направление вектора .

Таким образом, можно дать еще одно определение скалярного произведения двух векторов.

Определение.

Скалярным произведением двух векторов и называется произведение длины вектора на числовую проекцию вектора на направление вектора или произведение длины вектора на числовую проекцию вектора на направление вектора .

Это определение эквивалентно первому.

Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль.

Длина вектора на плоскости вычисляется по следующей формуле:

Длина вектора в трехмерном пространстве вычисляется по следующей формуле:

Формула длины вектора в n-мерном пространстве:

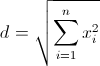
9. Угол между векторами. Условия параллельности и перпендикулярности.

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

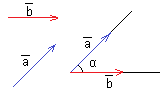
По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами обозначается так: . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).

  Условия параллельности и перпендикулярности векторов      Так как скалярное произведение двух перпендикулярных векторов  и  равно 0, то условием перпендикулярности отличных от нуля векторов будет равенство .      При умножении вектора  на скаляр  получаем вектор  одного направления с  при λ > 0и противоположного направления при λ < 0. Но всегда векторы  будут параллельны.      Поэтому условием параллельности векторов  будет пропорциональность их соответствующих координат: .

10. Общее уравнение прямой.

Общие уравнения прямой

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Прямую в пространстве невозможно задать одним уравнением. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой. Для этого требуется система двух или более уравнений.

Пусть две плоскости  и  заданы общими уравнениями вида  и , т.к. коэффициенты  и  не пропорциональны, то плоскости не параллельные. Тогда прямая в пространстве есть пересечение этих плоскостей:

 

 

Эти уравнения называются общими уравнениями прямой.

Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.

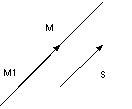
Уравнения прямой, проходящей через точку параллельно вектору (канонические уравнения прямой)

Пусть прямая проходит через точку  параллельно вектору . Так как любой ненулевой вектор, параллельный данной прямой, является ее направляющим вектором, то для любой точки , лежащей на данной прямой, вектор  коллинеарен направляющему вектору . Поэтому их соответствующие координаты должны быть пропорциональны, следовательно, имеют место равенства: ,

 

называемые каноническими уравнениями  прямой в пространстве.

Уравнения прямой, проходящей через две данные точки

Пусть прямая проходит через две точки: , направ­ляющим вектором такой прямой является вектор , и уравнения  принимают вид:

 

 

 уравнения прямой, проходящей через две данные точки.

 

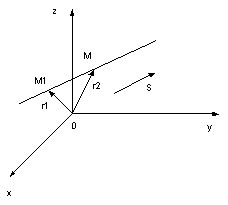
Векторное уравнение прямой. Параметрические уравнения прямой

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки  и направляющего вектора , параллельного этой прямой.

Пусть прямая проходит через точку , лежащую на прямой параллельно вектору . Рассмотрим произвольную точку  на прямой. Очевидно, что . Так как векторы  и  коллинеарны, то найдется такое число , что , причем число  может принимать любое числовое значение в зависимости от положения точки  на прямой. Множитель  называется параметром. Обозначив радиус-векторы точек  и  соответственно через  и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра  соответствует радиус-вектор некоторой точки , лежащей на прямой.

Так как векторы      то

.

 

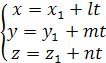Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра  изменяются координаты и  и точка  перемещается по прямой.

Замечание. Если принять каждую из равных дробей в канонических уравнениях прямой  за некоторый параметр , , то можно получить параметрические уравнения .