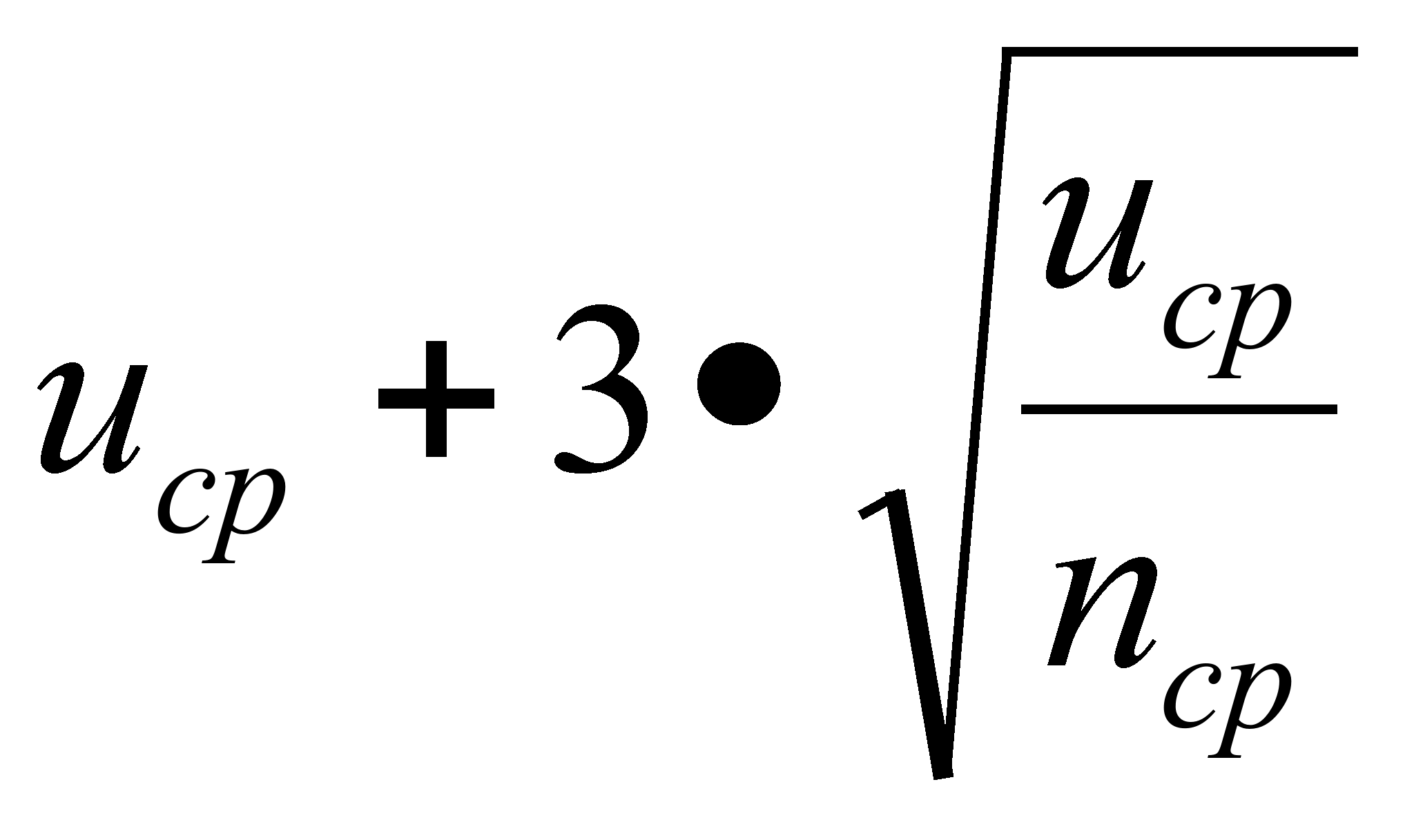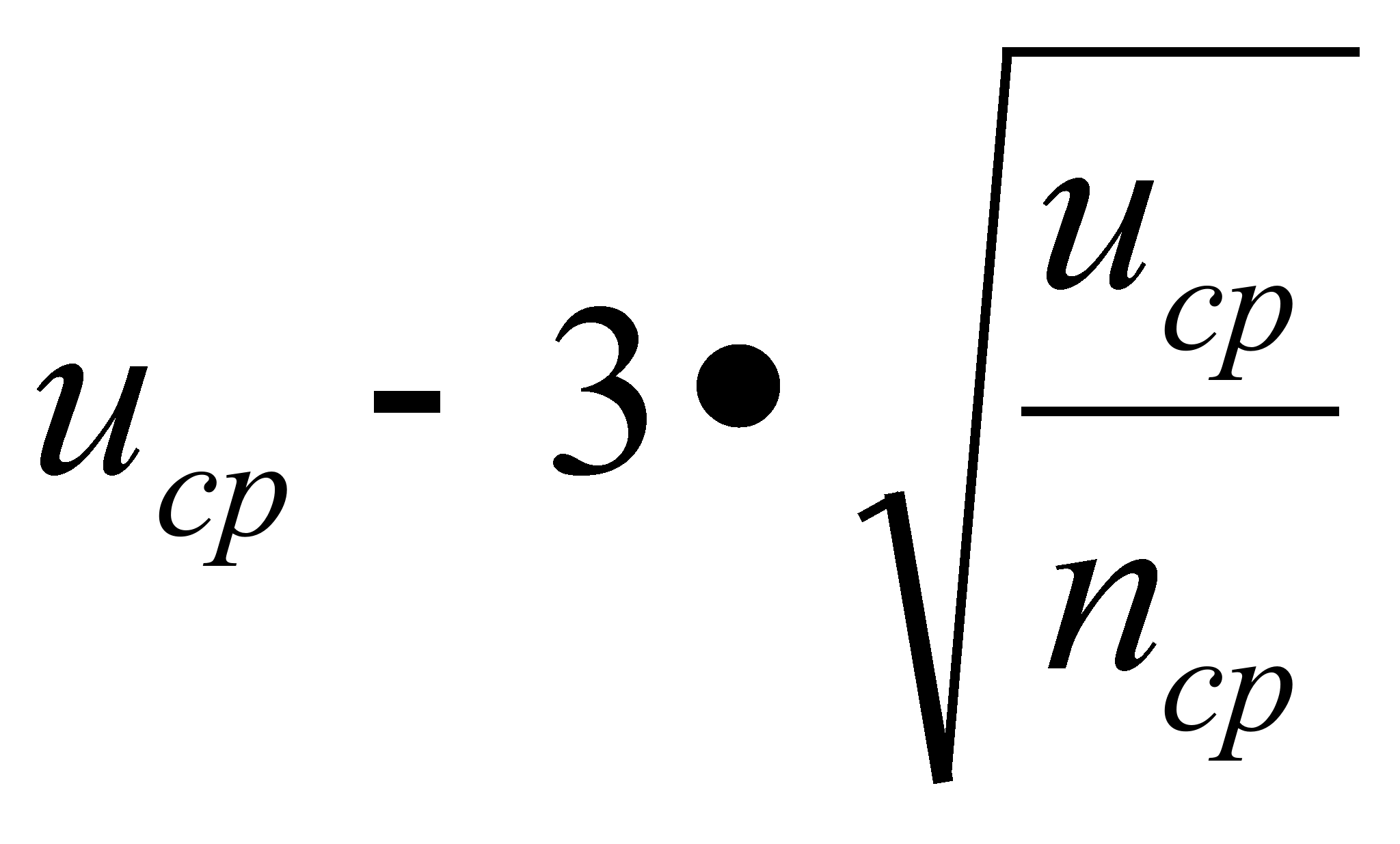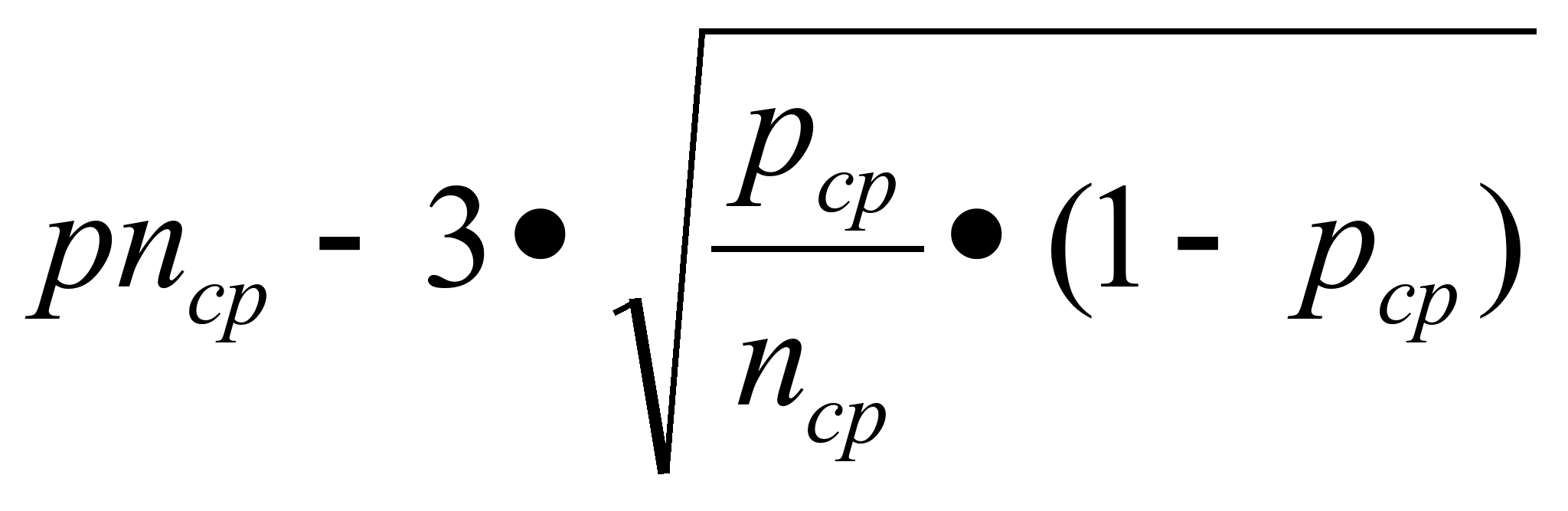Карты кумулятивных сумм

Общепринятая методология построения контрольных карт имеет ту особенность, что проводимый контроль не учитывает предыдущего поведения контролируемого параметра. Гораздо лучшие результаты дает методика, учитывающая для анализа текущего состояния информацию о прошлых данных. В основе этой методики лежит исследование не индивидуальных значений признака качества, а учет их кумулятивных сумм. Такой подход получил название метода кусумм (или кусумм-метода).

Если есть ряд значений признака x₁, x₂, ..., то образование кусумм будет происходить следующим образом:

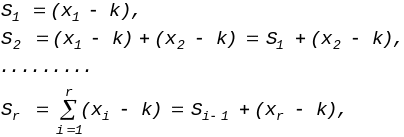(1.38)

где k — константа, представляющая собой некоторое эталонное значение.

Вычисленные и нанесенные на график в порядке появления кумулятивные суммы (S_r) образуют кусумм-карту.

Константа k может принимать любое значение, даже нулевое, одноко для того, чтобы карта имела компактный вид и умещалась на обычном листе бумаги, величину k, приравнивают чаще всего точно или приблизительно к математическому ожиданию. Это удобно еще и потому, что константа k оказывается тогда близкой к номиналу параметра процесса.

Если среднее значение параметра процесса возрастает, то будет иметь место и общий рост уровня кусуммы, поскольку все большее число значений (x_i-k) станут положительными. Аналогичным образом, если среднее значение будет падать, то и график будет стремиться вниз.

Действительно, изменение среднего значения исходных данных приводит к изменению угла наклона графика кусумм. Фактическая величина кумуммы в отдельной точке не имеет никакого значения. Из-за мелких случайных колебаний параметров процесса на отдельных участках графика могут проявляться различные тенденции в угле наклона. И только построение среднего наклона графика позволяет установить, имели ли место какие-либо изменения.

Преимущество карт кусумм перед обычными контрольными картами еще и в том, что они создают основу для управления, когда лишь доступны индивидуальные значения (т.е. объем выборки n=1). Это обстоятельство делает метод кусумм идеальным средством управления процессами с относительно низким уровнем производительности или высокой стоимостью измерений.

Статистические методы играют важную роль в объективной оценке количественных и качественных характеристик процесса и являются одним из важнейших элементов системы обеспечения качества продукции и всего процесса управления качеством. Неслучайно основоположник современной теории менеджмента качества Э. Деминг много лет работал в Бюро по переписи населения и занимался именно вопросами статистической обработки данных. Он придавал огромное значение статистическим методам.

Для получения качественной продукции необходимо знать реальную точность имеющегося оборудования, определять соответствие точности выбранного технологического процесса заданной точности изделия, оценивать стабильность технологического процесса. Решение задач указанного типа производится в основном путем математической обработки эмпирических данных, полученных многократными измерениями либо действительных размеров изделий, либо погрешностей обработки или погрешностей измерения.

Существуют две категории погрешностей: систематические и cлучайные. В результате непосредственных наблюдений, измерений или регистрации фактов получается множество данных, которые образуют статистическую совокупность и нуждаются в обработке, включающей систематизацию и классификацию, расчет параметров, характеризующих эту совокупность, составление таблиц, графиков, иллюстрирующих процесс.

На практике используют ограниченное количество числовых характеристик, называемых параметрами распределения.

Центр группирования. Одной из основных характеристик статистической совокупности, дающей представление о том, вокруг какого центра группируются все значения, является среднее арифметическое. Оно определяется из выражения:

(1)

где Хi — измеренный параметр i-го члена совокупности, n — количество членов совокупности.

Величина рассеяния. Статические совокупности могут иметь близкие или даже одинаковые значения центра группирования, но отдельные значения величин в них могут существенно отличаться, вследствие того, что разброс значений относительно центра бывает разный. Самой элементарной характеристикой рассеяния является вариационный размах R, определяемый по формуле

R = Xmax — Xmin

(2)

где Xmax, Xmin — максимальное и минимальное значения статистической совокупности.

Вариационный размах не всегда характерен, так как учитывает только крайние значения, которые могут сильно отличаться от всех других значений. Более точно рассеяние определяется с помощью показателей, учитывающих отклонение всех значений от среднего арифметического. Основным из этих показателей является среднее квадратичное отклонение результата наблюдений, которое определяется по формуле

(3)

Это отклонение является наиболее распространенным и общепринятым показателем вариации. Величина под корнем, то есть σ², называется дисперсией. Дисперсия имеет самостоятельное значение во многих задачах математической статистики и относится к числу важнейших показателей вариации.

Показателем отклонения значения самого среднего арифметического является среднее квадратическое отклонение среднего значения S, которое еще называют среднее квадратическое отклонение результата измерения.

(4)

Форма распределения вероятности. Для характеристики формы распределения обычно используют ту математическую модель, которая наилучшим образом приближает к виду кривой распределения вероятностей, полученной при анализе экспериментально полученных данных.

Закон нормального распределения. Большинство случайных явлений, происходящих в жизни, в частности, в производстве и научных исследованиях, характеризуются наличием большого числа случайных факторов, описывается законом нормального распределения, который является основным во многих практических исследованиях. Однако нормальное распределение не является единственно возможным. В зависимости от физической природы случайных величин, некоторые из них на практике могут иметь распределение другого вида, например, логарифмическое, экспоненциальное, Вейбулла, Симпсона, Релея, равной вероятности и др.

Уравнение, описывающие плотность вероятности нормального распределения имеет вид:

(5)

Нормальное распределение характеризуется двумя параметрами μ и σ² и на графике представляет собой симметричную кривую Гаусса (рисунок 1), имеющую максимум в точке соответствующей значению Х = μ (соответствует среднему арифметическому Х_ср и называется центром группирования), а при Х → -∞ и Х → ∞ асимптотически приближающуюся к оси абсцисс. Точка перегиба кривой находится на расстоянии σ от центра расположения μ. С уменьшением σ кривая растягивается вдоль оси ординат и сжимается вдоль оси абсцисс. Между абсциссами μ — σ и μ + σ расположено 68,3 % всей площади кривой нормального распределения. Это означает, что при нормальном распределении 68,3 % всех измеренных единиц отклоняются от среднего значения не более чем на σ, то есть все они находятся в пределах + σ. Площадь, заключенная между ординатами, проведенными на расстоянии 2σ с обеих сторон от центра составляет 95,4 % и соответственно столько же единиц совокупности находится в пределах μ+2σ. И наконец, 99,73 % всех единиц находится в пределах μ+3σ. Это так называемое правило «трех сигм», характерное для нормального распределения. Согласно этому правилу за пределами отклонения на 3σ находится не более 0,27 % всех значений величин, то есть 27 реализаций на 10 тысяч. В технических приложениях принято при оценке результатов измерений работать с коэффициентами z при σ, соответствующим 90 %, 95 %, 99 %, 99,9 % вероятности попадания результата в область допуска.

  Рисунок 1

Z90 = 1,65; Z95 = 1,96; Z99 = 2,576; Z999 = 3,291.

Следует отметить, что это же правило распространяется на отклонения среднего значения Х_ср(?). Оно также колеблется в некоторой области на три значения среднего квадратического отклонения среднего значения S в обе стороны, и в этой области заключено 99,73 % всех значений среднего значения. Нормальное распределение хорошо проявляется при большом количестве членов статистической совокупности, не менее 30.

Распределение Стьюдента. Для практики большой интерес представляет возможность судить о распределении случайных величин и определять производственные погрешности во всех изготовленных изделиях и погрешности научных экспериментов по результатам измерения параметров статистической совокупности полученным из партии малого объема. Эта методика была разработана Карлом Госсетом в 1908 году и опубликована под псевдонимом Стьюдент.

Распределение Стьюдента симметрично, но более сплющено, чем кривая нормального распределения, и поэтому вытянуто на концах (рисунок 2). Для каждого значения n имеется своя t-функция и свое распределение. Коэффициент z заменен в распределении Стьюдента коэффициентом t, значение которого зависит от заданного уровня значимости, который определяет какая часть реализации может находиться за пределами выбранной области кривой распределения Стьюдента и количества изделий в выборке.

  Рисунок 2

При больших n распределение Стьюдента асимптотически сближается со стандартным нормальным распределением. С приемлемой для практики точностью можно считать, что при n?30, распределение Стьюдента, которое иногда называют t-распределением, апроксимируется нормальным.

t-распределение имеет те же самые параметры, что и нормальное. Это среднее арифметическое Хср , среднее квадратическое отклонение ? и среднее квадратическое отклонение среднего S. Хср определяется по формуле (1), S определяется по формуле (4), а ? по формуле:

(6)

Контроль точности. Когда известно распределение случайной величины, можно получить все особенности данной партии изделий, определить среднее значение, дисперсию и т.п. Но полная совокупность статистических данных партии промышленных изделий, а значит закон распределения вероятностей смогут быть известными, только после изготовления всей партии изделий. На практике закон распределения всей совокупности изделий почти всегда неизвестен, единственным источником информации служит выборка, обычно малая. Каждая рассчитанная по выборочным данным числовая характеристика, например, среднее арифметическое или дисперсия есть реализация случайной величины, которая от выборки к выборке может принимать различные значения. Задача контроля облегчается благодаря тому, что обычно не требуется знать точного значения отличий случайных значений от заданной величины. Достаточно лишь знать отличаются ли наблюдаемые значения больше чем на величину допускаемой ошибки, которая определяется величиной допуска. Распространение на генеральную совокупность оценок, сделанных по выборочным данным, может быть осуществлено только с некоторой вероятностью Р(t). Таким образом, суждение о свойствах генеральной совокупности всегда носит вероятностный характер и содержит элемент риска. Так как заключение делается по выборочным данным, то есть при ограниченном объеме информации, могут возникать ошибки первого и второго рода.

Вероятность допустить ошибку первого рода называют уровнем значимости и обозначают а. Область, отвечающая вероятности а, называется критической, а дополняющая ее область, вероятность попадания в которую равна 1-а, называется допустимой.

Вероятность ошибки второго рода обозначается ?, а величина 1-? называется мощностью критерия.

Величина а иногда называется риском изготовителя, а величина ? называется риском потребителя.

С вероятностью 1-а неизвестное значение Х₀ полной совокупности лежит в интервале

(Хср — Z?) < Х₀< (Хср + Z?) для нормального распределения,

(Хср — t?) < Х₀< (Хср + t?) для распределения Стьюдента.

Предельные крайние значения Х₀ называют доверительными границами.

При уменьшении объема выборки при распределении Стьюдента доверительные границы расширяются, а вероятность ошибки возрастает. Задаваясь, например, 5% уровнем значимости (а=0,05), считают, что с вероятностью 95% (Р=0,95) неизвестное значение Х₀ находится в интервале

(Хср — t?,:., Хср+t?)

Иными словами искомая точность будет равна Хср+t?, причем количество деталей с размером, выходящим за пределы этого допуска, будет составлять не более 5 %.

Контроль стабильности процесса. В реальных условиях производства фактические значения параметров технологического процесса и характеристик изготовляемой продукции не только хаотично изменяются за счет случайных погрешностей, но часто с течением времени постепенно и монотонно отклоняются от заданных значений, то есть имеет место появление систематических погрешностей. Эти погрешности должны ликвидироваться путем выявления и устранения вызывающих их причин. Проблема заключается в том, что в реальных условиях систематические погрешности трудно отличить от случайных. Незначительные систематические погрешности без специального статистического анализа могут долго оставаться незамеченными на фоне случайных погрешностей.

Анализ основан на том, что когда систематические ошибки отсутствуют, фактические значения параметров изменяются случайным образом. Однако их средние значения и основные ошибки остаются неизменными во времени. В таком случае технологический процесс называют стабильным. Условно считается, что в данной партии все изделия являются одинаковыми. При стабильном процессе случайные погрешности подчиняются нормальному закону распределения с центром μ=Хо. Среднее значения параметров, полученные в различных партиях, должны быть приближенно равны Хо. Следовательно, все они приближенно равны между собой, но величина текущего среднего значения Хсрт колеблется в доверительном интервале+tS, то есть:

(Хср — tS) ≤ Хсрт ≤ (Хср + tS)

(7)

Материалом для анализа стабильности могут служить те же данные, которые использовались для контроля точности. Но они будут пригодны лишь в том случае, если представляют собой непрерывные наблюдения, охватывающие достаточный промежуток времени, или если они составлены из выборок, отобраны через определенные промежутки времени. Интервалы между выборками, называемые в этом случае пробами, устанавливают в зависимости от наблюдаемой частоты разладок оборудования.

При заданном уровне значимости среднее значение Хсрт в различных текущих партиях могут различаться не более чем на величину tS от базового Хср, полученного для первого замера, то есть

/Хср — Хсрт/ ≤ tS

(8)

При выполнении этого условия можно считать, что процесс стабилен и обе партии выпущены при одинаковых условиях. Если же различие средних значений в двух партиях будет превосходить величину tS, то уже нельзя считать, что это различие вызвано только случайными причинами. В процессе появился доминирующий постоянный фактор, который изменяет значения параметров изделий в партии по определенному постоянному закону. Процесс является нестабильным и изделия, выпускаемые в разное время, будут значительно отличаться друг от друга, причем эта разница будет увеличиваться со временем.

Таким образом, расхождение средних значений в различных партиях больше чем на tS, указывает на наличие систематических ошибок и на необходимость принятия мер для их обнаружения и устранения причин, которые их вызывают. Этот принцип был применен В. Шухартом при разработкеконтрольных карт.

Статистические методы анализа стабильности могут применяться также в ситуациях, противоположных рассмотренным выше. Если в конструкцию изделия или технологический процесс его изготовления вносят какие-то изменения, то требуется определить, в какой мере это приведет к ожидаемым результатам.

Следовательно, требуется провести испытания, сделать несколько проб и статистически обработать данные. Если

/Хср.ст.-Хср.нов./ > tS,

(9)

то эффект усовершенствования можно считать значимым.

Семь простейших методов статистического исследования процесса

Современные статистические методы довольно сложны для восприятия и широкого практического использования без углубленной математической подготовки всех участников процесса. К 1979 году Союз японских ученых и инженеров (JUSE) собрал воедино семь достаточно простых в использовании наглядных методов анализа процессов. При всей своей простоте они сохраняют связь со статистикой и дают профессионалам возможность пользоваться их результатами, а при необходимости — совершенствовать их.

Причинно-следственная диаграмма Исикавы. Данная диаграмма является очень мощным инструментом для анализа ситуации, получения информации и влиянии разных факторов на основной процесс. Здесь появляется возможность не только выявить факторы, влияющие на процесс, но и определить и приоритетность их влияния.

Рисунок 3

Диаграмма типа 5М рассматривает такие компоненты качества, как «люди», «оборудование», «материал, сырье», «технология», «управление», а в диаграмме типа 6М к ним добавляется компонент «среда» (рисунок 3).

Применительно к решаемой задаче квалиметрического анализа,

- для компоненты «люди» необходимо определить факторы, связанные с удобством и безопасностью выполнения операций;

- для компоненты «оборудование» — взаимоотношения элементов конструкции анализируемого изделия между собой, связанные с выполнением данной операции;

- для компоненты «технология» — факторы, связанные с производительностью и точностью выполняемой операции;

- для компоненты «материал» — факторы, связанные с отсутствием изменений свойств материалов изделия в процессе выполнения данной операции;

- для компоненты «технология» — факторы, связанные с достоверным распознаванием ошибки процесса выполнения операции;

- для компоненты «среда» — факторы, связанные с воздействием среды на изделие и изделия на среду.

Типы дефектов	Данные контроля	Итого
Вмятины	///// ///// ////	14
Трещины	///// ///// ///// //	17
Выход за допуск в минус	///// //	7
Выход за допуск в плюс	///// ///// ///// ///// ///	23
Прожиг при термообработке	///// ////	9
Перекос базовых поверхностей	///	3
Литейные раковины	///// /	6
Несоответствие шероховатости	///// ///// ///// ///	18
Дефекты покраски	////	4
Прочие	///// //	7
Итого		108

Рисунок 4

Контрольные листки. Контрольные листки могут применяться как при контроле по качественным, так и при контроле по количественным признакам, в этом документе фиксируются определенные виды дефектов за определенный отрезок времени. Контрольный листок является хорошим статистическим материалом для дальнейшего анализа и изучения проблем производства и уменьшения уровня дефектности (рисунок 4).

Анализ Парето. Анализ Парето получил свое название по имени итальянского экономиста Вилфредо Парето (1848-1923), который показал, что большая часть капитала (80%) находится в руках незначительного количества людей (20%). Парето разработал логарифмические математические модели, описывающие это неоднородное распределение, а математик М.О. Лоренц представил графические иллюстрации, в частности кумулятивную кривую.

Правило Парето — «универсальный» принцип, который применим во множестве ситуаций, и без сомнения — в решении проблем качества. Д. Джуран отметил «универсальное» применение принципа Парето к любой группе причин, вызывающих то или иное последствие, причем большая часть последствий вызвана малым количеством причин. Анализ Парето ранжирует отдельные области по значимости или важности и призывает выявить и в первую очередь устранить те причины, которые вызывают наибольшее количество проблем (несоответствий).

№№	1	2	3	4	5	6	7	8	9	10
Кол-во дефектов	23	18	17	14	9	7	7	6	4	3
Сумма дефектов	23 (21%)	41 (38%)	58 (54%)	72 (67%)	81 (75%)	88 (81%)	95 (88%)	101 (94%)	105 (97%)	108 (100%)

Рисунок 5

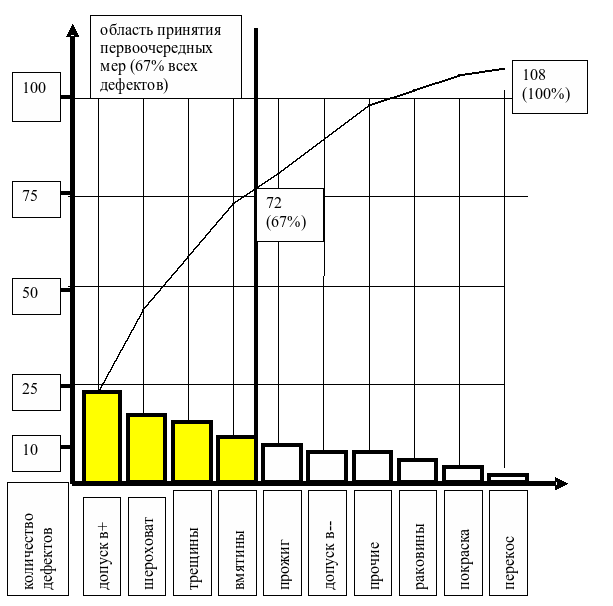
Анализ Парето, как правило, иллюстрируется диаграммой Парето (рисунок 5), на которой по оси абсцисс отложены причины возникновения проблем качества в порядке убывания вызванных ими проблем, а по оси ординат — в количественном выражении сами проблемы, причем как в численном, так и в накопленном (кумулятивном) процентном выражении. Построим диаграмму по данным, взятым из предыдущего примера — контрольного листка.

На диаграмме отчетливо видна область принятия первоочередных мер, очерчивающая те причины, которые вызывают наибольшее количество ошибок. Таким образом, в первую очередь, предупредительные мероприятия должны быть направлены на решение именно этих проблем. Выявление и устранение причин, вызывающих появление наибольшего количества дефектов, позволяет нам расходуя минимальное количество ресурсов (деньги, время, люди, материальное обеспечение) получить максимальный эффект в виде значительного уменьшения количества дефектов.

Стратификация. В основном, стратификация — процесс сортировки данных согласно некоторым критериям или переменным, результаты которого часто показываются в виде диаграмм и графиков. Мы можем классифицировать массив данных в различные группы (или категории) с общими характеристиками, называемыми переменной стратификации. Важно установить, которые переменные будут использоваться для сортировки. Стратификация — основа для других инструментов, таких как анализ Парето или диаграммы рассеивания. Такое сочетание инструментов делает их более мощными.

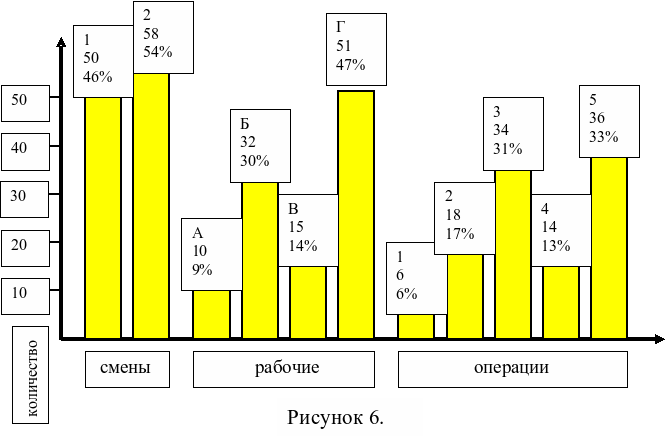
Возьмем данные из контрольного листка (рисунок 4). На рисунке 6 приведен пример анализа источника возникновения дефектов. Все дефекты 108 (100%) были классифицированы на 3 категории — по сменам, по рабочим и по операциям. Из анализа представленных данных наглядно видно, что наибольший вклад в наличие дефектов вносит 2 смена (54%) и рабочий Г (47%), который работает в этой смене.

Гистограммы. Гистограммы — один из вариантов столбчатой диаграммы, отображающий зависимость частоты попадания параметров качества изделия или процесса в определенный интервал значений от этих значений.

Внизу приведен пример построения гистограммы.

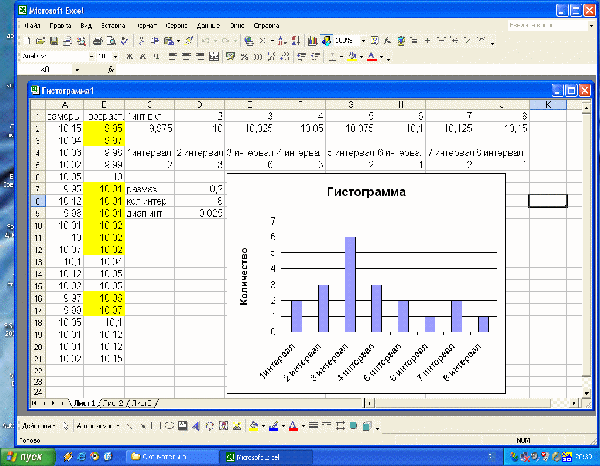
Для удобства расчетов и построения применяем прикладной компьютерный программный пакет EXCEL. Необходимо определить разброс значений геометрического размера, например, диаметр вала, номинальный размер которого равен 10 мм. Произведен замер 20 валов, данные замеров приведены в первом столбце А (рисунок 7). В столбце В производим расстановку замеров по возрастанию, затем в ячейке D7 определяем размах размеров, как разницу самого большого и малого значений замера. Выбираем количество интервалов гистограммы равным 8. Определяем диапазон интервала D. Затем определяем параметры интервалов, это наименьшее и наибольшее включительно значение геометрического параметра, входящего в интервал.

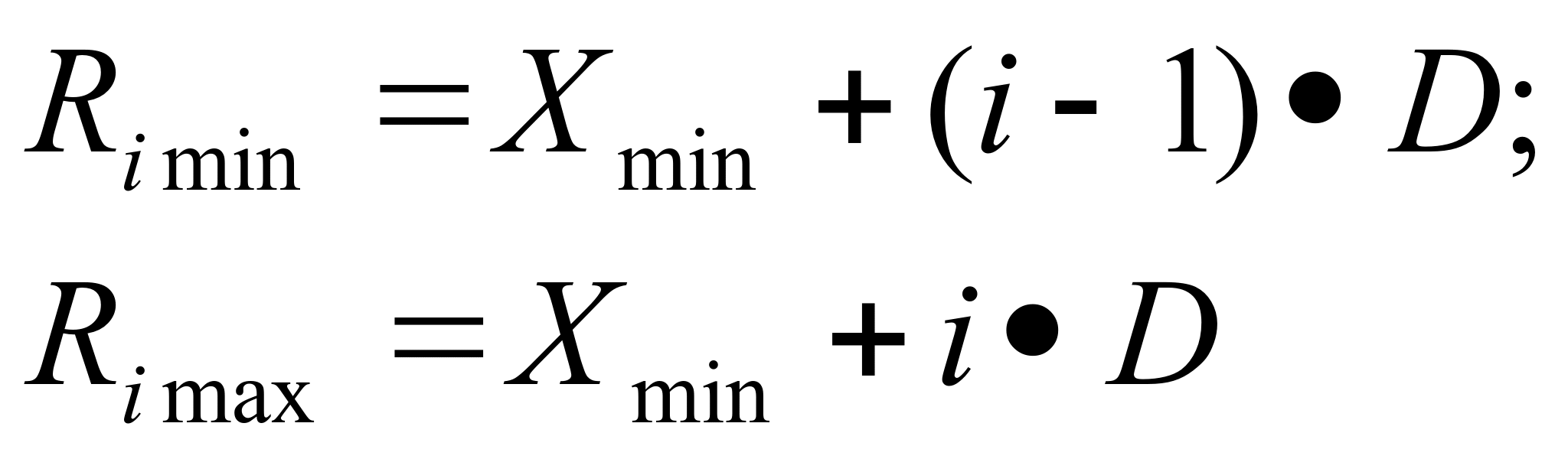
где i — номер интервала.

После этого определяем количество попаданий значений параметра в каждый из 8 интервалов, после этого окончательно строим гистограмму.

  Рисунок 7

Диаграммы разброса. Диаграммы разброса представляют из себя графики, которые позволяют выявить корреляцию (статистическую зависимость) между различными факторами, влияющими на показатели качества. Диаграмма строится по двум координатным осям, по оси абсцисс откладывается значение изменяемого параметра, а на оси ординат откладывается получаемое значение исследуемого параметра, которое мы имеем в момент использование изменяемого параметра, на пересечении этих значений ставим точку. Собрав достаточно большое количество таких точек, мы можем делать анализ и вывод.

Приведем пример. На предприятии решили проводить занятия по основам менеджмента качества. Каждый месяц обучение проходило определенное количество рабочих. В январе обучение прошли 2 человека, в феврале 3 человека и т.д. В течение года количество обученных работников возрастало и к концу года достигло 40 человек. Руководство дало поручение службе качества отследить зависимость процента бездефектной продукции, предъявляемой с первого раза, количества поступающих на завод рекламаций на продукцию со стороны заказчиков и расхода электроэнергии в цеху от количества обученных рабочих. Была составлена таблица 1 данных по месяцам и построены диаграммы разброса (рисунок 8, 9, 10). На них хорошо видно, что процент бездефектности повышается, имеем прямую корреляционную зависимость, количество рекламаций уменьшается, имеем обратную корреляционную зависимость, причем на диаграммах хорошо видна четко выраженная корреляционная зависимость, которая определяется по кучности точек и их приближении к какой либо точно очерченной траектории, в нашем случае это прямая линия. Количество расходуемой электроэнергии не имеет зависимости от количества обученных работников.

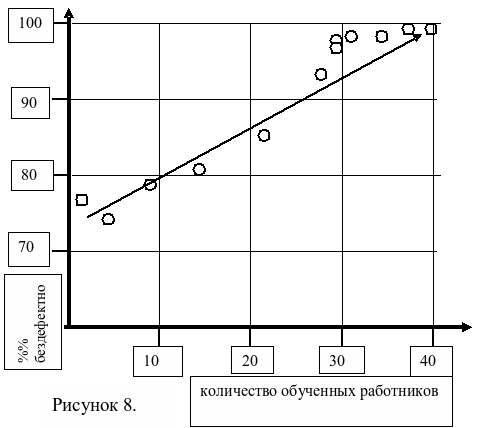
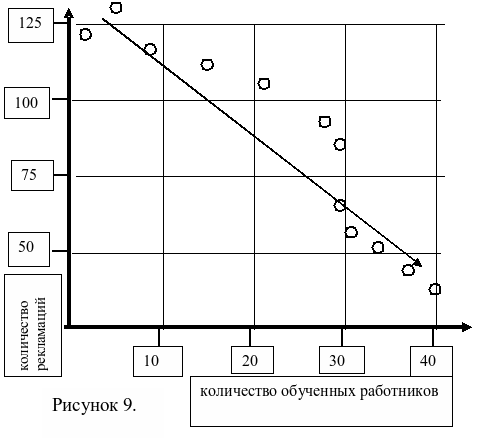
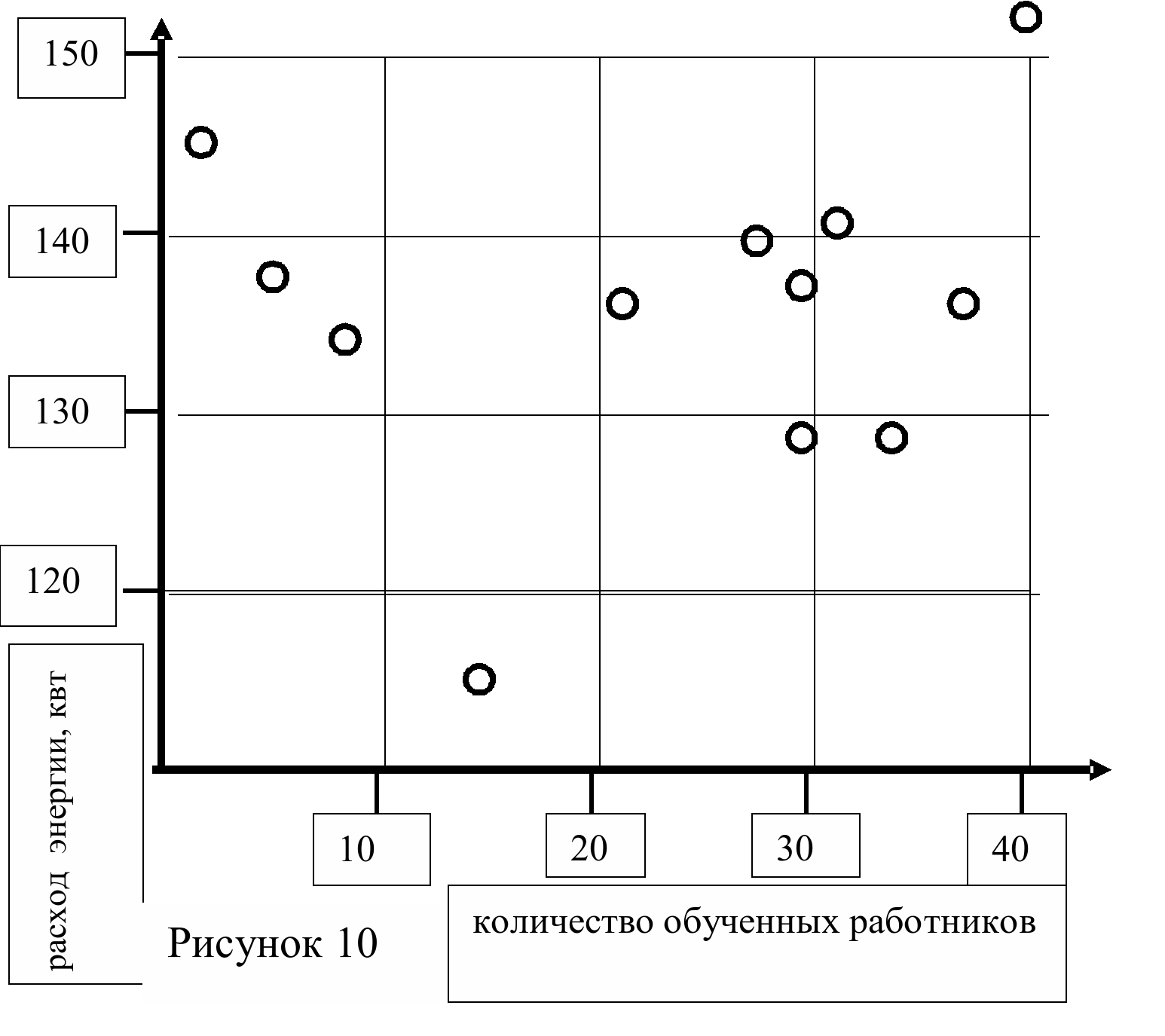
Таблица 1.

	Кол-во обученных рабочих	% бездефектности	Количество рекламаций	Расход энергии, кВт
январь	2	77	124	146
февраль	5	74	136	138
март	9	78	120	134
апрель	15	81	115	115
май	22	85	110	136
июнь	26	93	90	140
июль	28	95	82	137
август	28	96	63	129
сентябрь	29	98	59	141
октябрь	33	98	51	129
ноябрь	35	99	45	137
декабрь	40	99	38	153

Контрольные карты. Контрольные карты — специальный вид диаграммы, впервые предложенный В. Шухартом в 1924 г. Они отображают характер изменения показателя качества во времени, например, стабильности получения размера изделия. По существу контрольные карты показывают стабильность технологического процесса, то есть нахождение среднего значения параметра в коридоре допускаемых значений, состоящего из верхней и нижней границы допуска. Данные этих карт могут сигнализировать о том, что параметр приближается к границе допуска и необходимо уже принимать упреждающие действия еще до того как параметр выйдет в зону брака, то есть такой метод контроля позволяет предупреждать появление брака еще на стадии его зарождения.

Существуют 7 основных типов карт.

1. Отклонения среднеквадратического отклонения среднего значения х-S,

2. Отклонений размахов х-R,

3. Отклонений индивидуальных значений х,

4. Колебания числа дефектов С,

5. Колебания числа дефектов на единицу продукции u,

6. Колебания числа дефектных единиц продукции pn,

7. Колебания доли дефектной продукции p.

Все карты можно разбить на две группы. Первая контролирует количественные параметры качества, представляющие собой непрерывные случайные величины — размеры, масса и т.д. Вторая для контроля качественных альтернативных дискретных параметров (есть дефект — нет дефекта).

Таблица 2

Карты количественные			Карты качественные
			Число дефектов в выборке			Число дефектных изделий
x-S	x-R	x		C	u		pn	p
n большое	n малое	n=1		n постоянное	n разное		n постоянное	n разное

В таблице 3 приведены значения среднего параметра и верхней и нижней границ допуска.

Таблица 3

Карта	Среднее	Верхняя граница	Нижняя граница
x-S	Хср	Хср+tS	Хср-tS
x-R	Rcp
x	Xcp Rcp
C	Ccp
u	ucp
pn	рср
p	рср

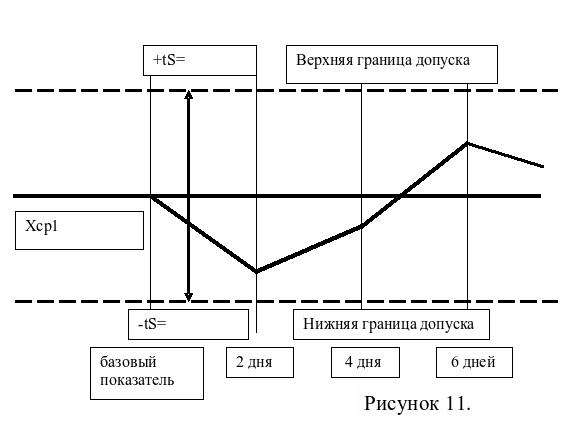
Например карта х-S. Колебания среднего арифметического значения, коридор допуска здесь является величина 3S (для нормального распределения) или tS (для распределения Стьюдента), где S — среднеквадратическое отклонение среднего. Середина коридора среднее арифметическое значение первого замера. Значения этой карты наиболее достоверны и объективны. Общий вид контрольной карты показан на рисунке 11.