1.3.Обратная матрица

Квадратные матрицы вида 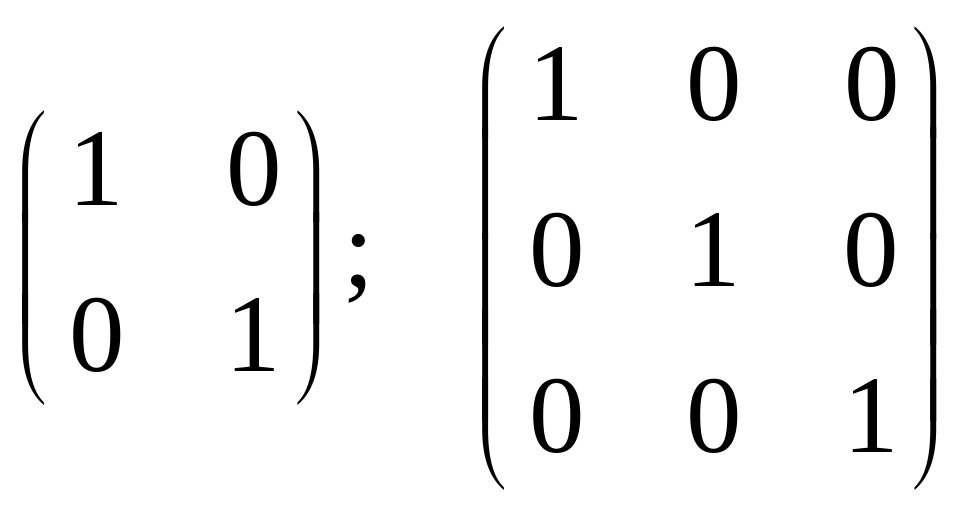(на главной диагонали единицы остальные нули) называются единичными и обозначаются через Е. Для любой квадратной матрицы А справедливы равенства АЕ=ЕА=А.

Если для квадратной матрицы, А определитель , то существует обратная матрица , для которой должны выполняться равенства

В случае матрицы размерами обратная матрица вычисляется по формуле

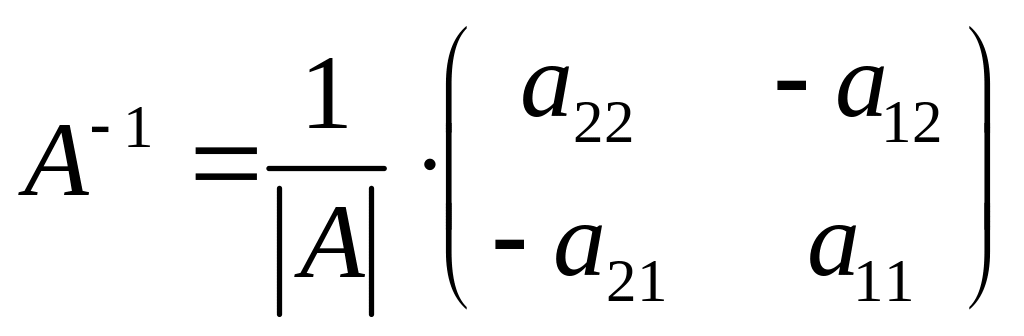
Пример. Найти обратную матрицу для матрицы

Решение. Найдем Тогда

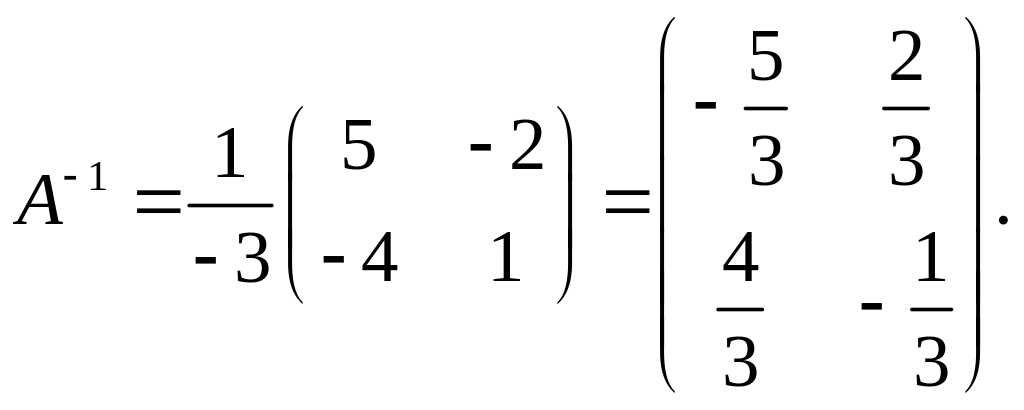
1.4.Системы линейных уравнений.

Система линейных уравнений имеет вид

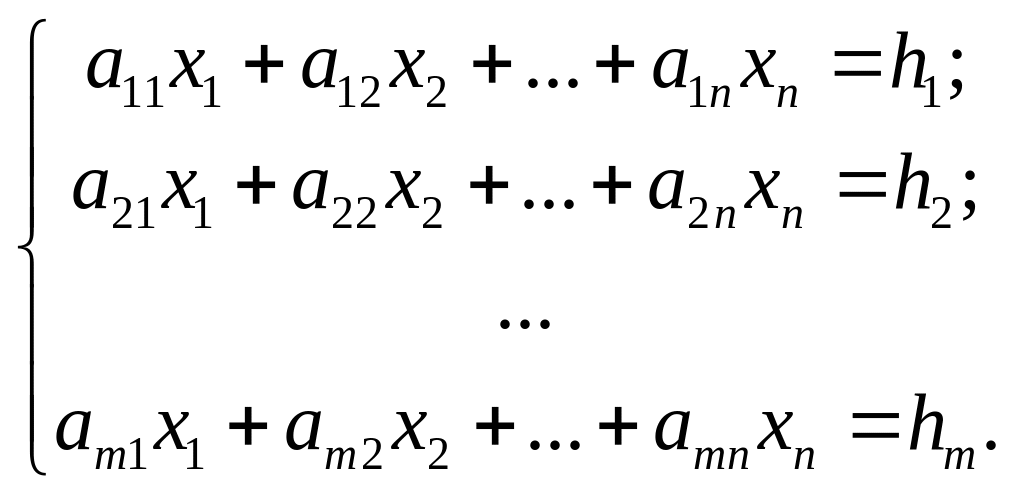
где - произвольные числа, - неизвестные величины.

Пример.

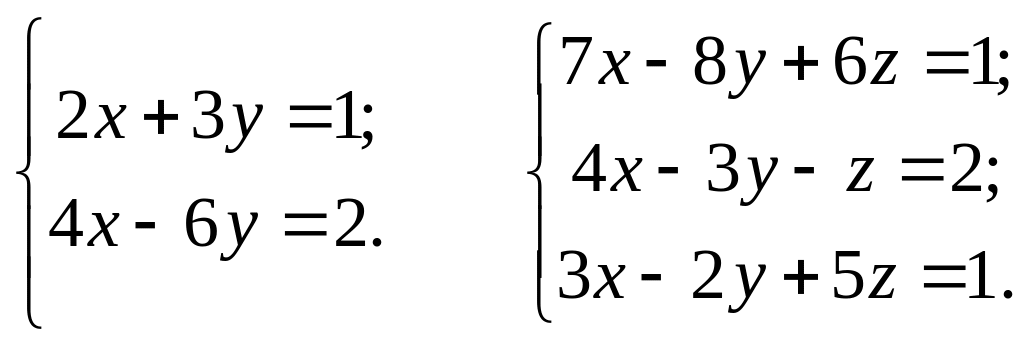
Решить систему - это значит найти все значения неизвестных, которые при подстановке в уравнения системы превращают их в правильные равенства (тождества). Система линейных уравнений может иметь одно решение, бесконечное множество решений или вообще не иметь решений.

При решении систем линейных уравнений можно использовать методы Гаусса, Крамера или метод обратной матрицы.

1.5. Метод обратной матрицы.

Систему линейных уравнений 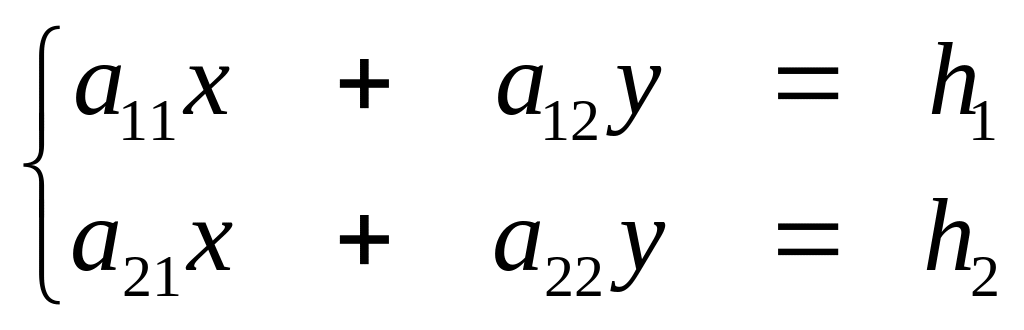можно записать в матричной форме 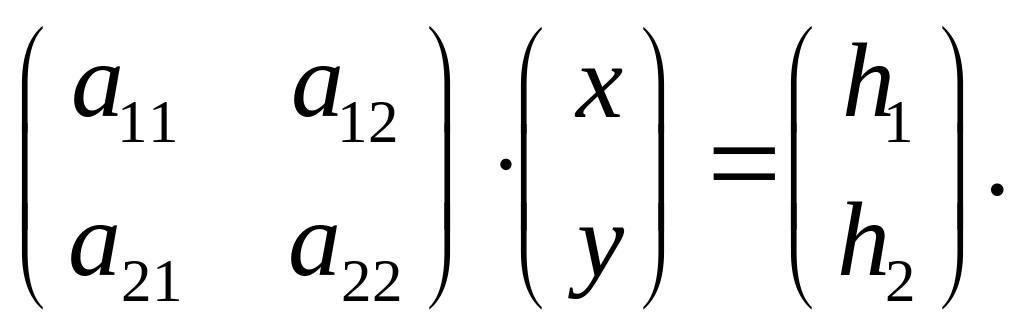Пусть 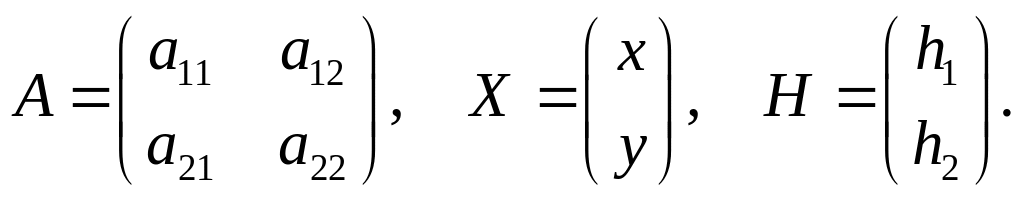Краткая запись данной системы имеет вид Чтобы решить систему умножим обе части уравнения на обратную матрицу . Тогда

Пример. Решить систему

Запишем эту систему в матричной форме Обратная матрица 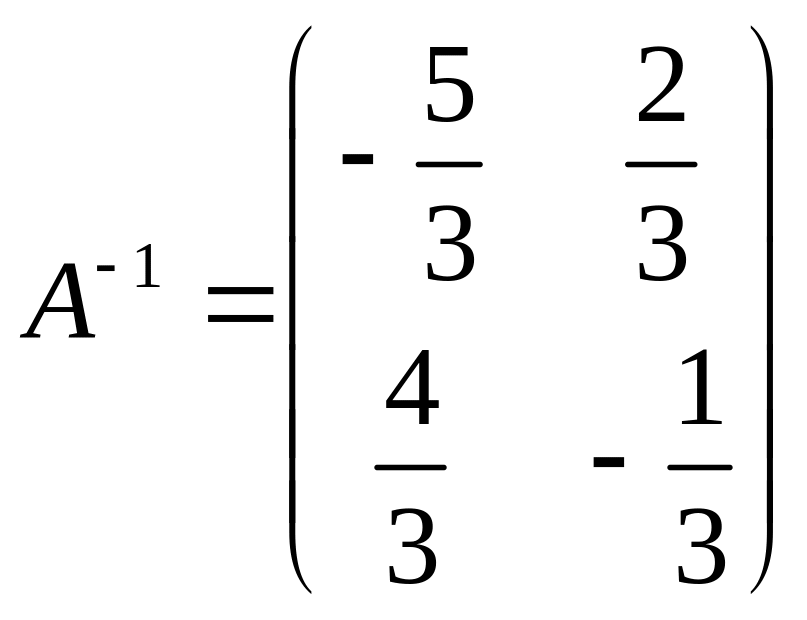была вычислена в одном из примеров выше. Тогда

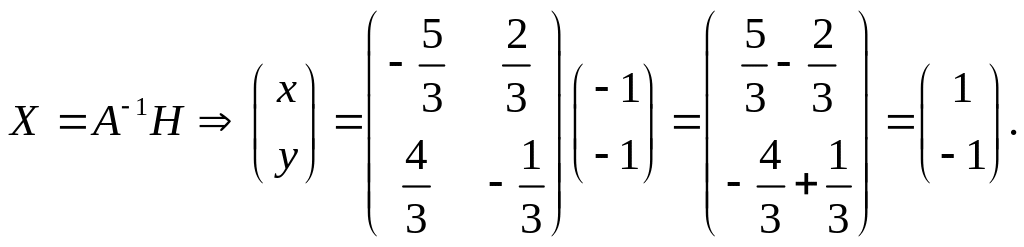
Ответ:

1.6.Метод Крамера.

Разберем этот метод решения на примере системы

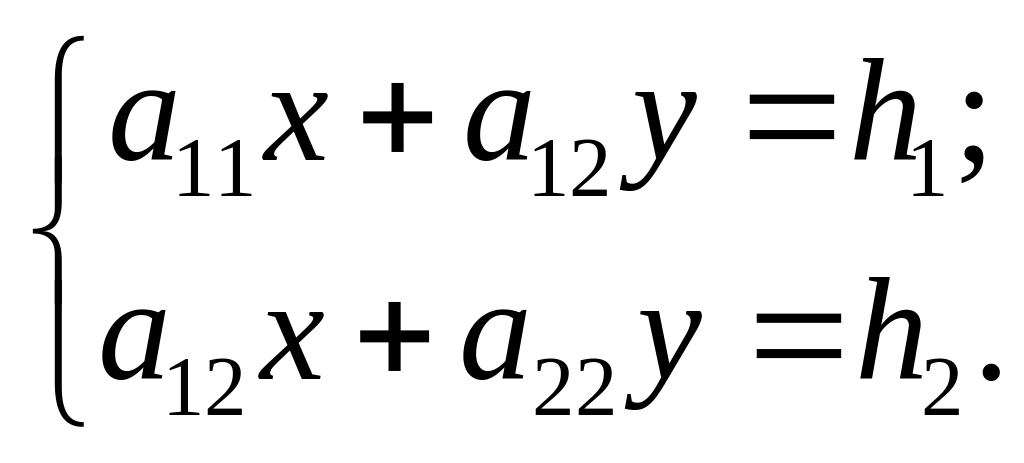
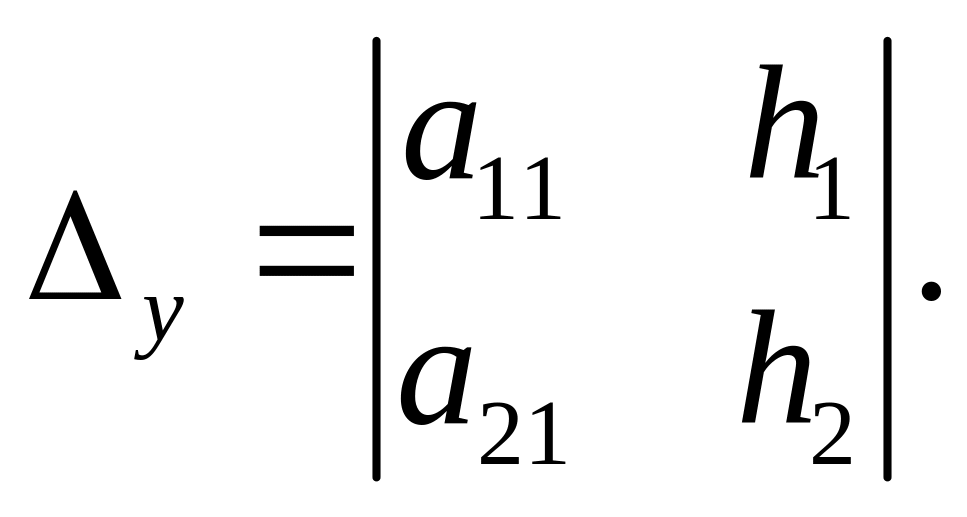Вычислим основной определитель системы и определители и Тогда Метод применим если основной определитель

Пример. Решить систему

Решение.

и

1.7.Решение систем линейных уравнений методом Гаусса.

Пример. Решить систему

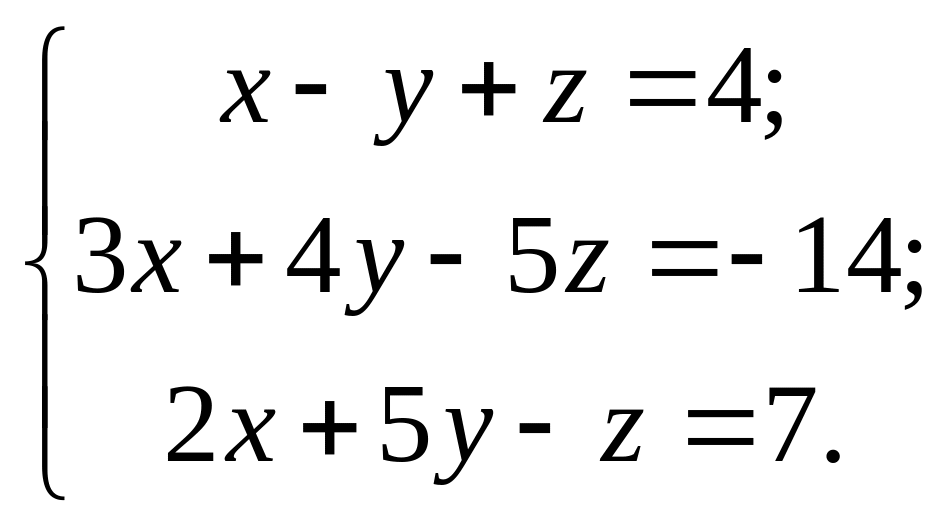
Решение. Запишем коэффициенты системы и правые части уравнений в матрицу, которая называется расширенной матрицей системы:

.

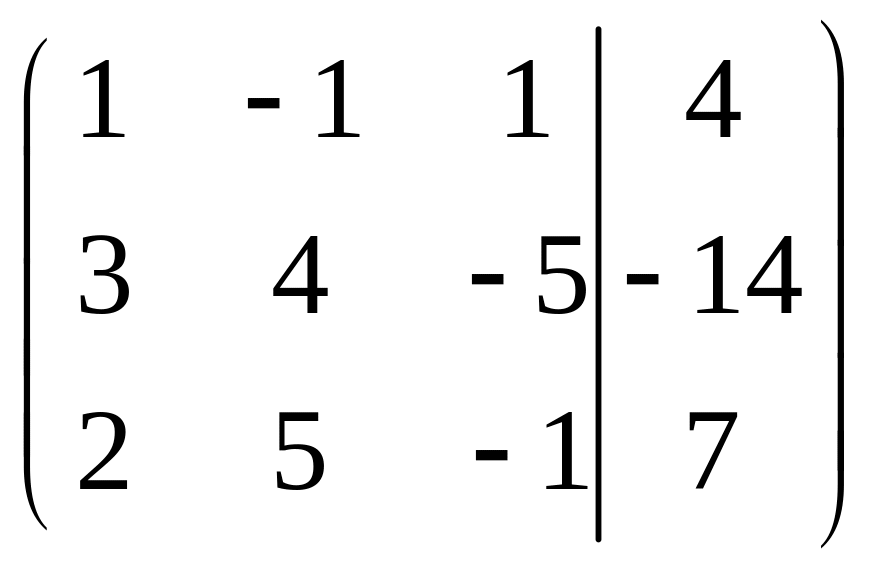Матрица, состоящая из коэффициентов при неизвестных, называется основной матрицей системы.

При решении системы можно прибавлять к строке расширенной матрицы другую строку, умноженную на какое-нибудь число. Мы стремимся получить нули во всех точках ниже диагонали основной матрицы.

.

Для этого ко второй строке прибавим первую, умноженную на (-3), а к третьей – первую умноженную на (-2).

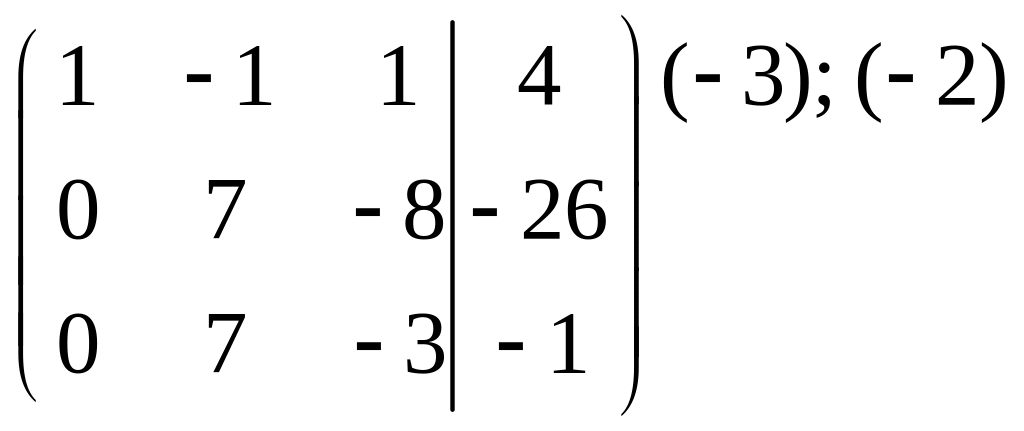
Нам осталось получить один ноль в третьей строке и втором столбце. Для этого прибавим к третьей строке вторую, умноженную на (-1).

.

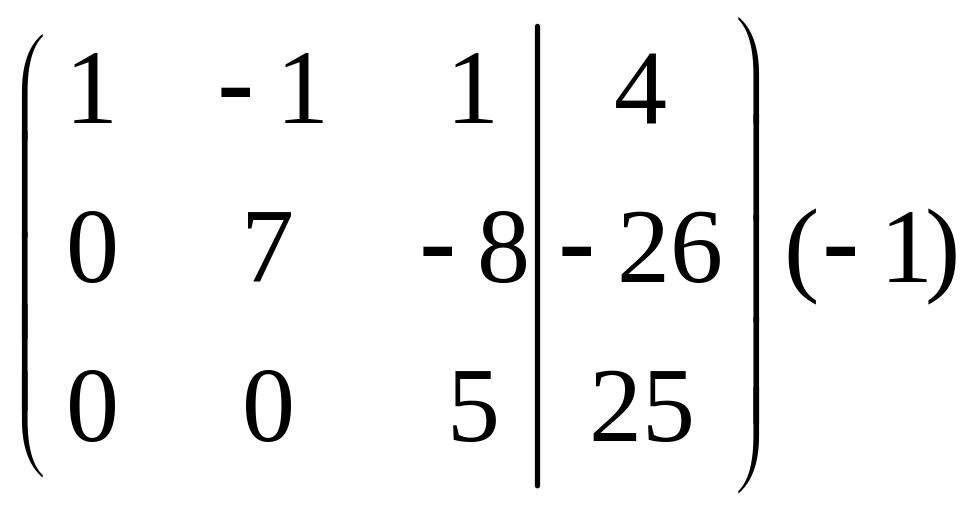Этой матрице соответствует система

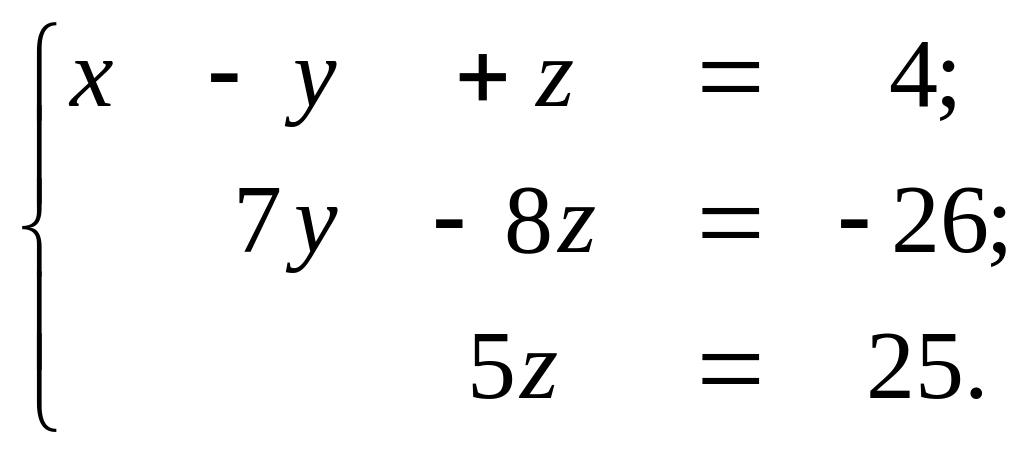
Из последнего уравнения Подставляем это значение во второе уравнение: Подставляем эти значения в первое уравнение

Ответ:

Пример 2. Решить систему

Записываем матрицы системы и преобразуем их

Число неизвестных больше, чем число уравнений, значит можно ожидать, что решений будет бесконечное множество или их вообще не будет. Сравним ранги основной и расширенной матриц. Любой минор третьего порядка содержит нулевую строку и поэтому равен нулю. С другой стороны существуют миноры второго порядка неравные нулю. Например, . Этот минор принадлежит обеим матрицам, поэтому ранги обоих матриц равны 2. По теореме Кронекера-Капелли система, в которой ранги основной и расширенной матриц совпадают должна иметь решения. Так как число неизвестных на единицу больше чем ранги обеих матриц, то система имеет бесконечное множество решений и одно из неизвестных можно положить свободным, а другие выразить через него. Например, пусть z - свободная переменная. Выразим y из второго уравнения: . Подставим эти значения в первое уравнение: .

Ответ: Система имеет множество решений. При любом значении z тройка чисел является решением системы.