2.5. Задания для самостоятельной работы по главе 2

2.1.

2.2.

2.3.

2.4. Доказать, что для равенства нулю определителя второго порядка необходимо и достаточно, чтобы его строки были пропорциональны. То же верно и для столбцов (если некоторые элементы определителя равны нулю, то пропорциональность можно понимать в том смысле, что элементы одной строки получаются из соответствующих элементов другой строки умножением на одно и то же число, быть может, равное нулю).

2.5.

2.6. Показать, что значение дроби , где по крайней мере одно из чисел с или d отлично от нуля, тогда и только тогда не зависит от значения х, когда

2.7. Найти наибольшее значение, которое может принимать определитель 3-го порядка, при условии, что все его элементы равны 1 или (-1).

2.8. Найти наибольшее значение, которое может принимать определитель 3-го порядка, при условии, что все его элементы равны 1 или 0.

2.9. Доказать, что от любой перестановки чисел 1,2,…,n, содержащей k инверсий, можно перейти к исходному положению путем k смежных транспозиций, но нельзя перейти путем меньшего числа таких транспозиций.

2.10. Выбрать значения i и k так, чтобы произведение входило в определитель 6-го порядка со знаком минус.

2.11. Вычислить определитель

,

в котором все элементы по одну сторону от главной диагонали равны нулю.

2.12. Решить уравнение

2.13. Доказать, что определитель не изменится, если к каждому столбцу, начиная со второго, прибавить предыдущий столбец.

2.14. Разлагая по 3-ей строке, вычислить определитель

2.15. Вычислить определитель

Глава 3. Алгебра матриц (продолжение)

3.1 Обратная матрица

Пусть задана квадратная матрица порядка n.

Определение. Квадратная матрица А^-1 порядка n называется обратной к матрице А, если она удовлетворяет соотношению

(3.1.1)

Присоединенной матрицей квадратной матрицы А называется матрица А*, каждый элемент которой есть алгебраическое дополнение элемента транспонированной матрицы А, т.е.

.

Квадратная матрица А называется невырожденной (неособенной), если ее определитель |A| отличен от нуля, и вырожденной, если |A|=0.

Теорема. Для всякой невырожденной матрицы А существует единственная обратная матрица А^-1, определяемая следующим выражением:

(3.1.2)

Доказательство. Докажем сначала единственность. Предположим, что существуют две различные обратные матрицы и . Тогда имеем

	(3.1.3)
	(3.1.4)

Из двух последних равенств следует, что = .

Покажем теперь, что выражение (3.1.2) действительно задает обратную матрицу. Составим произведение АА^*. Очевидно, что элементами данного произведения являются суммы произведений элементов строк матрицы А на алгебраические дополнения, т.е. . Как известно из гл.2, при i=j =0. В итоге получаем

,

или ,

откуда .

В заключение отметим, что А^* перестановочна с А, т.е. , что видно непосредственно. Теорема доказана.

Пример. Вычислить обратную матрицу для матрицы А, равной:

.

Решение. . Вычислим присоединенную матрицу А^*:

А₁₁=-3, А₁₂=-1, А₂₁=-1, А₂₂=2,

; .

Проверкой убеждаемся, что АА^-1=Е.

Обратная матрица обладает следующими свойствами:

1. Определитель обратной матрицы равен обратной величине определителя исходной матрицы, т.е. |A^-1|= .

2. Произведение двух невырожденных матриц А и В является невырожденной матрицей и .

3. Если матрица А невырожденная, то .

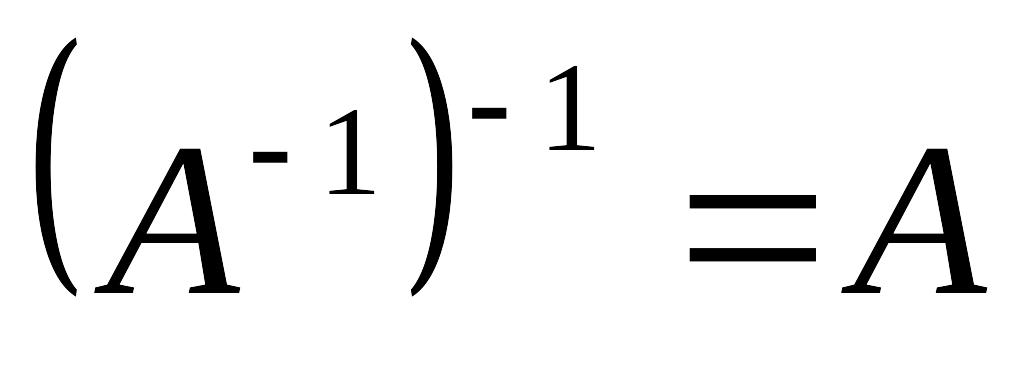4. Обратная матрица к транспонированной является транспонированной матрицей к обратной, т.е. .